Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-22T23:48:52.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on the limitations of the Theodorsen and Sears functions

Published online by Cambridge University Press:  07 December 2016

Ulrike Cordes ,
G. Kampers ,
T. Meißner ,
C. Tropea ,
J. Peinke  and
M. Hölling
Ulrike Cordes*
Affiliation:
Institute for Fluid Mechanics and Aerodynamics, Technische Universität Darmstadt, Flughafenstraße 19, 64347 Griesheim, Germany
G. Kampers
Affiliation:
ForWind, Institute of Physics, University of Oldenburg, 26111 Oldenburg, Germany
T. Meißner
Affiliation:
Institute for Fluid Mechanics and Aerodynamics, Technische Universität Darmstadt, Flughafenstraße 19, 64347 Griesheim, Germany
C. Tropea
Affiliation:
Institute for Fluid Mechanics and Aerodynamics, Technische Universität Darmstadt, Flughafenstraße 19, 64347 Griesheim, Germany
J. Peinke
Affiliation:
ForWind, Institute of Physics, University of Oldenburg, 26111 Oldenburg, Germany
M. Hölling
Affiliation:
ForWind, Institute of Physics, University of Oldenburg, 26111 Oldenburg, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Two transfer functions for the unsteady lift response of an airfoil under attached flow conditions are experimentally investigated: the Theodorsen function for an airfoil oscillating in a constant free stream and the Sears function for a steady airfoil encountering a sinusoidal vertical gust. A two-dimensional airfoil with a Clark Y profile is submitted to two different unsteady excitations of distinct frequencies: a pitching oscillation around the leading edge and a sinusoidal vertical gust. 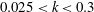The reduced frequency of the perturbation is in the range of $0.025<k<0.3$ and the Reynolds number of the undisturbed flow is in the range of 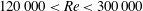$120\,000<\mathit{Re}<300\,000$. While the Theodorsen function is found to be a good estimator for the unsteady lift at moderate mean angles of attack, the Sears function does not capture the experimental transfer functions in frequency dependence or in limiting values. A second-order model provided by Atassi (J. Fluid Mech., vol. 141, 1984, pp. 109–122) agrees well with the experimental transfer function.

JFM classification

Aerodynamics: Aerodynamics
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 811 , 25 January 2017 , R1
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atassi, H. M. 1984 The Sears problem for a lifting airfoil revisited – new results. J. Fluid Mech. 141, 109–122.CrossRefGoogle Scholar
Bratt, J. B. 1945 The effect of mean incidence, amplitude of oscillation, profile and aspect ratio on pitching moment derivatives. Rep. Memoranda 2064, 2299–2348.Google Scholar
Cordes, U.2016 Experimental investigation of a passively deforming airfoil under dynamic flow conditions. PhD thesis, Technische Universität Darmstadt.Google Scholar
Dowell, E. 2014 A Modern Course in Aeroelasticity, vol. 217. Springer.Google Scholar
Gaunaa, M. & Andersen, P. B. 2009 Load reduction using pressure difference on airfoil for control of trailing edge flaps. In 2009 European Wind Energy Conference and Exhibition, European Wind Energy Assosciation.Google Scholar
Goldstein, M. E. & Atassi, H. M. 1976 A complete second-order theory for the unsteady flow about an airfoil due to a periodic gust. J. Fluid Mech. 74 (04), 741–765.CrossRefGoogle Scholar
Halfman, R. L.1952 Experimental aerodynamic derivatives of a sinusoidally oscillating airfoil in two-dimensional flow. NACA Tech. Rep. 1108.Google Scholar
Hatanaka, A. & Tanaka, H. 2002 New estimation method of aerodynamic admittance function. J. Wind Engng Ind. Aerodyn. 90 (12), 2073–2086.CrossRefGoogle Scholar
Knebel, P., Kittel, A. & Peinke, J. 2011 Atmospheric wind field conditions generated by active grids. Exp. Fluids 51, 471–481.CrossRefGoogle Scholar
Larose, G. L. 1999 Experimental determination of the aerodynamic admittance of a bridge deck segment. J. Fluids Struct. 13 (7), 1029–1040.CrossRefGoogle Scholar
Mateescu, D. & Abdo, M.2003 Unsteady aerodynamic solutions for oscillating airfoils. AIAA Paper 227, 2003.Google Scholar
Rainey, A. G.1957 Measurement of aerodynamic forces for various mean angles of attack on an airfoil oscillating in pitch and on two finite-span wings oscillating in bending with emphasis on damping in the stall. NACA Tech Rep. 1305.Google Scholar
Reid, E. G. 1940 An experimental determination of the lift of an oscillating airfoil. J. Aero. Sci. 8 (1), 1–6.Google Scholar
Sears, W. R.1938 A systematic presentation of the theory of thin airfoils in non-uniform motion. PhD thesis, California Institute of Technology.Google Scholar
Silverstein, A. & Joyner, U. T.1939 Experimental verification of the theory of oscillating airfoils. NACA Tech. Rep. 673.Google Scholar
Theodorsen, T.1935 General theory of aerodynamic instability and the mechanism of flutter. NACA Rep. 496, US National Advisory Committee for Aeronautics, Langley, VA 13.Google Scholar