Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-12-01T04:53:34.280Z Has data issue: false hasContentIssue false
  • English
  • Français

The non-stationary hysteresis phenomenon in shock wave reflections

Published online by Cambridge University Press:  02 September 2013

Meital Geva ,
Omri Ram  and
Oren Sadot
Meital Geva
Affiliation:
Pearlstone Center for Aeronautical Engineering Studies, Department of Mechanical Engineering, Faculty of Engineering Sciences, Ben-Gurion University of the Negev, Beer Sheva, 84105, Israel
Omri Ram
Affiliation:
Pearlstone Center for Aeronautical Engineering Studies, Department of Mechanical Engineering, Faculty of Engineering Sciences, Ben-Gurion University of the Negev, Beer Sheva, 84105, Israel
Oren Sadot*
Affiliation:
Pearlstone Center for Aeronautical Engineering Studies, Department of Mechanical Engineering, Faculty of Engineering Sciences, Ben-Gurion University of the Negev, Beer Sheva, 84105, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The non-stationary transition from Mach to regular reflection followed by a reverse transition from regular to Mach reflection is investigated experimentally. A new experimental setup in which an incident shock wave reflects from a cylindrical concave surface followed by a cylindrical convex surface of the same radius is introduced. Unlike other studies that indicate problems in identifying the triple point, an in-house image processing program, which enables automatic detection of the triple point, is developed and presented. The experiments are performed in air having a specific heats ratio 1.4 at three different incident-shock-wave Mach numbers: 1.2, 1.3 and 1.4. The data are extracted from high-resolution schlieren images obtained by means of a fully automatically operated shock-tube system. Each experiment produces a single image. However, the high accuracy and repeatability of the control system together with the fast opening valve enables us to monitor the dynamic evolution of the shock reflections. Consequently, high-resolution results both in space and time are obtained. The credibility of the present analysis is demonstrated by comparing the first transition from Mach to regular reflection (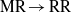$\mathrm{MR} \rightarrow \mathrm{RR} $) with previous single cylindrical concave surface experiments. It is found that the second transition, back to Mach reflection (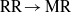$\mathrm{RR} \rightarrow \mathrm{MR} $), occurs earlier than one would expect when the shock reflects from a single cylindrical convex surface. Furthermore, the hysteresis is observed at incident-shock-wave Mach numbers smaller than those at which the dual-solution domain starts, which is the minimal value for obtaining hysteresis in steady and pseudo-steady flows. The existence of a non-stationary hysteresis phenomenon, which is different from the steady-state hysteresis phenomenon, is discovered.

JFM classification

Compressible Flows: Compressible Flows Compressible Flows: Shock waves
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 732 , 10 October 2013 , R1
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ben-Dor, G. 2007 Shock Wave Reflection Phenomena, 2nd edn. Springer.Google Scholar
Ben-Dor, G., Ivanov, M., Vasilev, E. I. & Elperin, T. 2002 Hysteresis processes in the regular reflection $\leftrightarrow $ Mach reflection transition in steady flows. Prog. Aero. Sci. 38 (4–5), 347–387.CrossRefGoogle Scholar
Ben-Dor, G. & Takayama, K. 1985 Analytical prediction of the transition from Mach to regular reflection over cylindrical concave wedges. J. Fluid Mech. 158, 365–380.CrossRefGoogle Scholar
Ben-Dor, G. & Takayama, K. 1986/7 The dynamics of the transition from Mach to regular reflection over concave cylinders. Israel J. Tech. 23, 71–74.Google Scholar
Ben-Dor, G., Takayama, K. & Dewey, J. M. 1987 Further analytical considerations of the reflection of weak shock waves over a concave wedge. Fluid Dyn. Res. 2, 77–85.CrossRefGoogle Scholar
Felthun, L. T. & Skews, B. W. 2004 Dynamic shock wave reflection. AIAA J. 42 (8), 1633–1639.CrossRefGoogle Scholar
Gruber, S. 2012 Weak shock wave reflections from concave curved surfaces. M.Sc thesis, University of Witwatersrand, Johannesburg, South Africa.Google Scholar
Gruber, S. & Skews, B. W. 2013 Weak shock wave reflection from concave surfaces. Exp. Fluids 54 (7), 1–14.CrossRefGoogle Scholar
Hornung, H. G., Oretel, H. & Sanderman, R. J. 1979 Transition to Mach reflection of shock waves in steady and pseudosteady flow with and without relaxation. J. Fluid Mech. 90, 541–560.CrossRefGoogle Scholar
Itoh, S., Okazaki, N. & Itaya, M. 1981 On the transition between regular and Mach reflection in truly non-stationary flows. J. Fluid Mech. 108, 383–400.CrossRefGoogle Scholar
Molder, S. 1979 Particular conditions for the termination of regular reflection of shock waves. CASI Trans. 25, 44–49.Google Scholar
Naidoo, K. 2011 Dynamic shock wave reflection phenomena. PhD thesis, University of Witwatersrand, Johannesburg, South Africa.Google Scholar
Naidoo, K. & Skews, B. W. 2011 Dynamic effects on the transition between two-dimensional regular and Mach reflection of shock waves in an ideal, steady supersonic free stream. J. Fluid Mech. 676, 432–460.CrossRefGoogle Scholar
Skews, B. W. & Blitterswijk, A. 2011 Shock wave reflection off coupled surfaces. Shock Waves 21, 491–498.CrossRefGoogle Scholar
Skews, B. W. & Kleine, H. 2007 Flow features resulting from shock wave impact on a cylindrical cavity. J. Fluid Mech. 580, 481–493.CrossRefGoogle Scholar
Skews, B. W. & Kleine, H. 2009 Unsteady flow diagnostics using weak perturbations. Exp. Fluids 46, 65–76.CrossRefGoogle Scholar
Skews, B. W. & Kleine, H. 2010 Shock wave interaction with convex circular cylindrical surfaces. J. Fluid Mech. 654, 195–205.CrossRefGoogle Scholar
Takayama, K. & Ben-Dor, G. 1989 A reconsideration of the transition criterion from Mach to regular reflection over cylindrical concave surfaces. Korean Soc. Mech. Engrs J. 3, 6–9.Google Scholar
Takayama, K. & Sasaki, M. 1983 Effects of radius of curvature and initial angle on the shock transition over concave and convex walls. Rept. Inst. High-Speed Mech., Tohoku University, Sendai, Japan 46, 1–30.Google Scholar