Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-08T21:56:43.839Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-modal analysis of coaxial jets

Published online by Cambridge University Press:  13 June 2019

D. Montagnani  and
F. Auteri Open the ORCID record for F. Auteri [Opens in a new window]
D. Montagnani
Affiliation:
Dipartimento di Scienze e Tecnologie Aerospaziali, Politecnico di Milano, via La Masa 34, 20156 Milano, Italy
F. Auteri*
Affiliation:
Dipartimento di Scienze e Tecnologie Aerospaziali, Politecnico di Milano, via La Masa 34, 20156 Milano, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

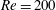In this work, we investigate the subcritical behaviour of a coaxial jet subject to small-amplitude perturbations at the inflow. We use the results of optimal harmonic analysis and dynamic-mode decomposition (DMD) of the flow fields at a Reynolds number, based on the diameter and maximum velocity of the inner inlet pipe, of $Re=200$, to show that, for a sufficiently low value of the Reynolds number, the coherent structures appearing in the perturbed dynamics of the nonlinear system can be effectively described in terms of the harmonic response of the flow. We also show that, for larger subcritical values of the Reynolds number, 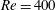$Re=400$, a huge amplification of disturbances quickly makes nonlinear effects relevant. Large-scale, near-field coherent dynamics can be still interpreted as an evidence of the preferred response of the system, using DMD of the flow to describe the noise-driven transition to turbulence downstream. The influence of the axial velocity ratio and the rotational motion of the outer stream are assessed as well. Harmonic analysis successfully predicts the prevalence of rotating helical structures observed in the columnar flow for moderate swirl of the outer jet. Finally, we compare the receptivity of the nonlinear system to the optimal linear perturbations with its response to stochastic forcing. Optimal forcing is still more effective than white noise in driving the system to a turbulent state, where nonlinear dynamics prevails. We still conclude that linear optimal forcing may be relevant in investigating the transition to turbulence in coaxial jets, even if more about the transition process could be learnt from a more expensive nonlinear analysis.

JFM classification

Instability: Absolute/convective instability Wakes/Jets: Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 872 , 10 August 2019 , pp. 665 - 696
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balarac, G. & Métais, O. 2005 The near field of coaxial jets: a numerical study. Phys. Fluids 17 (6), 065102.Google Scholar
Balarac, G., Métais, O. & Lesieur, M. 2007 Mixing enhancement in coaxial jets through inflow forcing: a numerical study. Phys. Fluids 19 (7), 075102.Google Scholar
Batchelor, G. K. & Gill, A. E. 1962 Analysis of the stability of axisymmetric jets. J. Fluid Mech. 14 (4), 529–551.Google Scholar
Billant, P. & Gallaire, F. 2013 A unified criterion for the centrifugal instabilities of vortices and swirling jets. J. Fluid Mech. 734, 5–35.Google Scholar
Blackburn, H. M., Barkley, D. & Sherwin, S. J. 2008a Convective instability and transient growth in flow over a backward-facing step. J. Fluid Mech. 603, 271–304.Google Scholar
Blackburn, H. M., Sherwin, S. J. & Barkley, D. 2008b Convective instability and transient growth in steady and pulsatile stenotic flows. J. Fluid Mech. 607, 267–277.Google Scholar
Boujo, E. & Gallaire, F. 2015 Sensitivity and open-loop control of stochastic response in a noise amplifier flow: the backward-facing step. J. Fluid Mech. 762, 361–392.Google Scholar
Brancher, P., Chomaz, J. M. & Huerre, P. 1994 Direct numerical simulations of round jets: vortex induction and side jets. Phys. Fluids 6 (5), 1768–1774.Google Scholar
Buresti, G., Talamelli, A. & Petagna, P. 1994 Experimental characterization of the velocity field of a coaxial jet configuration. Exp. Therm. Fluid Sci. 9 (2), 135–146.Google Scholar
Canton, J., Auteri, F. & Carini, M. 2017 Linear global stability of two incompressible coaxial jets. J. Fluid Mech. 824, 886–911.Google Scholar
Cantwell, C. D., Barkley, D. & Blackburn, H. M. 2010 Transient growth analysis of flow through a sudden expansion in a circular pipe. Phys. Fluids 22 (3), 034101.Google Scholar
Champagne, F. H. & Kromat, S. 2000 Experiments on the formation of a recirculation zone in swirling coaxial jets. Exp. Fluids 29 (5), 494–504.Google Scholar
Champagne, F. H. & Wygnanski, I. J. 1971 An experimental investigation of coaxial turbulent jets. Intl J. Heat Mass Transfer 14 (9), 1445–1464.Google Scholar
Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 156, 209–240.Google Scholar
Cohen, J. & Wygnanski, I. 1987 The evolution of instabilities in the axisymmetric jet. Part 1. The linear growth of disturbances near the nozzle. J. Fluid Mech. 176, 191–219.Google Scholar
Crighton, D. G. & Gaster, M. 1976 Stability of slowly diverging jet flow. J. Fluid Mech. 77 (2), 397–413.Google Scholar
Dahm, W. J. A., Frieler, C. E. & Tryggvason, G. 1992 Vortex structure and dynamics in the near field of a coaxial jet. J. Fluid Mech. 241, 371–402.Google Scholar
Danaila, I., Dus̆ek, J. & Anselmet, F. 1997 Coherent structures in a round, spatially evolving, unforced, homogeneous jet at low Reynolds numbers. Phys. Fluids 9 (11), 3323–3342.Google Scholar
Delbende, I. & Rossi, M. 2005 Nonlinear evolution of a swirling jet instability. Phys. Fluids 17 (4), 044103.Google Scholar
Dussin, D., Fossati, M., Guardone, A. & Vigevano, L. 2009 Hybrid grid generation for two-dimensional high-Reynolds flows. Comput. Fluids 38 (10), 1863–1875.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1996 Generalized stability theory. Part I. Autonomous operators. J. Atmos. Sci. 53 (14), 2025–2040.Google Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G.2008 nek5000 web page. http://nek5000.mcs.anl.gov.Google Scholar
Gallaire, F. & Chomaz, J.-M. 2003a Instability mechanisms in swirling flows. Phys. Fluids 15 (9), 2622–2639.Google Scholar
Gallaire, F. & Chomaz, J.-M. 2003b Mode selection in swirling jet experiments: a linear stability analysis. J. Fluid Mech. 494, 223–253.Google Scholar
Garnaud, X., Lesshafft, L., Schmid, P. J. & Huerre, P. 2013a Modal and transient dynamics of jet flows. Phys. Fluids 25 (4), 044103.Google Scholar
Garnaud, X., Lesshafft, L., Schmid, P. J. & Huerre, P. 2013b The preferred mode of incompressible jets: linear frequency response analysis. J. Fluid Mech. 716, 189–202.Google Scholar
Gohil, T. B., Saha, A. K. & Muralidhar, K. 2012 Numerical study of instability mechanisms in a circular jet at low Reynolds numbers. Comput. Fluids 64, 1–18.Google Scholar
Jeun, J., Nichols, J. W. & Jovanovi, M. R. 2016 Input-output analysis of high-speed axisymmetric isothermal jet noise. Phys. Fluids 28 (4), 047101.Google Scholar
Khorrami, M. R. 1991 On the viscous modes of instability of a trailing line vortex. J. Fluid Mech. 225, 197–212.Google Scholar
Lefebvre, A. H. 1998 Gas Turbine Combustion. CRC Press.Google Scholar
Leibovich, S. & Stewartson, K. 1983 A sufficient condition for the instability of columnar vortices. J. Fluid Mech. 126, 335–356.Google Scholar
Lesshafft, L., Semeraro, O., Jaunet, V., Cavalieri, A. V. & Jordan, P.2018 Resolvent-based modelling of coherent wavepackets in a turbulent jet. arXiv:1810.09340.Google Scholar
Liang, H. & Maxworthy, T. 2005 An experimental investigation of swirling jets. J. Fluid Mech. 525, 115–159.Google Scholar
Liepmann, D. & Gharib, M. 1992 The role of streamwise vorticity in the near-field entrainment of round jets. J. Fluid Mech. 245, 643–668.Google Scholar
Loiseleux, T. & Chomaz, J.-M. 2003 Breaking of rotational symmetry in a swirling jet experiment. Phys. Fluids 15 (2), 511–523.Google Scholar
Loiseleux, T., Chomaz, J.-M. & Huerre, P. 1998 The effect of swirl on jets and wakes: linear instability of the rankine vortex with axial flow. Phys. Fluids 10 (5), 1120–1134.Google Scholar
Loiseleux, T., Delbende, I. & Huerre, P. 2000 Absolute and convective instabilities of a swirling jet/wake shear layer. Phys. Fluids 12 (2), 375–380.Google Scholar
Mantic̆-Lugo, V. & Gallaire, F. 2016 Self-consistent model for the saturation mechanism of the response to harmonic forcing in the backward-facing step flow. J. Fluid Mech. 793, 777–797.Google Scholar
Martin, J. E. & Meiburg, E. 1994 On the stability of the swirling jet shear layer. Phys. Fluids 6 (1), 424–426.Google Scholar
Martin, J. E. & Meiburg, E. 1996 Nonlinear axisymmetric and three-dimensional vorticity dynamics in a swirling jet model. Phys. Fluids 8 (7), 1917–1928.Google Scholar
Mattingly, G. E. & Chang, C. C. 1974 Unstable waves on an axisymmetric jet column. J. Fluid Mech. 65 (3), 541–560.Google Scholar
Michalke, A. 1999 Absolute inviscid instability of a ring jet with back-flow and swirl. Eur. J. Mech. (B/Fluids) 18 (1), 3–12.Google Scholar
Morris, P. J. 1976 The spatial viscous instability of axisymmetric jets. J. Fluid Mech. 77, 511–529.Google Scholar
Örlü, R. & Alfredsson, P. H. 2008 An experimental study of the near-field mixing characteristics of a swirling jet. Flow Turbul. Combust. 80 (3), 323–350.Google Scholar
Reddy, S. C. & Henningson, D. S. 1993 Energy growth in viscous channel flows. J. Fluid Mech. 252, 209–238.Google Scholar
Rehab, H., Villermaux, E. & Hopfinger, E. J. 1997 Flow regimes of large-velocity-ratio coaxial jets. J. Fluid Mech. 345, 357–381.Google Scholar
Reynolds, A. J. 1962 Observations of a liquid-into-liquid jet. J. Fluid Mech. 14 (4), 552–556.Google Scholar
Ribeiro, M. M. & Whitelaw, J. H. 1980 Coaxial jets with and without swirl. J. Fluid Mech. 96 (4), 769–795.Google Scholar
Rowley, C. W., Mezi, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.Google Scholar
Sadr, R. & Klewicki, J. C. 2003 An experimental investigation of the near-field flow development in coaxial jets. Phys. Fluids 15 (5), 1233–1246.Google Scholar
Saiki, Y., Suzuki, Y. & Kasagi, N. 2011 Active control of swirling coaxial jet mixing with manipulation of large-scale vortical structures. Flow Turbul. Combust. 86 (3-4), 399–418.Google Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39 (1), 129–162.Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.Google Scholar
Schmidt, O. T., Towne, A., Rigas, G., Colonius, T. & Brès, G. A. 2018 Spectral analysis of jet turbulence. J. Fluid Mech. 855, 953–982.Google Scholar
Schumaker, S. A. & Driscoll, J. F. 2012 Mixing properties of coaxial jets with large velocity ratios and large inverse density ratios. Phys. Fluids 24, 055101.Google Scholar
Segalini, A. & Talamelli, A. 2011 Experimental analysis of dominant instabilities in coaxial jets. Phys. Fluids 23 (2), 024103.Google Scholar
Semeraro, O., Jaunet, V., Jordan, P., Cavalieri, A. V. & Lesshafft, L. 2016 Stochastic and harmonic optimal forcing in subsonic jets. In 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France.Google Scholar
da Silva, C. B., Balarac, G. & Métais, O. 2003 Transition in high velocity ratio coaxial jets analysed from direct numerical simulations. J. Turbul. 4, N24.Google Scholar
Talamelli, A. & Gavarini, I. 2006 Linear instability characteristics of incompressible coaxial jets. Flow Turbul. Combust. 76 (3), 221–240.Google Scholar
Tang, S. K. & Ko, N. W. M. 1994 Coherent structure interactions in an unexcited coaxial jet. Exp. Fluids 17 (3), 147–157.Google Scholar
Villermaux, E. & Rehab, H. 2000 Mixing in coaxial jets. J. Fluid Mech. 425, 161–185.Google Scholar
Weller-Calvo, J., Fontane, J. & Joly, L. 2015 Mode selection in swirling coaxial jets. In Proceedings of Sixth International Symposium on Bifurcations and Instabilities in Fluid Dynamics (BIFD 2015), 15 July 2015–17 July 2015 (Paris, France).Google Scholar
Weller-Calvo, J., Joly, L. & Fontane, J. 2013 Stability of coaxial swirling jets. In 66th Annual Meeting of the American Physical Society’s Division of Fluid Dynamics (DFD), 24 November 2013. American Physical Society.Google Scholar
Wicker, R. B. & Eaton, J. K. 1994 Near field of a coaxial jet with and without axial excitation. AIAA J. 32 (3), 542–546.Google Scholar
Williams, T. J., Ali, M. R. M. H. & Anderson, J. S. 1969 Noise and flow characteristics of coaxial jets. J. Mech. Engng Sci. 11 (2), 133–142.Google Scholar