Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T12:42:17.435Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear evolution of the zigzag instability in stratified fluids: a shortcut on the route to dissipation

Published online by Cambridge University Press:  06 March 2008

AXEL DELONCLE ,
PAUL BILLANT  and
JEAN-MARC CHOMAZ
AXEL DELONCLE
Affiliation:
LadHyX, CNRS, Ecole Polytechnique, 91128 Palaiseau Cedex, [email protected]
PAUL BILLANT
Affiliation:
LadHyX, CNRS, Ecole Polytechnique, 91128 Palaiseau Cedex, [email protected]
JEAN-MARC CHOMAZ
Affiliation:
LadHyX, CNRS, Ecole Polytechnique, 91128 Palaiseau Cedex, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present high-resolution direct numerical simulations of the nonlinear evolution of a pair of counter-rotating vertical vortices in a stratified fluid for various high Reynolds numbers Re and low Froude numbers Fh. The vortices are bent by the zigzag instability producing high vertical shear. There is no nonlinear saturation so that the exponential growth is stopped only when the viscous dissipation by vertical shear is of the same order as the horizontal transport, i.e. 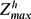when /Re=O(1) where 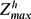is the maximum horizontal enstrophy non-dimensionalized by the vortex turnover frequency. The zigzag instability therefore directly transfers the energy from large scales to the small dissipative vertical scales. However, for high Reynolds number, the vertical shear created by the zigzag instability is so intense that the minimum local Richardson number Ri decreases below a threshold of around 1/4 and small-scale Kelvin–Helmholtz instabilities develop. We show that this can only occur when 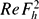is above a threshold estimated as 340. Movies are available with the online version of the paper.

JFM classification

Vortex Flows: Vortex instability Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 599 , 25 March 2008 , pp. 229 - 239
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Billant, P. & Chomaz, J.-M. 2000 a Experimental evidence for a new instability of a vertical columnar vortex pair in a strongly stratified fluid. J. Fluid Mech. 418, 167–188.Google Scholar
Billant, P. & Chomaz, J.-M. 2000 b Theoretical analysis of the zigzag instability of a vertical columnar vortex pair in a strongly stratified fluid. J. Fluid Mech. 419, 29–63.Google Scholar
Billant, P. & Chomaz, J. M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 13, 1645–1651.Google Scholar
Billant, P., Dritschel, D. G. & Chomaz, J.-M. 2006 Bending and twisting instabilities of columnar elliptical vortices in a rotating strongly stratified fluid. J. Fluid Mech. 561, 73–102.Google Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.Google Scholar
Deloncle, A., Billant, P. & Chomaz, J.-M. 2008 Three-dimensional stability of vortex arrays in a stratified and rotating fluid: theoretical analysis. J. Fluid Mech. (to be submitted).Google Scholar
Gill, A. E. 1982 Atmosphere-Ocean Dynamics. Academic.Google Scholar
Howard, L. N. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 10, 509–512.CrossRefGoogle Scholar
Laval, J.-P. McWilliams, J. C. & Dubrulle, B. 2003 Forced stratified turbulence: successive transitions with Reynolds number. Phys. Rev. E 68, 036308.Google Scholar
Lilly, D. K. 1983 Stratified turbulence and the mesoscale variability of the atmosphere. J. Atmos. Sci. 40, 749–761.2.0.CO;2>CrossRefGoogle Scholar
Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid Mech. 550, 207–242.Google Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508.CrossRefGoogle Scholar
Otheguy, P., Chomaz, J.-M. & Billant, P. 2006 Elliptic and zigzag instabilities on co-rotating vertical vortices in a stratified fluid. J. Fluid Mech. 553, 253–272.Google Scholar
Riley, J. J. & deBruynKops, S. M. 2003 Dynamics of turbulence strongly influenced by buoyancy. J. Fluid Mech. 15, 2047–2059.Google Scholar
Sipp, D., Jacquin, L. & Cossu, C. 2000 Self-adaptation and viscous selection in concentrated two-dimensional vortex dipoles. Phys. Fluids 12, 245–248.Google Scholar
Vincent, A. & Meneguzzi, M. 1991 The spatial structure and statistical properties of homogeneous turbulence. J. Fluid Mech. 225, 1–20.Google Scholar
Waite, M. L. & Bartello, P. 2004 Stratified turbulence dominated by vortical motion. J. Fluid Mech. 517, 281–308.CrossRefGoogle Scholar
Waite, M. L. & Smolarkiewicz, P. 2007 Instability and breakdown of a vertical vortex pair in a strongly stratified fluid. J. Fluid Mech. (submitted).Google Scholar

Deloncle supplementary movies

Movie 1. Pseudo-spectral numerical simulation of the nonlinear evolution of a pair of counter-rotating vertical vortices in a stratified fluid for a Froude number F_h = 0.66 and a Reynolds number Re = 1060 (run labelled F0.6R1 in the paper). The vortices, initially straight along the vertical, are bent as a whole by the zigzag instability producing high vertical shear. Vertical vorticity isosurfaces are plotted: red and deep blue contours represent respectively plus and minus 60% of the vertical average of the maximum vertical vorticity in each horizontal plane. Transparent yellowish and bluish isosurfaces are the same, but for a 10% level.

Download Deloncle supplementary movies(Video)
Video 1.1 MB

Deloncle supplementary movies

Movie 2. Similar to Movie 1 but for the simulation F0.6R3 (F_h = 0.66, Re = 3180). The small-scale structures that appear correspond to Kelvin-Helmholtz instabilities.

Download Deloncle supplementary movies(Video)
Video 1.8 MB