Published online by Cambridge University Press: 21 May 2018
We study buoyancy-driven exchange flow of two mixtures in a vertical narrow duct (two-dimensional channel as well as pipe) theoretically. While the light mixture is assumed always to be a pure fluid, the heavy mixture can be selected as either a pure or a particle-laden fluid. A small width-to-length ratio considered for the duct (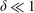 $\unicode[STIX]{x1D6FF}\ll 1$) has been used as the perturbation parameter in developing a lubrication model (negligible inertia). In particular, we have adopted the methodology of Zhou et al. (Phys. Rev. Lett., vol. 94, 2005, 117803) for free-surface particle-laden film flows and extended it to a lock exchange system in confined geometry under the Boussinesq approximation. The resulting model is in the form of the classical Riemann problem and has been solved numerically using a robust total variation diminishing finite difference scheme. Both pure and particle-laden cases are investigated in detail. It is observed that the interface between the two fluids takes a self-similar shape at long times. In the case that both heavy and light fluids are pure, the dynamics of the flow is governed by two dimensionless quantities, namely the Reynolds number,
$\unicode[STIX]{x1D6FF}\ll 1$) has been used as the perturbation parameter in developing a lubrication model (negligible inertia). In particular, we have adopted the methodology of Zhou et al. (Phys. Rev. Lett., vol. 94, 2005, 117803) for free-surface particle-laden film flows and extended it to a lock exchange system in confined geometry under the Boussinesq approximation. The resulting model is in the form of the classical Riemann problem and has been solved numerically using a robust total variation diminishing finite difference scheme. Both pure and particle-laden cases are investigated in detail. It is observed that the interface between the two fluids takes a self-similar shape at long times. In the case that both heavy and light fluids are pure, the dynamics of the flow is governed by two dimensionless quantities, namely the Reynolds number, 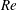 $Re$, and the viscosity ratio,
$Re$, and the viscosity ratio,  $\unicode[STIX]{x1D705}$, of the light and heavy fluids. The interpenetration of the heavy and light layers increases with
$\unicode[STIX]{x1D705}$, of the light and heavy fluids. The interpenetration of the heavy and light layers increases with 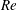 $Re$ but decreases with
$Re$ but decreases with  $\unicode[STIX]{x1D705}$. Also, the heights of the heavy and light fronts change with
$\unicode[STIX]{x1D705}$. Also, the heights of the heavy and light fronts change with  $\unicode[STIX]{x1D705}$ but remain unchanged with
$\unicode[STIX]{x1D705}$ but remain unchanged with 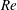 $Re$. In the case of the particle-laden flow, however, four additional dimensionless parameters emerge, namely the initial volume fraction of particles,
$Re$. In the case of the particle-laden flow, however, four additional dimensionless parameters emerge, namely the initial volume fraction of particles, 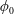 $\unicode[STIX]{x1D719}_{0}$, the ratio of particle diameter to duct width,
$\unicode[STIX]{x1D719}_{0}$, the ratio of particle diameter to duct width, 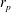 $r_{p}$, and the density ratios of particles to carrying fluid,
$r_{p}$, and the density ratios of particles to carrying fluid, 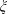 $\unicode[STIX]{x1D709}$, and of light fluid to carrying fluid,
$\unicode[STIX]{x1D709}$, and of light fluid to carrying fluid, 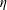 $\unicode[STIX]{x1D702}$. The effect of these parameters on the dynamics of the flow has been quantified through a systematic approach. In the presence of solid particles, the interface between the heavy and light layers becomes more curved compared to the case of pure fluids. This modification occurs due to the change of heavy mixture viscosity alongside the duct. Novel particle-rich zones are further discovered in the vicinity of the advancing heavy and light fronts. These zones are associated with different transport rates of the fluid and solid particles. The degree of particle enrichment remains the same with
$\unicode[STIX]{x1D702}$. The effect of these parameters on the dynamics of the flow has been quantified through a systematic approach. In the presence of solid particles, the interface between the heavy and light layers becomes more curved compared to the case of pure fluids. This modification occurs due to the change of heavy mixture viscosity alongside the duct. Novel particle-rich zones are further discovered in the vicinity of the advancing heavy and light fronts. These zones are associated with different transport rates of the fluid and solid particles. The degree of particle enrichment remains the same with 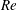 $Re$, is enhanced by
$Re$, is enhanced by  $\unicode[STIX]{x1D705}$,
$\unicode[STIX]{x1D705}$, 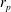 $r_{p}$ and
$r_{p}$ and 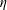 $\unicode[STIX]{x1D702}$, and is slightly diminished with
$\unicode[STIX]{x1D702}$, and is slightly diminished with 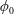 $\unicode[STIX]{x1D719}_{0}$ and
$\unicode[STIX]{x1D719}_{0}$ and 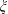 $\unicode[STIX]{x1D709}$. On the other hand, the stretched exchange zone between the heavy and light fronts grows with
$\unicode[STIX]{x1D709}$. On the other hand, the stretched exchange zone between the heavy and light fronts grows with 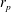 $r_{p}$,
$r_{p}$, 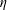 $\unicode[STIX]{x1D702}$ and
$\unicode[STIX]{x1D702}$ and 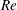 $Re$, but decays with
$Re$, but decays with 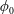 $\unicode[STIX]{x1D719}_{0}$,
$\unicode[STIX]{x1D719}_{0}$,  $\unicode[STIX]{x1D705}$ and
$\unicode[STIX]{x1D705}$ and 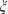 $\unicode[STIX]{x1D709}$.
$\unicode[STIX]{x1D709}$.