Mechanisms underlying how free surfaces influence very-large-scale motions in turbulent plane open channel flows based on linear non-modal analysis

Abstract

Linear non-modal analyses are performed to study the mechanism of how deformable free surfaces influence very-large-scale motions (VLSMs) in turbulent open channel flows. The mean velocity and eddy viscosity profiles obtained from direct numerical simulations are used in the generalised Orr–Sommerfeld and Squire equations to represent background turbulence effects. Solutions of surface-wave eigenmodes and shear eigenmodes are obtained. The results indicate that at high Froude numbers, free surfaces enhance the maximum transient growth rate of VLSMs through surface-wave eigenmodes. We then analyse the energy budget equation to reveal the underlying mechanism. For streamwise-uniform motions, the energy growth rate is enhanced by an energy production term associated with the correlation between the streamwise velocity, which is generated by the lifting-up effect of streamwise vortices composed of shear eigenmodes, and the vertical velocity, which is induced by a spanwise standing wave composed of surface-wave eigenmodes. For streamwise-varying motions, the energy growth rate is enhanced by a standing wave moving with a pair of vortices that travel at a speed approximately equal to the projection of the mean surface velocity along the wavenumber vector direction. Finally, an analytical expression of the energy production term is derived to provide the initial conditions for the maximum transient growth and explain the weak free-surface effect observed at large spanwise wavenumbers and low Froude numbers. The results demonstrate a linear non-modal mechanism in interactions between free surfaces and VLSMs in open channel flows.

1. Introduction

Flows in shallow open waters, such as continental shelves, rivers and channels, are characterised by turbulent shear flows with a free surface at the top. Research on turbulent flows in open channels is important for various applications, such as remote monitoring, environmental protection, aquaculture and river hydraulic engineering. Turbulent flows impinging on free surfaces can lead to surface deformation, which is a basis for non-invasive monitoring of underwater currents (Nichols et al. 2013; Legleiter, Mobley & Overstreet 2017). Moreover, the kinematic and dynamic boundary conditions of the free surface can constrain and distort turbulent motions, which control the transport of dissolved gases, pollutants and sediment in water (Hunt 1984; Jähne & Haußecker 1998). Research on the effects of free surfaces on turbulent motions in open channel flows aiming at elucidating the fundamental mechanisms underlying interactions between free surfaces and turbulence is crucial for providing a theoretical basis for developing turbulence models in various applications.

For turbulent flows under free surfaces, the Froude number $u^*/\sqrt {gl^*}$ is a key parameter that determines free surface deformation and turbulent flow properties, with $u^*$ being the characteristic velocity and $l^*$ being the characteristic length scale. It has been found that the effect of free surfaces can extend from the near-surface region to the bulk region as the Froude number increases. At low Froude numbers, the free surface mainly modulates turbulence eddies in the source layer near the surface (Rashidi & Banerjee 1988; Leighton et al. 1991; Handler et al. 1993; Komori, Nagaosa & Murikami 1993; Borue, Orszag & Staroselsky 1995; Shen et al. 1999), where the turbulence becomes anisotropic due to the constraint of the free surface vertical motions (Hunt & Graham 1978; Shen et al. 1999; Calmet & Magnaudet 2003). Yoshimura & Fujita (2020) performed direct numerical simulations and compared turbulence intensity in open channel flows at relatively high Froude numbers and in closed channel flows. They found that the intensity of streamwise velocity fluctuations in the outer layer increases slightly as the Froude number increases. Based on direct numerical simulations at low Reynolds numbers, Di et al. (2019) reported an increase in the energy spectrum of streamwise velocity fluctuations at low streamwise wavenumbers (with the corresponding length scale longer than six times the water depth) in the outer layer as the Froude number increases. Duan et al. (2020) conducted laboratory experiments at moderate Reynolds numbers and found that the streamwise velocity fluctuations in the outer layer, approximately one hundred wall units above the wall, are larger in open channel flows with a deformable free surface than in closed channel flows. This result was attributed to the amplification of the intensity of very-large-scale streamwise velocity fluctuations, which have a streamwise length scale approximately twenty times the water depth. These findings indicate that an increase in the Froude number can lead to an increase in the intensity of very-large-scale streamwise velocity fluctuations in the outer layer of open channel flows. The underlying mechanisms are the subject of our study.

The length scale of the turbulent motions enhanced by the presence of a free surface is consistent with that of very-large-scale motions (VLSMs) observed in the outer layer of wall-bounded turbulent flows. Specifically, in open channel flows, the streamwise length scale of VLSMs is typically of the order of ten times the water depth (Cameron, Nikora & Stewart 2017; Wang & Richter 2019; Duan et al. 2020; Peruzzi et al. 2020; Zampiron, Cameron & Nikora 2020; Pinelli et al. 2022), although it is influenced by the aspect ratio in open channel flows with sidewalls (Peruzzi et al. 2020; Zampiron et al. 2020). This length scale can be identified according to one of the distinct peaks in the bimodal distribution of the pre-multiplied streamwise energy spectrum of streamwise velocity fluctuations within the outer layer (Hutchins & Marusic 2007; Monty et al. 2007; Marusic, Mathis & Hutchins 2010). VLSMs are known to emerge under moderate to high Reynolds numbers (Hutchins & Marusic 2007), while the Reynolds numbers needed for generating VLSMs in open channels are much lower than those required in closed channels (Wang & Richter 2019; Duan et al. 2020; Peruzzi et al. 2020; Pinelli et al. 2022). For open channel flows with sidewalls, VLSMs are observed when the friction Reynolds number is greater than $614$ for a smooth bed (Duan et al. 2020) and greater than $442$ for a rough bed (Shen, Yang & Liu 2023). In recent direct numerical simulations of a plane open channel flow (without sidewalls) in a large computational domain, a weak peak located around $10h$ can also be observed in the pre-multiplied streamwise energy spectrum of the streamwise velocity fluctuations even when the friction Reynolds number is as low as $200$, and the spectral peak representing VLSMs becomes clear at the friction Reynolds number $365$ (Pinelli et al. 2022). Notably, in free-surface open channel flows, the amplification of turbulent motions with length scales comparable with those of VLSMs has been observed at relatively low and moderate Reynolds numbers. Hence, to discuss the effect of free surfaces on underwater turbulent motions (and vice versa), we broaden the scope of ‘VLSMs’ to include motions with length scales similar to those of VLSMs, removing the conventional restrictions of high Reynolds numbers in canonical wall-bounded turbulence.

VLSMs play an important role in momentum transfer in the outer layer of wall-bounded turbulent flows and have therefore attracted considerable attention (Kim & Adrian 1999; Guala, Hommema & Adrian 2006; Hutchins & Marusic 2007; Marusic et al. 2010). VLSMs manifest as low-speed streaks of streamwise velocity fluctuations and a hierarchy of hairpin vortex packets (Adrian & Marusic 2012). VLSMs contribute to more than $50\,\%$ of the streamwise velocity fluctuations and Reynolds shear stress in the outer layer of turbulent open channel flows at moderate Reynolds numbers (Duan et al. 2020), similar to observations in pipe flows and closed channel flows (Guala et al. 2006; Balakumar & Adrian 2007; Monty et al. 2007). Distinctly, VLSMs in free-surface open channel flows markedly influence the Reynolds shear stress near the free surface (Duan et al. 2020; Peruzzi et al. 2020), which differs from their counterparts in flat-plate boundary layers, closed channel flows and pipe flows (Guala et al. 2006; Hutchins & Marusic 2007; Monty et al. 2007). This notable intensity of VLSMs near the free surface can be linked to the impingement of hairpin vortices originating from the near-wall region on the surface (Nakagawa & Nezu 1977; Rashidi & Banerjee 1988; Gulliver & Halverson 1989; Nezu & Nakagawa 1997; Rashidi 1997; Tamburrino & Gulliver 2007), leading to surface signatures characterised by low-speed streak patterns (Lam & Banerjee 1992; Rashidi 1997; Tamburrino & Gulliver 2007; Cameron et al. 2017). Consequently, VLSMs can significantly impact surface renewal processes and scalar transport across free surfaces (Rashidi & Banerjee 1988; Komori, Murakami & Ueda 1989; Rashidi 1997; Pinelli et al. 2022).

Given the importance of VLSMs, as reviewed above, it is worth exploring the mechanism underlying the amplification of VLSMs with increasing Froude numbers in free-surface open channel flows. In this paper, we use the term ‘free-surface open channel’ to denote the case with a deformable free surface, as opposed to the ‘rigid-lid open channel’ case, in which the top boundary is a flat free-slip surface. We also note that it is widely recognised that interactions between externally generated waves and sheared currents in open channel flows lead to the formation of Langmuir-type cells exhibiting length scales comparable with those of VLSMs and intensities stronger than those of VLSMs in canonical wall-bounded turbulence (Gargett et al. 2004; Tejada-Martínez & Grosch 2007; Tejada-Martínez et al. 2013; Deng et al. 2019; Shrestha et al. 2019; Deng et al. 2020; Peruzzi et al. 2021). The Craik–Leibovich mechanism (Craik & Leibovich 1976; Leibovich 1977) attributes the development of Langmuir-type cells to the vortex force that results from the Stokes drift of water waves interacting with the vorticity. However, the waves occurring in free-surface open channel flows (Dolcetti et al. 2016; Yoshimura & Fujita 2020) are significantly weaker than the externally generated waves that lead to the generation of Langmuir-type cells (Gargett et al. 2004; Tejada-Martínez & Grosch 2007; Tejada-Martínez et al. 2013; Deng et al. 2019; Peruzzi et al. 2021); thus, the Craik–Leibovich mechanism is not suitable under these conditions. Consequently, further research is needed to investigate how the free surface enhances VLSMs in open channel flows.

In canonical wall-bounded turbulence, the generation of VLSMs is linked to a self-sustaining cycle involving VLSMs and large-scale motions (LSMs) (Cossu & Hwang 2017). This cycle encompasses three processes: the generation of streaks via the linear lift-up effect driven by streamwise vortices, the meandering of streaks through streak instability and/or transient growth, and the subsequent regeneration of streamwise vortices by nonlinear vortex stretching (Hwang & Bengana 2016). Cossu & Hwang (2017) confirmed that very-large-scale streaks can self-sustain by drawing energy directly from the mean flow using the linear non-modal analysis. Based on the very-large-scale streaks obtained by Cossu & Hwang (2017), de Giovanetti, Sung & Hwang (2017) further discovered that LSMs are generated by the linear instability of very-large-scale streaks in the outer region. In open channel flows, Camporeale et al. (2021) found that the linear instability induced by secondary currents occurs at the length scales of LSMs, suggesting that the generation mechanisms of LSMs in open channel flows are similar to those in canonical wall-bounded turbulence. However, few studies have been conducted on the free-surface effect on the linear lift-up process responsible for the generation of very-large-scale streaks.

The linear transient growth analysis has been found to be a useful tool for investigating the linear lift-up process responsible for the generation of streaks in wall-bounded turbulence (Butler & Farrell 1993; del Álamo & Jiménez 2006; Cossu, Pujals & Depardon 2009; Pujals et al. 2009; Hwang & Cossu 2010). Transient growth refers to the increase in the perturbation energy, even for stable flows, induced by the non-normality of the linearised Navier–Stokes operator (Trefethen et al. 1993; Schmid & Henningson 2001; Schmid 2007). del Álamo & Jiménez (2006) and Pujals et al. (2009) derived the generalised Orr–Sommerfeld and Squire equations based on the mean velocity and eddy viscosity profiles representing the effects of background turbulent fluctuations. Although the perturbation in the transient growth analysis is small, the linear lift-up effect responsible for the linear transient growth works well for perturbation in turbulence (Jimenez 2018). The generalised Orr–Sommerfeld and Squire equations have been used to study the response of turbulent flows to various boundary conditions (Cossu et al. 2009; Willis, Hwang & Cossu 2010; Deng et al. 2013; Song et al. 2015; Song, Huang & Xu 2017) and predict turbulence statistics in canonical wall-bounded turbulence (Illingworth, Monty & Marusic 2018). Regarding free-surface open channel flows, most of the previous linear stability analyses and non-modal analyses were performed based on the original Orr–Sommerfeld and Squire equations or the Rayleigh equation, and these works focused on the stability of streamwise-propagating surface waves in laminar base flows (Burns 1953; Yih 1972; Triantafyllou & Dimas 1989; Dimas & Triantafyllou 1994; Olsson & Henningson 1995; Ambrosi & Onorato 2008; Samanta 2020). Essentially, these studies investigated the transition from laminar flows to turbulent flows. To investigate the mechanism underlying how the free surface enhances VLSMs in fully developed turbulent open channel flows, there is a need to perform the non-modal transient growth analyses of turbulence in free-surface open channels based on the generalised Orr–Sommerfeld and Squire equations.

In this study, we perform a non-modal transient growth analysis based on the generalised Orr–Sommerfeld and Squire equations to study the transient growth in plane open channel flows with deformable free surfaces. We focus on the length scales where the transient growth rate is influenced by the free surface and study the underlying mechanisms, providing an explanation for the impact of free surfaces on underneath turbulent motions in open channel flows. The reminder of this paper is structured as follows. The mathematical formulation and computational method are introduced in § 2. In § 3, the transient growth rates are compared among cases with different Froude numbers to illustrate the effect of the free surface on turbulent motions. Then, the key mechanisms responsible for the increase in the transient growth rate due to the free surface are examined in § 4. Both streamwise-uniform and streamwise-varying motions are studied. The variation in the free-surface effect with the Froude number and wavenumber is also investigated at three different Reynolds numbers. Finally, the conclusions are given in § 5.

2. Mathematical formulation and computational method

We consider an incompressible viscous flow driven by a constant streamwise pressure gradient in a free-surface open channel. Because this study focuses on the free-surface effect, we employ plane open channel flows to exclude the influence of sidewalls on turbulent motions through secondary currents (Peruzzi et al. 2020; Zampiron et al. 2020). As depicted in figure 1, the plane open channel flow driven by a pressure gradient is periodic and statistically homogeneous in the streamwise and spanwise directions. This is a simplified model widely used in numerical studies to investigate free-surface effects (Komori et al. 1993; Borue et al. 1995; Pan & Banerjee 1995; Wang & Richter 2019; Pinelli et al. 2022). Following the rationales of previous linear non-modal analyses in canonical wall-bounded turbulence (Reynolds & Hussain 1972; Butler & Farrell 1992; del Álamo & Jiménez 2006; Pujals et al. 2009), the linear transient growth of the small-magnitude perturbations $\boldsymbol {u}=({u,v,w})$, $p$ and $\eta$ in a mean flow with $\boldsymbol {U}=(U(y), 0, 0)$ is studied to investigate the influence of the free surface. Here, $u$ (or $u_1$), $v$ (or $u_2$) and $w$ (or $u_3$) are the velocity perturbations in the streamwise ($x$ or $x_1$), vertical ($y$ or $x_2$) and spanwise ($z$ or $x_3$) directions, $p$ is the disturbed pressure, and $\eta$ is the surface height perturbation with respect to the mean surface height $y=h$.

Figure 1. Sketch of free-surface open channel flows without sidewalls. The flow is periodic and homogenous in the streamwise ($x$) and spanwise ($z$) directions.

2.1. Linearised equations and boundary conditions

The perturbations $\boldsymbol {u}$ and $p$ satisfy the continuity equation

(2.1)\begin{equation} \boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{u}=0 \end{equation}

and the linearised momentum equation (Pujals et al. 2009)

(2.2)\begin{equation} \frac{\partial \boldsymbol{u}}{\partial t} + U\frac{\partial{\boldsymbol{u}}}{\partial x} + \left( v U^\prime, 0 , 0 \right) ={-}\boldsymbol{\nabla} p + \boldsymbol{\nabla} \boldsymbol{\cdot} \left( \nu_T\left(\boldsymbol{\nabla} \boldsymbol{u} + \boldsymbol{\nabla} \boldsymbol{u}^{\rm T}\right)\right). \end{equation}

The total viscosity $\nu _T$ is equal to the sum of the molecular viscosity $\nu$ and the turbulent eddy viscosity $\nu _t$, which varies in the vertical direction. Hereinafter, the superscripts ‘$\prime$’ and ‘$\prime \prime$’ indicate the first- and second-order derivatives in the vertical direction, respectively. The superscript ‘$T$’ represents the transpose of vectors and matrices.

Because the free surface is a material surface, $\eta$ satisfies the kinematic boundary condition (Mei, Stiassnie & Yue 2005)

(2.3)\begin{equation} \frac{\partial \eta}{\partial t} + (U+u)\frac{\partial \eta}{\partial x} + w \frac{\partial \eta}{\partial z} = v,\quad \mathrm{at}\ y=h + \eta. \end{equation}

In the present study, the pressure and shear stress imposed at the surface by the air are zero, and the surface tension is negligible, as we focus on VLSMs. Therefore, the perturbations satisfy the following free-surface dynamic boundary conditions:

(2.4)\begin{equation} \boldsymbol{n} \boldsymbol{\cdot} \boldsymbol{\sigma} \boldsymbol{\cdot} \boldsymbol{n} = 0,\quad \boldsymbol{t_1}\boldsymbol{\cdot} \boldsymbol{\sigma} \boldsymbol{\cdot} \boldsymbol{n} =0,\quad \boldsymbol{t_2}\boldsymbol{\cdot} \boldsymbol{\sigma} \boldsymbol{\cdot} \boldsymbol{n} = 0,\quad \mathrm{at}\ y=h + \eta. \end{equation}

In (2.4), the first equation represents the equilibrium of the normal stress, and the second and third equations respectively represent the balance of the shear stresses in the tangential directions $\boldsymbol {t_1}$ and $\boldsymbol {t_2}$. The stress tensor $\boldsymbol {\sigma }$ is defined as $(-p-P+gy)\boldsymbol {I} + \nu (\boldsymbol {\nabla } (\boldsymbol {U}+\boldsymbol {u}) + \boldsymbol {\nabla } (\boldsymbol {U}^{\rm T}+\boldsymbol {u}^{\rm T}))$, where $\boldsymbol {I}$ is the identity matrix, $P$ is the mean pressure and $g$ is the gravitational acceleration. The unit vectors $\boldsymbol {n}$, $\boldsymbol {t_1}$ and $\boldsymbol {t_2}$ are expressed as

(2.5a–c)\begin{align} {\boldsymbol{n}=\frac{(-\partial\eta/\partial x, 1, -\partial\eta/\partial z)}{\sqrt{(\partial\eta/\partial x)^2+1+(\partial\eta/\partial z)^2}},\quad \boldsymbol{t_1}=\frac{(1, \partial\eta/\partial x, 0)}{\sqrt{(\partial\eta/\partial x)^2+1}},\quad \boldsymbol{t_2}=\frac{(0, \partial\eta/\partial z, 1)}{\sqrt{(\partial\eta/\partial z)^2+1}}}. \end{align}

Substituting the Taylor series of the perturbations $\boldsymbol {u}$ and $p$ at $y=h$ into (2.3)–(2.4) and retaining the first-order terms of $\eta$, the free-surface boundary conditions (2.3)–(2.4) are linearised as

(2.6)$$\begin{gather} \frac{\partial \eta}{\partial t} + U\frac{\partial \eta}{\partial x} = v, \end{gather}$$

(2.7)$$\begin{gather}-p+g\eta = 2\nu \left(U^\prime\eta_x - \frac{\partial v}{\partial y}\right), \end{gather}$$

(2.8)$$\begin{gather}\frac{\partial u}{\partial y}+\frac{\partial v} {\partial x} ={-}U^{\prime\prime}\eta, \end{gather}$$

(2.9)$$\begin{gather}\frac{\partial w}{\partial y}+\frac{\partial v} {\partial z} = 0, \end{gather}$$

at $y=h$. The bottom is a no-slip wall, i.e. $\boldsymbol {u} = 0$ at $y=0$.

By eliminating the pressure term in (2.2) using the continuity equation (2.1), the generalised Orr–Sommerfeld and Squire equations for the vertical velocity $v$ and vertical vorticity $\omega _y$ can be obtained (Schmid & Henningson 2001). We assume that the perturbations in turbulent open channel flows have wave-like forms, i.e.

(2.10)\begin{equation} (v, \omega_y, \eta) = \left(\hat{v}(y),\hat{\omega}_y(y),\hat{\eta}\right)\exp({{\rm i}(\alpha x +\beta z-\lambda t)})+{\rm c.c.}, \end{equation}

where ${\rm c.c.}$ is the complex conjugation. The generalised Orr–Sommerfeld and Squire equations in the spectral space can be written as

(2.11)$$\begin{gather} -{\rm i}\lambda (\mathrm{D}^2-k^2) \hat{v} = L_{OS} \hat{v}, \end{gather}$$

(2.12)$$\begin{gather}-{\rm i}\lambda \hat{\omega}_y ={-}{\rm i}\beta U^\prime \hat{v} + L_{SQ} \hat{\omega}_y. \end{gather}$$

Hereinafter, $\lambda$ is a complex eigenvalue and $k^2= \alpha ^2+\beta ^2$, where $\alpha$ and $\beta$ are the wavenumbers in the streamwise and spanwise directions, respectively. The notation $\mathrm {D}$ denotes the vertical derivative of the perturbations. The coupling term $-{\rm i}\beta U^\prime \hat {v}$ is an important source of the non-orthogonality of the linearised equations. This coupling term leads to the generation of the elongated streaks in the streamwise direction, represented by the vertical vorticity in wall-bounded turbulence, through the interaction between the shear of the base flow and the spanwise-varying vertical velocity, which is known as the ‘lifting-up’ effect (Ellingsen & Plam 1975). The operators $L_{OS}$ and $L_{SQ}$ are expressed as (Pujals et al. 2009)

(2.13) $$\begin{gather} L_{OS} ={-}{\rm i} \alpha [U(\mathrm{D}^2-k^2)-U^{\prime\prime}] + \nu_T (\mathrm{D}^2-k^2)^2 + 2 \nu_T^\prime (\mathrm{D}^3-k^2\mathrm{D}) + \nu_T^{\prime \prime} (\mathrm{D}^2+k^2), \end{gather}$$

(2.14) $$\begin{gather}L_{SQ} ={-}{\rm i} \alpha U + \nu_T(\mathrm{D}^2-k^2) + \nu_T^\prime \mathrm{D}. \end{gather}$$

The linearised free-surface boundary conditions at $y=h$ in (2.6)–(2.9) can be rewritten as

(2.15)$$\begin{gather} -{\rm i}\lambda\hat{\eta} + {\rm i}\alpha U \hat{\eta} = \hat{v}, \end{gather}$$

(2.16) $$\begin{gather}{[}-{\rm i}\lambda + {\rm i}\alpha U - \nu_T(\mathrm{D}^2-k^2)+ 2\nu k^2] \mathrm{D}{\hat{v}} =[{\rm i}\alpha U^\prime+\nu_T^\prime(\mathrm{D}^2+k^2)]\hat{v} + ({-}g + 2{\rm i}\nu \alpha U^\prime)k^2\hat{\eta}, \end{gather}$$

(2.17)$$\begin{gather}-(\mathrm{D}^2+k^2)\hat{v}={-} {\rm i} \alpha \hat{\eta} U^{\prime\prime}, \end{gather}$$

(2.18)$$\begin{gather}\mathrm{D}\hat{\omega}_y = {\rm i}\beta \hat{\eta} U^{\prime\prime}. \end{gather}$$

The above linearised free-surface boundary conditions can regress to the rigid free-slip lid conditions ($\eta =0$) for infinitely small Froude numbers $Fr_\tau \rightarrow 0$. In the present study, the friction Froude number $Fr_\tau$ is defined based on the friction velocity $u_\tau$ at the bottom wall, $h$ and $g$ as $Fr_\tau =u_\tau /\sqrt {gh}$. The no-slip boundary conditions expressed by $\hat {v}$ and $\hat {\omega }_y$ at $y=0$ are

(2.19)\begin{equation} \hat{v} = \hat{\omega}_y = 0. \end{equation}

Compared with the linear transient growth analysis of laminar flows in free-surface open channels conducted by Olsson & Henningson (1995), we consider turbulence effects, including the mean velocity of the turbulent flow and the eddy viscosity induced by background turbulence. Because the mean velocity is relatively insensitive to the Froude number (Yoshimura & Fujita 2020), the mean velocity profile $U(y)$ in an open channel with a rigid-lid surface is selected as the base flow. We mainly consider four friction Reynolds numbers $Re_\tau =180$, $360$, $1000$ and $6000$. The friction Reynolds number is defined as $Re_\tau =u_\tau h/\nu$, where $u_\tau$ is the friction velocity at the bottom wall. The mean velocity and total viscosity profiles at $Re_\tau =180$, $360$ and $1000$ are obtained using direct numerical simulations based on a spectral and finite-differential method (Kermani et al. 2011). The mean velocity and the eddy viscosity at $Re_\tau =6000$ are obtained using the data from Pirozzoli (2023). The profiles of the mean velocity $U$ and total viscosity $\nu _T$ are depicted in figure 2. The non-zero $\nu _T$ at the free surface is calculated using L’Hôpital's rule (Shen, Triantafyllou & Yue 2000). The distributions of $U$ and $\nu _T$ are similar to those shown by Borue et al. (1995). The surface mean velocity and bulk total eddy viscosity increase with increasing Reynolds number. However, $\nu _T$ in the outer layer of open channel flows is much smaller than what is determined by the Cess expression in closed channel flows (Pujals et al. 2009). Therefore, similar to the linear non-modal analysis in turbulent Couette flow conducted by Hwang & Cossu (2010), we use the $U$ and $\nu _T$ profiles obtained from the direct numerical simulations, instead of the Cess expression, in our transient analyses below.

Figure 2. Profiles of the mean velocity $U$ and the total viscosity $\nu _T$ at $Re_\tau =180$, $360$, $1000$ and $6000$.

In our studies, we mainly consider four friction Froude numbers $Fr_\tau = 0$, $0.05$, $0.1$ and $0.142$. The corresponding bulk Froude numbers $Fr_b$, defined based on the bulk mean velocity $U_m$ as $Fr_b = U_m / \sqrt {gh}$, at different Reynolds numbers are listed in table 1. According to Brocchini & Peregrine (2001), wave breaking in open shallow waters primarily occurs when the turbulent Froude number, defined as $F_{BP} = q / \sqrt {2gL}$, exceeds $0.225$. In their work, $q$ represents the turbulent intensity near the water surface, and $L$ is the length scale of the most energetic turbulent motion near the surface. The two Froude numbers $Fr_\tau$ and $F_{BP}$ satisfy the relation $Fr_\tau = F_{BP} \sqrt {2L/h} (u_\tau / q)$. In open channel flows, the turbulent intensity $q$ is close to $u_\tau$, and $L \approx 1\unicode{x2013}10h$ (Pirozzoli 2023), leading to $Fr_\tau = 1.412F_{BP}\unicode{x2013}4.47F_{BP}$. Consequently, surface breaking typically occurs for $Fr_\tau > 0.312$. It has also been observed in laboratory experiments (Auel, Albayrak & Boes 2014) that no air entrainment or wave breaking occurred even for the bulk Froude number $Fr_b = 3.5$. Thus, for plane open channel flows, the Froude numbers used in the present study (table 1) are below the threshold for breaking free surfaces.

Table 1. Friction Froude number $Fr_\tau$ and the corresponding bulk Froude number $Fr_b$ at Reynolds numbers $Re_\tau =180$, $360$, $1000$ and $6000$ considered in the present study.

2.2. Computation method for the transient growth rate

The energy growth rate for the non-dimensional wavenumber $(\alpha h,\beta h)$ is defined as

(2.20)\begin{equation} G(\alpha h, \beta h, t) = \sup_{E^{in}\neq 0}\frac{E(\alpha h, \beta h, t)}{E^{in}}. \end{equation}

Here, $E$ is the total energy, which is defined as

(2.21)\begin{align} E(\alpha h, \beta h, t) =\underbrace{\frac{1}{2k^2} \int_0^h \left ({\rm D}\hat{v} ({\rm D}{\hat{v}})^{*} + k^2 \hat{v} \hat{v}^{*}+ \hat{\omega}_y (\hat{\omega}_y)^* \right)\,{\rm d} y}_{E_K}+\underbrace{\frac{1}{2}g\hat{\eta} \hat{\eta}^*}_{E_\eta}=\boldsymbol{q}^*\boldsymbol{M}\boldsymbol{q}. \end{align}

In the above equation, $E_{K}$ is the kinetic energy and $E_\eta$ is the potential energy. For the vector $\boldsymbol {q}=({\hat {v}},\hat {\omega }_y,\hat {\eta })^{\rm T}$, the superscript ‘$*$’ indicates the conjugated transpose of a vector or a matrix. The energy matrix $\boldsymbol {M}$ is an operator to compute the energy of the vector $\boldsymbol {q}$. As analysed below in § 4, energy is transformed between $E_{K}$ and $E_\eta$. Therefore, only the growth rate of the total energy $E$ is meaningful from the viewpoint of energy conservation. The superscript ‘$in$’ refers to the initial energy at $t=0$. The symbol ‘$sup$’ indicates the supremum.

The total energy can be expressed by the eigenmodes $\bar {\boldsymbol {q}}$ and eigenvalues $\lambda$ of the linearised system (2.11)–(2.19). Assume an expansion of $\boldsymbol {q}$ using the eigenmodes, $\boldsymbol {q} (t)=\boldsymbol {S}\boldsymbol {\kappa }(t)$, in which the columns of matrix $\boldsymbol {S}$ are the eigenmode $\bar {\boldsymbol {q}}$. The parameter vector $\boldsymbol {\kappa }(t)$ satisfies

(2.22)\begin{equation} \boldsymbol{\kappa}(t)=\exp\left(-{\rm i}\varLambda t\right)\boldsymbol{\kappa}(t=0), \end{equation}

in which the diagonal elements of the diagonal matrix $\varLambda$ are the eigenvalues $\lambda$. Therefore,

(2.23)\begin{equation} \boldsymbol{q}(t) =\boldsymbol{S}\exp\left(-{\rm i}\varLambda t\right) \boldsymbol{\kappa}(t=0). \end{equation}

Decompose the Hermitian energy matrix $\boldsymbol {M}$ into $\boldsymbol {M}=\boldsymbol {F}^*\boldsymbol {F}$, and then the total energy in (2.21) can be further written as

(2.24)\begin{equation} {E(\alpha h, \beta h, t) =\lVert \boldsymbol{F}\boldsymbol{S}\exp\left(-{\rm i}\varLambda t\right) \boldsymbol\kappa(t=0)\rVert_2^2}. \end{equation}

Here, $\lVert \rVert _2$ represents the 2-norm of the matrix. Then, the energy growth rate can be expressed as (Schmid & Henningson 2001)

(2.25)\begin{equation} {G(\alpha h, \beta h, t) = \sup_{E^{in}\neq 0}\lVert\boldsymbol{F} \boldsymbol{S}\exp\left(-{\rm i}\varLambda t\right)\boldsymbol{S}^{{-}1}\boldsymbol{F}^{{-}1}\rVert_2^2=\lVert\boldsymbol{A}\rVert_2^2. } \end{equation}

The value of $G(\alpha h, \beta h, t)$ and the corresponding initial and amplified perturbations are solved by the singular value decomposition of the matrix $\boldsymbol {\varTheta }^*\boldsymbol {A}\boldsymbol {\varUpsilon }= \boldsymbol {\varXi }$. The elements of the diagonal matrix $\boldsymbol {\varXi }$ are the singular values of $\boldsymbol {A}$. Here, $G(\alpha h, \beta h, t)$ is equal to the largest singular value, and the initial and amplified perturbations are the corresponding columns of the unitary matrices $\boldsymbol {\varTheta }$ and $\boldsymbol {\varUpsilon }$, respectively.

The eigenmodes $\bar {\boldsymbol {q}}$ and eigenvalues $\lambda$ of the linearised system (2.11)–(2.19) are solved using a Chebyshev spectral collocation method on a grid of $N_y+1$ collocation points. The real part of the eigenvalue, $\lambda _r$, represents the frequency of the perturbation, and $\lambda _r/k$ represents the advection velocity of the perturbation along the direction of $(\alpha h, \beta h)$. The imaginary part $\lambda _i$ indicates the temporal stability of the system. The system is unstable if $\lambda _i$ is positive. In the present study, $N_y=96$, $128$, $192$ and $384$ are used for $Re_\tau =180$, $360$, $1000$ and $6000$, respectively. The convergence of the results has been validated by doubling $N_y$. The code has been validated in our previous study in closed channel flows (Deng et al. 2013).

The maximum transient growth rate for the non-dimensional wavenumber $(\alpha h, \beta h)$ is

(2.26)\begin{equation} G_{max}(\alpha h, \beta h) = \max_{t}G(\alpha h, \beta h,t)= G(\alpha h, \beta h,t_{max}), \end{equation}

where $t_{max}$ represents the instant at which the maximum transient growth rate is obtained. In the non-modal analyses of canonical wall-bounded turbulence (del Álamo & Jiménez 2006; Cossu et al. 2009; Pujals et al. 2009; Willis et al. 2010; Song et al. 2015, 2017), the amplified perturbations corresponding to $G_{max}$ have been shown to include the most energetic turbulent motions to a certain extent, and the initial perturbations can provide the conditions for generating these turbulent motions. Moreover, the variance in $G_{max}$ serves as an indicator to assess the difference in the intensities among these turbulent motions.

3. Impact of the free surface on linear transient growth and stability

In this section, the effect of the free surface is first studied by comparing the transient growth rate at different Froude numbers, and then the influence of the free surface on the stability is discussed.

3.1. Transient growth rate in free-surface open channel flows

Figure 3 compares the contours of the maximum transient growth rate $G_{max}(\alpha h, \beta h)$ at $Fr_\tau =0.05$, $0.1$ and $0.142$ with that at $Fr_\tau =0$ (rigid free-slip lid case) for $Re_\tau =180$. The transient growth mainly occurs in the region of $\alpha h<\beta h$. For any given spanwise wavenumber $\beta h$, $G_{max}$ increases as the streamwise wavenumber $\alpha h$ decreases, reaching its maximum value at $\alpha h = 0$. These two features are similar to those observed in closed channel flows (del Álamo & Jiménez 2006; Cossu et al. 2009). Figure 4 further compares $G_{max}$ in different cases and the relative increase rate of $G_{max}$ in the cases with deformable free surface with respect to that in the rigid-lid case for $\alpha h=0$. As shown in figure 4(a), the peaks of $G_{max}$ at different Froude numbers all occur at approximately $(\alpha h, \beta h)=(0, 2.7)$. The value of $G_{max}$ is insensitive to the free surface when $\beta h>2.7$. However, as the Froude number increases from $Fr_\tau =0.05$ to $Fr_\tau =0.142$, $G_{max}$ increases with $Fr_\tau$ when $\beta h<2.7$, and this growth is more obvious with lower $\beta h$ (figure 4b).

Figure 3. Comparison of the contours of the maximum transient growth rate $G_{max}(\alpha h, \beta h)$ at (a) $Fr_\tau =0.05$, (b) $Fr_\tau =0.1$ and (c) $Fr_\tau =0.142$ with those at $Fr_\tau = 0$ for $Re_\tau =180$. The white dashed lines represent $\alpha h = \beta h$. The solid black contours are $G_{max}$ in the rigid-lid case ($Fr_\tau =0$), with its value changing from 1.4 to 5 with an interval 0.4 (the same as the colour contours).

Figure 4. Comparison of (a) the maximum transient growth rate $G_{max}$ at $Fr_\tau =0$ (rigid-lid case), $0.05$, $0.1$ and $0.142$ and (b) the relative increase rate, $R_{Gmax}$, of $G_{max}$ in the deformable free surface cases ($Fr_\tau =0.05$, $0.1$ and $0.142$) with respect to that in the rigid-lid case ($Fr_\tau =0$). The results shown are for $\alpha h =0$ at $Re_\tau =180$.

To investigate the relationship between the free-surface effect on the transient growth and the influence of the free surface on turbulent motions that has been observed in experiments (Duan et al. 2020) and direct numerical simulations (Di et al. 2019), we analyse the effect of the free surface on the growth rate of the kinetic energy $G_{K}$ corresponding to $G_{max}$. Here, $G_{K}$ is defined based on the optimal input and output perturbations corresponding to $G_{max}$ as

(3.1)\begin{equation} G_{K}(\alpha h, \beta h, t_{max})=\frac{E_{K}^{out}(\alpha h, \beta h)}{E_{K}^{in}(\alpha h, \beta h)}=\frac{R_{K}^{out} E^{out}(\alpha h, \beta h)}{R_{K}^{in}E^{in}(\alpha h, \beta h)}=\frac{R_{K}^{out}}{R_{K}^{in}}G_{max}(\alpha h, \beta h), \end{equation}

where $R_{K}$ is the ratio of the kinetic energy to the total energy. If the ratio is larger for the amplified output perturbation than for the input perturbation, i.e. $R_{K}^{in}< R_{K}^{out}\leq 1$, $G_{K}>G_{max}>G_{\eta }$, indicating that potential energy is transformed into kinetic energy during the transient growth process. Here, $G_{\eta }$ is the growth rate of the potential energy, which is defined as

(3.2)\begin{equation} G_{\eta}(\alpha h, \beta h, t_{max})=\frac{E_{\eta}^{out}(\alpha h, \beta h)}{E_{\eta}^{in}(\alpha h, \beta h)}=\frac{R_{\eta}^{out}}{R_{\eta}^{in}}G_{max}(\alpha h, \beta h), \end{equation}

where $R_{\eta }$ is the ratio of the potential energy to the total energy. If $R_{K}^{out}< R_{K}^{in}\leq 1$, kinetic energy is transformed into potential energy during the transient growth process, leading to $G_{\eta }>G_{max}>G_{K}$.

Figure 5 shows a comparison of $G_{max}$, $G_{K}$ and $G_{K}/G_{max}$ at different Froude numbers and $Re_\tau =180$. At $Fr_\tau =0$, the distribution of $G_{K}$ is the same as that of $G_{max}$ due to the zero $\eta$. As the Froude number increases, $G_{K}$ differs from $G_{max}$. For $\alpha h < \beta h<2.7$, where $G_{max}$ is enhanced by the free surface, $G_{K}/G_{max}$ is close to or even larger than $1$. Especially, $G_{K}/G_{max}$ is obviously larger than 1 when $\alpha h < \beta h<1$, with its largest value located at $\alpha h=0$ (figure 5c iii). Therefore, when $\alpha h < \beta h<2.7$, the growth rate of the kinetic energy also increases with increasing Froude number, with $G_K$ being obviously greater than $G_{max}$ for $\alpha h < \beta h<1$.

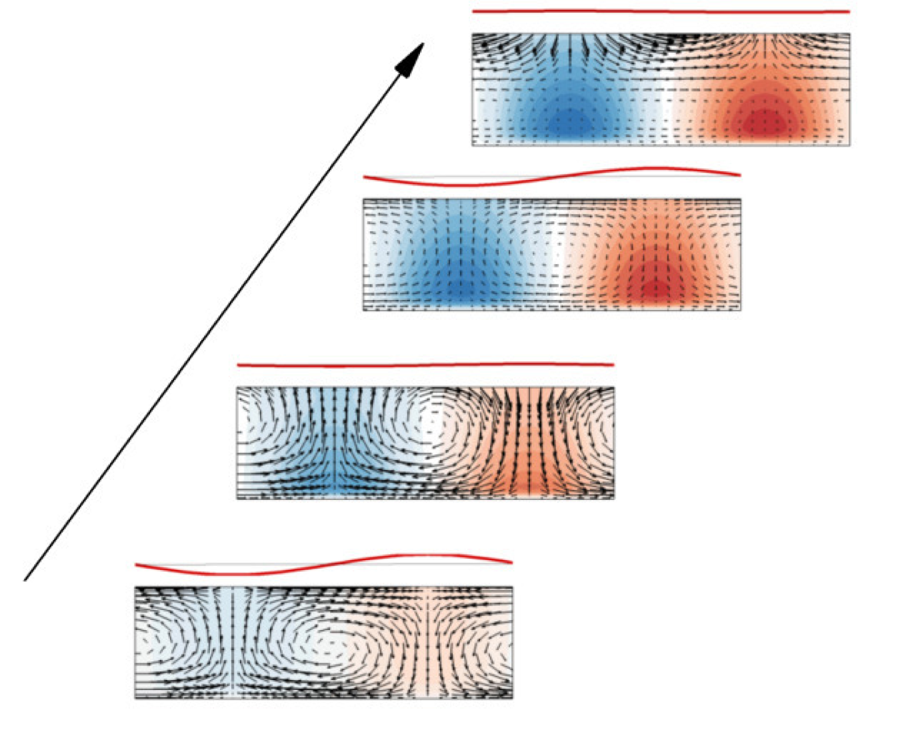
Figure 5. Comparison of (a i–iii) the maximum transient growth rate $G_{max}(\alpha h, \beta h)$, (b i–iii) the corresponding growth rate of the kinetic energy $G_{K}(\alpha h, \beta h)$ and (c i–iii) the ratio $G_{K}(\alpha h, \beta h)/G_{max}(\alpha h, \beta h)$ at Froude numbers $Fr_\tau =$ (a i,b i,c i) 0.05, (a ii,b ii,c ii) $0.1$ and (a iii,b iii,c iii) $0.142$ with the rigid-lid case ($Fr_\tau =0$) at $Re_\tau =180$. The black solid contour lines are the results in the rigid-lid case, with its value changing from 1.4 to 5 with an interval 0.4 (the same as the colour contours). The black dashed contour lines represent the locations where the imaginary part of the eigenvalue $\lambda _i=0$. The white dashed lines represent $\alpha h = \beta h$.

The effect of the free surface on $G_K$ found at $Re_\tau = 180$ also exists at $Re_\tau = 360$, $1000$ and $6000$. Figure 6 compares $G_K$ at different Froude numbers for $\alpha h = 0$ when $Re_\tau = 180$, $360$, $1000$ and $6000$. There are two peaks in $G_K$ at different Reynolds numbers. The wavenumber of one peak is well scaled by the viscous length at approximately $\beta \nu / u_\tau = 0.07$, corresponding to the spanwise spacing of near-wall streaks. The other peak lies at approximately $\beta h = 2.4$, which agrees with the spanwise length scale of VLSMs $\lambda _z / h = 1-3$ in plane open channel flows (Wang & Richter 2019; Pinelli et al. 2022). It should be noted that these two peaks of $G_K$ at $Re_\tau = 180$ are close to each other with comparable values, and the two peaks are more widely separated as the Reynolds number increases from $Re_\tau = 360$ to $6000$. While VLSMs were not observed at Reynolds numbers lower than $442$ in the experiments of open channel flows with sidewalls (Shen et al. 2023), recent direct numerical simulations of plane open channel flows (Pinelli et al. 2022) showed that the bimodal distribution of the pre-multiplied streamwise energy spectrum of the streamwise velocity fluctuations in the outer layer is clear at $Re_\tau \geq 365$, and the peak at the length scale of VLSMs becomes weaker at a lower Reynolds number $Re_\tau = 200$. As such, the variation of the peak located around $\lambda _z / h = 2.4$ with the Reynolds number in figure 6 is similar to VLSMs in plane open channel flows.

Figure 6. Influence of the Froude number on the growth rate of the kinetic energy $G_{K}(\alpha h, \beta h)$ corresponding to $G_{max}$ for $\alpha h=0$ at (a) $Re_\tau =180$, (b) $360$, (c) $1000$ and (d) $6000$. The first peaks are located at approximately $\beta h=2.4$ (corresponding to $\lambda _z/h=2.6$), and the secondary peaks are located at approximately $\beta \nu /u_\tau =0.07$ (corresponding to $\lambda _z^+=90$).

As shown in figure 6, at these four Reynolds numbers, $G_K$ grows with the Froude number for $\beta h \leq 2.4$, and the enhancement is more pronounced as $\beta h$ decreases. From figure 7, it can be further confirmed that the enhancement of $G_K$ by the free surface occurs for $\alpha h < \beta h$, i.e. the streamwise-elongated motions, at $Re_\tau = 360$, $1000$ and $6000$. Although the value of $G_{K}$ ($G_{max}$ for the rigid-lid case) around the peak located at approximately $\beta h =2.4$ also slightly increases with the Reynolds number, similar to the finding that the intensity of VLSMs grows with the Reynolds number (Marusic et al. 2010; Pinelli et al. 2022; Pirozzoli 2023), the Froude number effect is distinct at even smaller wavenumbers. For a specified Reynolds number, the effect of free surfaces deserves attention. The above analysis suggests that the free-surface effect on the transient growth rate is consistent at least for $180 \leq Re_\tau \leq 6000$ studied in this work, and the length scale range where the free-surface effect is felt aligns with the length scale of the streamwise-elongated VLSMs that are intensified at relatively high Froude numbers in free-surface open channel flows (Di et al. 2019; Duan et al. 2020).

Figure 7. Comparison of the growth rate of the kinetic energy $G_{K}(\alpha h, \beta h)$ corresponding to the maximum transient growth rate $G_{max}(\alpha h, \beta h)$ among different Froude numbers and Reynolds numbers. Panels (a i,b i,c i) and (a ii,b ii,c ii) show the results for $Fr_\tau =0.1$ and $0.142$, respectively, while panels (a i,ii), (b i,ii) and (c i,ii) show the results for $Re_\tau =360$, $1000$ and $6000$, respectively. Here, the black solid contour lines are the results at $Fr_\tau =0$, with its value changing from 1.5 to 6.5 with an interval of 0.5 (the same as the colour contours). The black dashed contour lines denote the locations for which the imaginary part of the eigenvalue is zero. The white dashed lines represent $\alpha h = \beta h$.

It should also be noted that the spanwise length scale of the peak, well scaled by $h$, in open channel flows is different from that in closed channel flows (Pujals et al. 2009). This discrepancy can be attributed to the differences in the symmetry of the mean flow and the boundary conditions. In closed channel flows, the mean velocity and boundary conditions are symmetric with respect to the channel centreline $y = h$, and hence there are two types of perturbations: one with symmetric vertical velocity and the other with asymmetric vertical velocity (Jimenez 2018). The perturbation leading to the peak in closed channel flows is a pair of streamwise vortices occupying the entire channel with symmetric vertical velocity (Pujals et al. 2009). However, due to the constraint imposed by the free surface, only the perturbation with asymmetric vertical velocity exists in rigid-lid open channel flows.

3.2. Unstable eigenmodes induced by the free surface

In addition to the influence of free surfaces on the transient growth of streamwise-elongated motions, as shown in figures 5(a ii,a iii) and 7, the free surface also induces unstable eigenmodes for spanwise-elongated motions ($\alpha h>\beta h$). In this section, we discuss these unstable eignmodes.

Figure 8(a,c) compares the eigenvalues in the free-surface open channel at $Fr_\tau = 0.142$ with those in the rigid-lid case at $Re_\tau = 180$ and $6000$, with $\alpha h = 0.4$ and $\beta h = 0$. There are two additional eigenvalues in the free-surface open channel case compared with the rigid-lid case. These two additional eigenvalues and the corresponding eigenmodes, induced by the free surface, are referred to as the ‘surface-wave eigenvalues’ and ‘surface-wave eigenmodes’, respectively, while the other eigenvalues and eigenmodes are called the ‘shear eigenvalues’ and ‘shear eigenmodes’, respectively (Yih 1972). In figure 8(b,d), the modulus of the vertical velocity $|\bar {v}|$ increases monotonically with $y/h$, reaching its maximum value at the surface and inducing surface deformation, which is another distinct feature of surface-wave eigenmodes compared with shear eigenmodes (Yih 1972).

Figure 8. (a,c) Comparison of eigenvalues $\lambda$ between the free-surface open channel with $Fr_\tau =0.142$ and the rigid-lid open channel. The points represent the eigenvalues of the shear eigenmodes in the free-surface open channel, the diamonds represent the eigenvalues of the surface-wave eigenmodes in the free-surface open channel and the hollow circles represent the eigenvalues in the rigid-lid open channel. (b,d) Vertical profiles of the velocity moduli of the surface-wave eigenmodes. The lines without symbols denote the results of the unstable surface-wave eigenmode and those with symbols denote the stable surface-wave eigenmode. The results are obtained at (a,b) $Re_\tau =180$ and (c,d) $6000$ for $\alpha h =0.4$ and $\beta h=0$.

As shown in figure 8(a,c), the propagation speeds $c = \lambda _r / \alpha$ of these two surface-wave eigenmodes are different. Assume that these two speeds are $c_1 = c_s + c_w$ and $c_2 = c_s - c_w$. It can be found that the values of $c_s$ (equal to $\lambda _r^s / \alpha$) at $Re_\tau = 180$ and $6000$ are approximately $16.3 u_\tau$ and $25u_\tau$, respectively, close to the mean velocity near the surface. The value of $c_w / u_\tau$ is close to the phase speed determined by the dispersion relationship $\sqrt {\tanh {(kh)}} / (Fr_\tau \sqrt {kh})$. The unstable eigenmode is the surface-wave eigenmode with $c_1 = c_s + c_w$.

In the stability analysis using the laminar base flow, the unstable surface-wave eigenmode also has been found at small $\alpha h$. For the horizontal plane open channel flow, the condition leading to the unstable eigenmodes is $Fr_b > 0.8$ (Olsson & Henningson 1995). In the present work, the unstable eigenmodes exist in supercritical cases. Because the mean velocity profile used in this study is complex, it is difficult to provide an exact formulation to determine the lowest unstable Froude numbers. We provide another feature based on the boundary condition. From (2.15), it can be derived that

(3.3)\begin{equation} {\hat{\eta} = \frac{\hat{v}}{-{\rm i}\lambda_r + {\rm i}\alpha U_s + \lambda_i} = \frac{\hat{v}}{|{\rm i}(\alpha U_s - \lambda_r) + \lambda_i|} \exp({\rm i}\theta), \quad \text{with} \ \tan\theta = \frac{\lambda_r - \alpha U_s}{\lambda_i}.} \end{equation}

Here, $U_s$ is the mean velocity at the free surface. For the free-surface eigenmode with $c_1 = c_s + c_w$, the flow is neutrally stable ($\lambda _i = 0$) when $\theta = -90^\circ$, and becomes unstable when $\theta > -90^\circ$. This is confirmed by figure 9, which shows that the range of $\beta h$ where $\theta + 90^\circ > 0$ (figure 9a,c) agrees with that with $\lambda _i>0$ (figure 9b,d) for different Reynolds numbers and Froude numbers. From figure 9, the streamwise length of these unstable eigenmodes is longer than $2{\rm \pi} h$, i.e. $\alpha h < 1$. These unstable modes are much longer than those obtained in the secondary stability analysis of open channel flows with secondary currents (close to $3h$) (Camporeale et al. 2021).

Figure 9. Variations of the phase difference between the vertical velocity and the surface elevation $\theta$ and the corresponding eigenvalue $\lambda _i$ with $\alpha h$ at $\beta h=0$ for the surface-wave eigenmodes with $c_1 = c_s + c_w$. (a) $\theta +90^\circ$ at $Re_\tau =180$, (b) $\theta +90^\circ$ at $Re_\tau =6000$, (c) $100\lambda _i h/u_\tau$ at $Re_\tau =180$, (d) $100\lambda _i h/u_\tau$ at $Re_\tau =6000$.

As these unstable eigenmodes are surface waves with $\beta h < \alpha h$, their exponential growth is not directly responsible for the enhancement of streamwise-elongated VLSMs found in free-surface open-channel flows (Di et al. 2019; Duan et al. 2020). It is known that surface waves can enhance VLSMs through the nonlinear Craik–Leibovich mechanism (Craik & Leibovich 1976) when the surface waves are strong enough. However, the exponential growth rates of these unstable eigenmodes are small. For example, the imaginary part of the eigenvalue for the most unstable eigenmode is $\lambda _i h / u_\tau \approx 0.07$ at $Fr_\tau = 0.142$ and $Re_\tau = 6000$, and the corresponding exponential growth rate of the perturbation energy $\exp (2 \lambda _i t)$ is equal to $\exp (0.14 tu_\tau /h)$. The maximum value of $t_{max}$, the time when the maximum transient growth is reached, slightly increases with the Reynolds number from $1.8 h / u_\tau$ at $Re_\tau = 180$ to $2.4 h / u_\tau$ at $Re_\tau = 6000$ (see Appendix A), comparable with the time required for the growth of very-large-scale streaks (Hwang & Bengana 2016). During the time scale of the growth of very-large-scale streaks, the exponential growth rate of the unstable surface wave is less than $1.25$. In fact, the features of Langmuir-type flow driven by the nonlinear Craik–Leibovich mechanism, such as the disrupted logarithmic layer (Deng et al. 2019; Peruzzi et al. 2021), have not been reported in free-surface open-channel flows without externally generated waves. Therefore, these unstable surface-wave eigenmodes cannot grow sufficiently to influence VLSMs through the nonlinear Craik–Leibovich mechanism.

The above analyses suggest that compared with the linear instability induced by the free surface, the effect of the free surface on non-modal transient growth is more closely associated with the amplification of VLSMs by the free surface. This result is consistent with the findings in other canonical wall-bounded turbulence, that the non-modal transient growth is crucial for the generation of very-large-scale streaks (Hwang & Bengana 2016; Cossu & Hwang 2017). The mechanism of free surfaces influencing the transient growth rate is analysed in detail in § 4 below.

4. Effects of the free surface on streamwise-elongated motions

In this section, we investigate the mechanisms by which the free surface affects the transient growth of streamwise-elongated ($\alpha h \ll \beta h$) motions. The mechanism for streamwise-uniform ($\alpha h = 0$) motions is first investigated in § 4.1, and the effects of the Froude number $Fr_\tau$ and the spanwise wavenumber $\beta h$ at different Reynolds numbers are examined. Then, in § 4.2, the mechanism is extended to streamwise-varying motions to show the influence of the streamwise wavenumber $\alpha h$.

4.1. Streamwise-uniform motions

In this section, we conduct transient growth analyses of motions that are uniform in the streamwise direction, i.e. $\alpha h = 0$. The case with $Re_\tau =180$, $Fr_\tau =0.142$, $\alpha h =0$ and $\beta h=1$ is used as an example to illustrate the results. We first show the influence of the free surface on the eigenvalues, eigenmodes and energy growth rate. The budget equation of the perturbation energy is analysed to elucidate the dynamic mechanism underlying how the free surface influences the energy growth rate. Then, we derive the initial conditions of the flow field and the free-surface elevation that enhance the energy transient growth rate. Finally, the mechanism is used to explain the variation in the free-surface effect on the energy transient growth rate with the Froude number and the spanwise wavenumber at different Reynolds numbers.

4.1.1. Surface-wave eigenmodes and their impacts on energy growth

Figure 10(a) shows the eigenvalues in the free-surface open channel at $Re_\tau =180$, $Fr_\tau =0.142$, $\alpha h =0$ and $\beta h=1$. The eigenvalues in the corresponding rigid-lid open channel at the same wavenumber and Reynolds number are also plotted in figure 10(a) for comparison. There are two additional eigenvalues in the free-surface open channel case compared with the rigid-lid open channel case. These two additional eigenvalues and the corresponding eigenmodes induced by the free surface are referred to as the ‘surface-wave eigenvalues’ and ‘surface-wave eigenmodes’, respectively, while the other eigenvalues and eigenmodes are called the ‘shear eigenvalues’ and ‘shear eigenmodes’, respectively (Yih 1972). In contrast to the zero values of the real parts of the eigenvalues of the shear eigenmodes, $\lambda _r=0$, the two surface-wave eigenmodes have the same imaginary parts $\lambda _i$ but opposite non-zero real parts $\lambda _r$, indicating that the two surface-wave eigenmodes propagate in opposite spanwise directions with identical phase speeds $|\lambda _r/\beta |$ and the same damping rate $\lambda _i$. Here, $|\lambda _r|$ represents the frequency of the surface-wave eigenmodes. The velocity moduli of the two surface-wave eigenmodes have the same vertical profiles. Figure 10(b) shows the profiles of the velocity moduli $|\bar {u}|$, $|\bar {v}|$ and $|\bar {w}|$ of the surface-wave eigenmodes. The streamwise velocity modulus $|\bar {u}|$ is non-zero due to the presence of the non-uniform base flow $U(y)$, and a viscous Stokes layer appears in the profiles of $|\bar {u}|$ and $|\bar {w}|$ near the bottom. The modulus of the vertical velocity $|\bar {v}|$ increases monotonically with $y$, reaching its maximum value at the surface and inducing surface deformation, which is another distinct feature of surface-wave eigenmodes compared with shear eigenmodes (Yih 1972).

Figure 10. (a) Comparison of eigenvalues $\lambda$ between the free-surface open channel with $Fr_\tau =0.142$ and the rigid-lid open channel. The points represent the eigenvalues of the shear eigenmodes in the free-surface open channel, the diamonds represent the eigenvalues of the surface-wave eigenmodes in the free-surface open channel and the hollow circles represent the eigenvalues in the rigid-lid open channel. (b) Vertical profiles of the velocity moduli of the surface-wave eigenmodes. The results are obtained at $Re_\tau =180$, $\alpha h =0$ and $\beta h=1$.

The surface-wave eigenmodes induced by the free surface have significant effects on the transient growth of the total energy $E$ and kinetic energy $E_{K}$. Figure 11 shows the evolution of $E(t)/E^{in}$ and $E_K(t)/E_K^{in}$ with time. The results are compared among the rigid-lid open channel, free-surface open channel ($Fr_\tau =0.142$) with surface-wave eigenmodes, and free-surface open channel ($Fr_\tau =0.142$) without surface-wave eigenmodes at $Re_\tau =180$, $\alpha h=0$ and $\beta h =1$. In each case, the initial input perturbations are those that lead to the homologous maximum transient growth rates. As shown in figure 11(a), in the rigid-lid case, $E(t)/E^{in}$ initially increases monotonically with time due to the non-orthogonality of the eigenmodes; then the maximum value $G_{max}$ is reached at $tu_\tau / h \approx 1.5$; and finally, $E(t)/E^{in}$ decreases because the eigenmodes are stable. For the free-surface open channel case, when the surface-wave eigenmodes are excluded, $E(t)/E^{in}$ is the same as in the rigid-lid case, indicating that the surface elevation induced by the shear eigenmodes is negligible. In contrast, when the surface-wave eigenmodes are considered, $E(t)/E^{in}$ increases with oscillations for $0< tu_\tau / h <1.5$. The oscillation period is close to the period of the surface-wave eigenmodes $T=2{\rm \pi} h/(|\lambda _r|u_\tau )=1.05 h/u_\tau$ (see $|\lambda _r|$ in figure 10a). Accompanied by the oscillation, $E(t)/E^{in}$ is larger in the free-surface open channel case with surface-wave eigenmodes than in the other two cases for most of the duration $0< tu_\tau /h<1.5$. The above comparison of $E(t)/E^{in}$ among the three cases indicates that the surface-wave eigenmodes are responsible for the larger $G_{max}$ in the free-surface open channel than in the rigid-lid open channel.

Figure 11. Comparisons of (a) $E(t)/E^{in}$ and (b) $E_K(t)/E_K^{in}$ among the rigid-lid open channel flow, free-surface open channel flow ($Fr_\tau =0.142$) with surface-wave eigenmodes and free-surface open channel flow ($Fr_\tau =0.142$) without surface-wave eigenmodes. Note that the curves in the first case and the third case overlap. The results are obtained at $Re_\tau =180$, $\alpha h =0$ and $\beta h=1$, with the initial perturbations leading to $G_{max}$.

The temporal development of the kinetic energy $E_K(t)/E_K^{in}$ is also considerably influenced by the surface-wave eigenmodes. As shown in figure 11(b), when the surface-wave eigenmodes are excluded, $E_K(t)/E_K^{in}$ in the free-surface open channel is equal to $E_K(t)/E_K^{in}$ (which is equal to $E(t)/E^{in}$) in the rigid-lid open channel (figure 11a). However, when the surface-wave eigenmodes in the free-surface open channel are included, $E_K(t)/E_K^{in}$ oscillates with a value larger than $E(t)/E^{in}$ shown in figure 11(a). The maximum value of $E_K(t)/E_K^{in}$ in the free-surface open channel case is approximately 27 % larger than that in the rigid-lid open channel case. Similar to the analyses of $G_K$ (figure 5) based on the relationship in (3.1), the ratio of the kinetic energy to the total energy satisfies $R_K^{in}< R_K(t)\leq 1$, implying that the larger value of $E_K(t)/E_K^{in}$ than $E(t)/E^{in}$ is correlated with the initial potential energy induced by the surface-wave eigenmodes. This result is confirmed by the analyses in the next section.

4.1.2. Impact of surface-wave eigenmodes on the energy budget

Next, the governing equations of the total perturbation energy and kinetic energy are derived and analysed to elucidate how the surface-wave eigenmodes affect the maximum transient growth rate. By applying the dot product of $\boldsymbol {{u}}$ on both sides of (2.2), integrating over the whole open channel and over time, and replacing the surface pressure with the surface boundary condition (2.7), we derive that

(4.1)\begin{equation} \frac{E(t)}{E^{in}} = 1+ \frac{P(t)}{E^{in}} + \frac{S(t)}{E^{in}}+ \frac{V(t)}{E^{in}} +\frac{\epsilon(t)}{E^{in}}. \end{equation}

In (4.1), $P$, $S$, $V$ and $\epsilon$ refer to the integrals of the energy production term, the surface energy transfer term, the non-constant eddy viscosity term and the viscous dissipation term, respectively. They are defined as

(4.2)\begin{gather} P(t)={-}\int_0^t\int_0^h {\overline{uv}} U^\prime\,{\rm d} y\,{\rm d}t, \end{gather}

(4.3)\begin{gather} S(t)=\int_0^t\left[-\nu{\frac{\partial \overline{vv}}{\partial y}}+ \frac{1}{2}\nu_T \frac{\partial \overline{u_iu_i}}{\partial y} \right]_{y=h}\,{\rm d}t, \end{gather}

(4.4)\begin{gather} V(t)= \int_0^t\int_0^h {\frac{\partial \nu_T}{\partial y}}\left({\frac{\partial \overline{vv}}{\partial y}+\frac{1}{2} \frac{\partial \overline{u_iu_i}}{\partial y}}\right)\,{\rm d} y\,{\rm d}t, \end{gather}

(4.5)\begin{gather} \epsilon(t)={-} \int_0^t\int_0^h {\nu_T \overline{\frac{\partial {u_i}}{\partial x_j} \frac{\partial {u_i}}{\partial x_j}}}\,{\rm d} y\,{\rm d}t. \end{gather}

The overline denotes averaging over the horizontal plane. The term $S$ is zero in the rigid-lid open channel flow. For a given wavenumber, $(u_i, \eta ) = (\hat {u}_i,\hat {\eta }) \exp ({{\rm i}(\alpha x +\beta z-\lambda t)})+{\rm c.c.}$

Figure 12(a) shows the time evolution of the budget terms normalised by $E^{in}$ in (4.1) at $Re_\tau =180$, $\alpha h =0$, $\beta h =1$ and $Fr_\tau =0.142$. The vertical dashed line indicates the time at which the maximum transient growth rate is reached. In contrast to common expectations, the contribution of the surface transfer term $S$ to the total energy growth is negligible in the free-surface open channel case, although the surface is deformable. The non-uniform eddy viscosity term $V$ is also negligible in both the rigid-lid and free-surface open channel cases, because it works as a turbulent diffusion term in the transport of turbulent kinetic energy. Therefore, the transient growth rates in the two cases are governed by the net effect of the other two terms, the production term $P$ and the dissipation term $\epsilon$.

Figure 12. Time evolution of the budget terms (4.1) and their components (4.7) and (4.9) normalised by $E^{in}$ in the rigid-lid open channel (red dashed lines with symbols) and free-surface open channel (black solid lines with symbols) cases. The results are obtained at $Re_\tau =180$, $\alpha h =0$ and $\beta h=1$, with the initial input perturbations leading to $G_{max}$. For the free-surface open channel, $Fr_\tau =0.142$.

The effect of the free surface on the balance between the energy production term $P$ and the dissipation term $\epsilon$ is investigated next. Assume that the perturbation consists of a surface-wave part and a shear part, i.e.

(4.6)\begin{equation} ({{u_i}}, {\eta})=({{u_i}}_w+{{u_i}}_s, {\eta}_w+{\eta}_s). \end{equation}

The subscript ‘$w$’ denotes the surface-wave part, which is a linear combination of the surface-wave eigenmodes, and the subscript ‘$s$’ refers to the shear part, which is a linear combination of the shear eigenmodes. Correspondingly, $P$ and $\epsilon$ can also be decomposed into a surface-wave part, a shear part and an interaction part, i.e.

(4.7)\begin{equation} P={-}\int_0^t\int_0^h {\left(\overline{{u_w}{v_w}} +\overline{{u_s}{v_s}} +\overline{{u_s}{v_w}+{u_w}{v_s}}\right) U^\prime}\,{\rm d} y\,{\rm d}t=P_w + P_s + P_{inter}, \end{equation}

and

(4.8)\begin{align} \epsilon&={-} \int_0^t\int_0^h {\nu_T \left(\overline{\frac{\partial {u_i}_w}{\partial x_j} \frac{\partial {u_i}_w}{\partial x_j}}+ \overline{\frac{\partial {u_i}_s}{\partial x_j} \frac{\partial {u_i}_s}{\partial x_j}}+\overline{\frac{\partial {u_i}_w}{\partial x_j} \frac{\partial {u_i}_s}{\partial x_j}+\frac{\partial {u_i}_s}{\partial x_j} \frac{\partial {u_i}_w}{\partial x_j}}\right)}\,{\rm d} y\,{\rm d}t \end{align}

(4.9)\begin{align} &=\epsilon_w + \epsilon_s + \epsilon_{inter}. \end{align}

The interaction parts, denoted by the subscript ‘inter’, exist because the eigenmodes are non-normal. For the rigid-lid case, the surface-wave part and the interaction part do not exist, and thus, $P=P_s$ and $\epsilon =\epsilon _s$.

For the shear part, figure 12(b) shows that the magnitudes of $P_s$ and $\epsilon _s$ normalised by $E^{in}$ are slightly smaller in the free-surface open channel than in the rigid-lid open channel, and $P_s+\epsilon _s$ is comparable between these two cases. Therefore, the free surface has an insignificant effect on the contribution of the shear part to the energy growth rate $E(t)/E^{in}$.

For the surface-wave part, as illustrated in figure 12(c), the surface wave gains little energy from the base flow because the surface-wave part of the energy production term $P_w$ is nearly zero. The dissipation $\epsilon _w$ is negative, consistent with the negative imaginary parts of the eigenvalues $\lambda _i$ in figure 10(a). Consequently, the combined surface-wave part $P_w+\epsilon _w$ has a negative contribution to the energy growth rate $E(t)/E^{in}$. However, when the surface-wave part is present, figure 12(d) shows that the net contribution of the interaction between the surface-wave part and the shear part, $P_{inter}+\epsilon _{inter}$, oscillates with mainly positive values, and the magnitude of this term is greater than $P_w+\epsilon _w$. Therefore, the presence of the surface-wave part increases the energy growth rate $E(t)/E^{in}$ through the interaction part.

Due to the small magnitude of $\epsilon _{inter}$, the quasi-positive contribution of the interaction part to $E(t)/E^{in}$ occurs due to $P_{inter}$ (figure 12d). The interaction production term $P_{inter}$ can be decomposed as follows:

(4.10)\begin{equation} P_{inter} = P_{inter1} + P_{inter2} ={-}\int_0^t\overline{{u}_s{v}_w}U^\prime \,{\rm d} y\,{\rm d}t -\int_0^t\overline{{u}_w{v}_s}U^\prime \,{\rm d} y\,{\rm d}t. \end{equation}

As shown in figure 13, $P_{inter}$ is dominated by $P_{inter1}$, i.e.

(4.11)\begin{equation} P_{inter} \approx P_{inter1} ={-}\int_0^t\overline{{u}_s{v}_w}U^\prime \,{\rm d} y\,{\rm d}t . \end{equation}

This is because among the four velocity components in (4.10), only $u_s$ increases with time (shown below). In conclusion, the free surface leads to the amplification and oscillation of $E(t)/E^{in}$ due to the energy production, which is related to the interaction between the vertical velocity of the surface-wave part $v_w$ and the streamwise velocity of the shear part $u_s$. The effect of the interaction production term is also confirmed at $Re_\tau =6000$ in Appendix B.

Figure 13. Decomposition of $P_{inter}$ (4.10) obtained at $Re_\tau =180$, $Fr_\tau =0.142$, $\alpha h =0$ and $\beta h=1$.

The governing equation of the kinetic energy $E_K(t)/E_K^{in}$ can be derived from (4.1) as

(4.12)\begin{equation} \frac{E_K(t)}{E_K^{in}} = 1+\frac{P+S+V+\epsilon}{E_K^{in}}+\frac{E_\eta^{in}-E_\eta(t)}{E_K^{in}}. \end{equation}

The second term on the right-hand side of (4.12),

(4.13)\begin{equation} \frac{P+S+V+\epsilon}{E_K^{in}} =\frac{P+S+V+\epsilon}{E^{in}R_K^{in}}, \end{equation}

represents the net contribution of the energy production, surface energy transfer, and the effects of non-uniform eddy viscosity and dissipation. The third term, $(E_\eta ^{in}-E_\eta (t))/{E_K^{in}}$, represents the transformation of potential energy to kinetic energy. Figure 14 shows the time evolution of the budget terms in (4.12), with the term $(P+S+V+\epsilon )/E^{in}$ included for comparison. The results demonstrate that $(P+S+V+\epsilon )/E_K^{in}$ is larger than $(P+S+V+\epsilon )/E^{in}$, indicating the large initial potential energy $E_\eta ^{in}$. In addition, $(E_\eta ^{in}-E_\eta (t))/{E_K^{in}}$ is positive and oscillates at a period equal to half of the period of the surface-wave eigenmodes $T=1.05h/u_\tau$, suggesting that the initial potential energy is associated with the surface-wave part.

Figure 14. Time evolution of the budget terms in (4.12). The results are obtained in a free-surface open channel at $Re_\tau =180$, $\alpha h =0$, $\beta h=1$ and $Fr_\tau =0.142$.

The above analyses of the energy budget equation show that the initial surface-wave part contains considerable potential energy $E_\eta ^{in}$ and interacts with the shear part, leading to a maximum in the quasi-positive energy production term. This in turn leads to greater values of $G_{max}$ and $G_K$ in the free-surface case than in the rigid-lid case, as shown in figures 3–7.

4.1.3. Initial fields that enhance the energy growth rate of streamwise-uniform motions

Next, we study the state of the initial flow, especially the phase relationship between the surface-wave part and the shear part, which can maximise the energy production term $P_{inter1}/E^{in}$ in (4.11).

Figure 15 displays the flow fields, surface deformation, and their shear and surface-wave parts at $t=iT/4$, with $i=0,1,\ldots,6$. Here, $T$ is the period of the two surface-wave eigenmodes corresponding to the frequency $|\lambda _r|$ in figure 10(a), which equals $1.05h/u_\tau$. The initial flow field consists of a pair of strong streamwise vortices denoted by the vector $(v,w)$ and relatively weak streaks of streamwise velocity $u$, with an apparent surface elevation $\eta$ (figure 15a i). The initial $(v,w)$ originates from the shear part $(v_s,w_s)$ (figure 15b i), because the initial vertical and spanwise velocities contributed by the surface-wave part are approximately zero, i.e. $v_w\approx 0$ and $w_w\approx 0$ (figure 15c i). The initial streamwise velocity $u$ (figure 15a i) is contributed by the shear part $u_s$ (figure 15b i) and the relatively weak surface-wave part $u_w$, which have opposite signs (figure 15c i). The initial surface deformation $\eta$ is determined by the surface-wave part $\eta _w$ (figure 15a i,c i). The zero initial vertical and spanwise velocities under the obvious spanwise wave (figure 15c i) indicate that the surface wave is not a progressive wave but rather a standing wave composed of two surface-wave eigenmodes with the same frequency propagating in opposite directions (figure 10a). This finding is confirmed by the time evolution of the surface deformation of the surface-wave part (figure 15c i–c vii). The surface elevation of the initial standing wave is in phase with the streamwise velocity generated by the lifting-up of the mean shear by streamwise vortices.

Figure 15. Velocity field and surface elevation, as well as their shear and surface-wave parts, at (a i–c i) $t=0$, (a ii–c ii) $t=T/4$, (a iii–c iii) $t=T/2$, (a iv–c iv) $t=3T/4$, (a v–c v) $t=T$, (a vi–c vi) $t=5T/4$ and (a vii–c vii) $t=3T/2$. Panels (a i–a vi) show the total, panels (b i–b vii) depict the shear part and panels (c i–c vii) display the surface-wave part. Here, $T$ is the period of the two surface-wave eigenmodes, and the maximum transient growth is reached at $t=3T/2$. The vector is composed of the vertical and spanwise velocities, and the contours are the streamwise velocity.

Over time, the streamwise vortices (figure 15b i–b vii) in the shear part attenuate to amplify the streamwise velocity $u_s$, similar to the generation of streaks by the lifting-up effect in closed channel flows (Pujals et al. 2009). Moreover, due to the small negative value of $\lambda _i$ for the two surface-wave eigenmodes (figure 10a), the magnitudes of the surface elevation and the velocity fields induced by the standing wave attenuate slowly and oscillate (figure 15c i–c vii), which is consistent with the oscillation of the positive $(E_\eta ^{in}-E_\eta (t))/{E_K^{in}}$ term in figure 14. Combining the two parts, the amplified flow field at the time when $G_{max}$ is reached is featured by strong streaks (figure 15a vii). Therefore, the streaks are amplified at the expense of the initial streamwise vortices and the standing wave in the free-surface open channel.

It can be proven that only the initial state of the surface-wave part shown in figure 15(c i) can maximise the energy production term $P_{inter1}/E^{in}$, which is correlated with the interaction between the surface-wave part and the shear part (4.11). For the shear part, the shear eigenmodes have $\lambda _r$ values of zero (figure 10a), i.e. zero frequency. The distribution of the shear part in the $y\unicode{x2013}z$ plane is similar at different times, with the magnitude varying with time (figure 15b i–b vii). In particular, the locations of the streamwise vortices and streaks do not change with time. However, the magnitudes of the streamwise vortices decrease with time, and the intensity of the streaks increases with time. Therefore, the velocities of the shear part can be assumed to be

(4.14)\begin{gather} u_s=f_{us}(y)g(t)\cos(\beta z + \theta_s), \end{gather}

(4.15)\begin{gather} v_s={-}f_{vs}(y)m(t)\cos(\beta z + \theta_s), \end{gather}

(4.16)\begin{gather} w_s={-}f_{ws}(y)n(t)\sin(\beta z + \theta_s). \end{gather}

Here, $f_{us}$ and $f_{vs}$ are positive, and the sign of $f_{ws}$ changes near the channel centre. The time functions satisfy $g(t)\geq 1$, $m(t)\leq 1$ and $n(t)\leq 1$, with $g(0)= m(0)= n(0)= 1$. The angle $\theta _s$ indicates the phase of the shear part in the spanwise direction.

The surface-wave part is a linear combination of the two surface-wave eigenmodes, i.e.

(4.17)\begin{gather} u_w = f_{uw}(y)\left[{-}a_1 \sin(\beta z +|\lambda_r| t+\theta_{w1} ) + a_2 \sin(\beta z - |\lambda_r| t+ \theta_{w2})\right] {\rm e}^{\lambda_i t}, \end{gather}

(4.18)\begin{gather} v_w = f_{vw}(y)\left[a_1 \cos(\beta z +|\lambda_r| t+\theta_{w1} ) + a_2 \cos(\beta z - |\lambda_r| t+ \theta_{w2})\right] {\rm e}^{\lambda_i t}, \end{gather}

(4.19)\begin{gather} w_w = f_{ww}(y)\left[{-}a_1 \sin(\beta z +|\lambda_r| t+\theta_{w1} ) - a_2 \sin(\beta z - |\lambda_r| t+ \theta_{w2})\right] {\rm e}^{\lambda_i t}, \end{gather}

(4.20)\begin{gather} \eta_w = f_{\eta}\left[a_1 \sin(\beta z +|\lambda_r| t+\theta_{w1} ) - a_2 \sin(\beta z - |\lambda_r| t+ \theta_{w2})\right] {\rm e}^{\lambda_i t}, \end{gather}

where $f_{uw}(y)$, $f_{vw}(y)$ and $f_{ww}(y)$ are the moduli of the surface-wave eigenmodes (figure 10b) and $\theta _{w1}$ and $\theta _{w2}$ are the phases of the two surface-wave eigenmodes. Note that $\lambda _i$ and $\lambda _r$ are the attenuation rate and frequency of the surface-wave eigenmodes, respectively (figure 10a), and $f_{\eta }$ is the surface elevation in the eigenmodes. The parameters $a_1$ and $a_2$ are positive. We assume that for the surface-wave part, the small phase change in the vertical velocity of the surface-wave eigenmodes can be ignored. The phase relationships $\theta _s-\theta _{w1}$ and $\theta _s-\theta _{w2}$, and the relationship between $a_1$ and $a_2$ needed to maximise $P_{inter1}/E^{in}$ are derived below.

Here, $P_{inter1}$ (4.11) can be approximated as

(4.21)\begin{align} P_{inter1}&\approx{-}\frac{1}{2} F \sum_{n=0}^N \frac{\varPhi^{(n)}(0)}{|\lambda_r| n! } t^{n}(a_1\sin(|\lambda_r| t+\theta_{w1}-\theta_{s})+a_2\sin(|\lambda_r| t+\theta_{s}-\theta_{w2})\nonumber\\ &\quad + \frac{a_1F\sin(\theta_{w1}-\theta_s) +a_2F\sin(\theta_{s}-\theta_{w2})}{2|\lambda_r|}, \end{align}

with

(4.22)\begin{equation} F=\int_0^hf_{us}(y)f_{vw}(y) U^\prime \,{\rm d} y \end{equation}

and

(4.23)\begin{equation} \varPhi (t)=g(t){\rm e}^{\lambda_i t}. \end{equation}

Here, $\varPhi ^{(n)}(0)$ is the $n$th derivative of $\varPhi$ at $t=0$. Equation (4.21) is obtained based on the Taylor expansion of $\varPhi$ at $t=0$. The first term on the right-hand side of (4.21) is responsible for the oscillation of $P_{inter1}$, and the second term is a constant. When $\theta _{w1}-\theta _s={\rm \pi} /2$ and $\theta _{s}-\theta _{w2}={\rm \pi} /2$, the second term reaches its positive maximum value, which leads to a quasi-positive $P_{inter}$. Under such conditions,

(4.24)\begin{equation} P_{inter1}={-}\frac{(a_1+a_2)F}{2} \sum_{n=0}^N \frac{\varPhi^{(n)}(0)}{|\lambda_r| n! } t^{n}\sin(|\lambda_r| t+{\rm \pi}/2)+\frac{(a_1+a_2)F}{2|\lambda_r|}. \end{equation}

For specified $Re_\tau$, $Fr_\tau$, $\alpha h$ and $\beta h$, the values of $F$, $\lambda _r$ and $\varPhi ^{(n)}(0)$ are constant. The maximum value of $P_{inter1}$ increases with $a_1+a_2$.

To obtain the maximal $P_{inter}/E^{in}$, the relationship between $a_1$ and $a_2$ that minimises $E^{in}$ must be determined. Keeping the shear part constant, $a_1$ and $a_2$ should be chosen to minimise the sum of the surface-wave part of the kinetic energy $(E_K)_w^{in}$, the interaction part of the kinetic energy $(E_K)_{inter}^{in}$ and the surface-wave part of the potential energy $(E_\eta )_w^{in}$. The interaction part of the potential energy is ignored because the surface deformation of the shear part is negligible. With $\theta _{w1}-\theta _s={\rm \pi} /2$ and $\theta _{s}-\theta _{w2}={\rm \pi} /2$, the energy $(E_K)_w^{in} + (E_K)_{inter}^{in}+(E_\eta )_w^{in}$ contributed by the surface-wave eigenmodes is

(4.25)\begin{align} & (E_K)_w^{in} + (E_K)_{inter}^{in} + (E_\eta)_w^{in} =\frac{(a_1+a_2)^2}{2} \left(\int_0^{h} f_{uw}^2(y)\,{\rm d} y + f_{\eta}^2\right)\nonumber\\ &\qquad -2(a_1+a_2)\int_0^hf_{uw}(y)f_{us}(y)\,{\rm d} y\nonumber\\ &\qquad + \frac{(a_1-a_2)^2}{2} \int_0^{h} f_{vw}^2(y)+f_{ww}^2(y)\,{\rm d} y. \end{align}

Because $a_1$, $a_2$ and $f_{uw}(y)f_{us}(y)$ are positive and $f_{uw}< f_{ww}$, $a_1=a_2$ minimises $(E_K)_w^{in} + (E_K)_{inter}^{in} + (E_\eta )_w^{in}$ as

(4.26)\begin{equation} (E_K)_w^{in} + (E_K)_{inter}^{in} + (E_\eta)_w^{in}=2a_1^2 \left(\int_0^{h} f_{uw}^2(y)\,{\rm d} y + f_{\eta}^2\right)-4a_1\int_0^hf_{uw}(y)f_{us}(y)\,{\rm d} y, \end{equation}

which is finally determined by $a_1$.

Therefore, under the conditions of $a_1=a_2$, $\theta _{w1}-\theta _s={\rm \pi} /2$ and $\theta _{s}-\theta _{w2}={\rm \pi} /2$, the final analytical result of $P_{inter1}/E^{in}$ is

(4.27)\begin{equation} \frac{P_{inter1}}{E^{in}}=\frac{-\dfrac{a_1F}{|\lambda_r|} \left(\sum_{n=0}^N \dfrac{\varPhi^{(n)}(0)}{ n! } t^{n}\sin(|\lambda_r| t+{\rm \pi}/2)-1\right)}{2a_1^2 \left(\int_0^{h} f_{uw}^2(y)\,{\rm d} y + f_{\eta}^2\right)-4a_1\int_0^hf_{uw}(y)f_{us}(y)\,{\rm d} y + (E_K)_s^{in}}, \end{equation}

which is a function of $a_1$ and $t$ for specified Reynolds number, Froude number and wavenumber. For the maximum $P_{inter1}/E^{in}$, the value of $a_1$ can be obtained from $\partial (P_{inter1}/E^{in})/\partial a_1=0$.

Note that when $a_1=a_2$, $\theta _{w1}-\theta _s={\rm \pi} /2$ and $\theta _{s}-\theta _{w2}={\rm \pi} /2$, the velocities and surface elevation perturbations of the surface-wave part satisfy

(4.28)\begin{gather} u_w ={-}2 a_1 f_{uw}(y) \cos(\beta z +\theta_s) \cos(|\lambda_r| t) {\rm e}^{\lambda_i t}, \end{gather}

(4.29)\begin{gather} v_w ={-}2 a_1 f_{vw}(y) \cos(\beta z +\theta_s) \sin(|\lambda_r| t) {\rm e}^{\lambda_i t}, \end{gather}

(4.30)\begin{gather} w_w = 2 a_1 f_{ww}(y) \sin(\beta z +\theta_s) \sin(|\lambda_r| t){\rm e}^{\lambda_i t}, \end{gather}

(4.31)\begin{gather} \eta = 2 a_1 f_{\eta} \cos(\beta z +\theta_s) \cos(|\lambda_r| t){\rm e}^{\lambda_i t}, \end{gather}

which represent a standing wave, as shown in figures 15(c i)–15(c vii).

4.1.4. Effects of the spanwise wavenumber and Froude number at different Reynolds numbers

The above analyses indicate that the free surface enhances the transient growth rate through the interaction production term $P_{inter}$ (4.11). Next, we confirm this mechanism at different spanwise wavenumbers, Froude numbers and Reynolds numbers, and explain the variation in the free-surface effect on the transient growth rate of streamwise-uniform motions with different spanwise wavenumbers and Froude numbers.

Figure 16 shows a comparison of the time histories of the interaction production term $P_{inter}$ at different Froude numbers and spanwise wavenumbers for $Re_\tau =180$, $360$ and $1000$. The term $P_{inter}$ increases with increasing $Fr_\tau$ but decreases sharply with increasing spanwise wavenumber $\beta h$. For the same Froude number and spanwise wavenumber, the change in $P_{inter}$ with the Reynolds number is negligible. Recall that at three different Reynolds numbers $Re_\tau =180$, $360$ and $1000$, the free-surface effects on the transient growth rate are similar (figures 5 and 7), increasing with increasing Froude number but attenuating obviously with increasing spanwise wavenumber. Thus, the variation in $P_{inter}$ with the Froude number and spanwise wavenumber is consistent with the variation in the transient growth rate with these parameters, confirming that the interaction production term is an important mechanism underlying that the free surface influences the transient growth of motions.

Figure 16. Time evolution of the interaction production term $P_{inter}$ (a i–c i) at different Froude numbers $Fr_\tau$ for $\alpha h = 0$ and $\beta h=1$ and (a ii–c ii) at different spanwise wavenumbers $\beta h$ for $Fr_\tau =0.142$ and $\alpha h = 0$. The results are obtained at (a i,a ii) $Re_\tau =180$, (b i,b ii) $Re_\tau =360$ and (c i,c ii) $Re_\tau =1000$.

The variations in $P_{inter}$ and the transient growth rate with the Froude number and spanwise wavenumber can be explained using the analytical expression of the production term (4.27). The interaction production term $P_{inter}$ decreases as the frequency of the surface-wave eigenmodes $|\lambda _r|$ increases. Additionally, $P_{inter}$ in (4.27) is proportional to the integral term $F$ (4.22) associated with the vertical velocity modulus of the surface-wave eigenmodes. The variations in the frequency and vertical velocity modulus of the surface-wave eigenmodes with the Froude number and spanwise wavenumber are shown in figure 17. The frequency of the surface-wave eigenmodes decreases with increasing Froude number, whereas the vertical velocity modulus does not change with the Froude number. Therefore, an increase in the Froude number leads to an increase in $P_{inter}$ (figure 16a i–c i), and this escalation can be attributed solely to the decrease in the frequency of the surface-wave eigenmodes $|\lambda _r|$. Moreover, an increase in the spanwise wavenumber has dual effects on the surface-wave eigenmodes, increasing their frequency while also reducing the integral term $F$. The integral term $F$ is determined by the product of the streamwise velocity, which is composed of shear eigenmodes, and the vertical velocity, which is composed of surface-wave eigenmodes. As the spanwise wavenumber increases, the moduli of the vertical velocity of the surface-wave eigenmode becomes more concentrated near the free surface and rapidly diminishes away from it. Simultaneously, in the present result (figure 15b i–b vii) and other canonical wall-bounded turbulence (Cossu et al. 2009), the streamwise velocity of the perturbation composed of shear eigenmodes is more concentrated near the bottom wall. Consequently, the vertical locations where both components are significant start to separate, leading to a reduction in their product and thus a decrease in $F$. Combining with the increase of $|\lambda _r|$, $P_{inter}$ decreases with increasing spanwise wavenumber (figures 16a ii–c ii). Thus, the effect of the free surface on the transient growth rate is significant only for small spanwise wavenumbers at relatively high Froude numbers.

Figure 17. Variations in (a,c) the eigenvalues and (b,d) the vertical velocity modulus of the surface-wave eigenmodes (a,b) with the Froude number $Fr_\tau$ ($Fr_\tau = 0.071, 0.1, 0.142$ and $0.212$) for $\alpha h = 0$ and $\beta h=1$ and (c,d) with the spanwise wavenumber $\beta h$ ($\beta h = 1, 2, 3$ and $4$) for $Fr_\tau =0.142$ and $\alpha h = 0$. The results are obtained at $Re_\tau =180$.

In summary, the free surface affects the transient growth process of streamwise-uniform motions through the interaction between spanwise standing waves consisting of surface-wave eigenmodes and streamwise vortices consisting of shear eigenmodes. In particular, the growth rates of the total energy and kinetic energy are enhanced by the energy extracted from the mean velocity gradient through the correlation between the streamwise velocity induced by the lifting-up effect of the streamwise vortices and the vertical velocity induced by the spanwise standing wave. This occurs if the initial surface elevation of the standing wave is at its maximum and the phase is the same as that of the streamwise velocity induced by the lifting-up effect of the streamwise vortices. The maximal transient growth rate is inversely proportional to the frequency of the standing wave, which decreases with increasing Froude number, but increases with increasing spanwise wavenumber. In the transient growth process, only the energy of the streamwise velocity is amplified, which is at the expense of the attenuation of the streamwise vortices and standing waves. Because the initial flow field tends to trigger the transient growth, the amplified flow field represents commonly observed flow states in turbulence. The amplified flow field is featured by energetic very-large-scale $u$ and relatively weak $v$ and $w$, which is consistent with the results of direct numerical simulations and laboratory experiments of free-surface open channel turbulent flows (Borue et al. 1995; Kumar, Gupta & Banerjee 1998; Duan et al. 2020; Yoshimura & Fujita 2020).

4.2. Effects of the free surface on streamwise-varying motions

The analyses in § 4.1 reveal the mechanism by which the free surface influences the streamwise-uniform motions. As shown in § 3, the maximum growth rate $G_{max}$ in the streamwise-varying case ($\alpha h \neq 0$) is also enhanced by the free surface, although its value is smaller than that of the streamwise-uniform case ($\alpha h = 0$). In this section, the case with $\alpha h=0.2$ and $\beta h =1$ is used as an example to elucidate the reason underlying this result. First, the effects of the surface-wave eigenmodes on the energy growth are analysed. Then, the conditions of the surface wave part and the shear part for enhancing $G_{max}$ are derived based on the features of the surface-wave and shear eigenmodes. The following analyses elucidate the mechanism by which the free surface influences the streamwise-varying motions. In addition, we have confirmed the mechanism for the streamwise-varying motions cases across different wavenumbers, Froude numbers and Reynolds numbers in a manner similar to that for the streamwise-uniform case in § 4.1.4 (see the confirmation by the results at $\alpha h =0.5$, $\beta h=1$ and $Re_\tau =6000$ in Appendix C).

4.2.1. Effect of the free surface on the energy budgets for the streamwise-varying case

Similar to the streamwise-uniform case analysed in § 4.1, the energy growth rate $E(t)/E^{in}$ in the streamwise-varying case is dominated by the difference between the production term and the dissipation term. According to (4.7) and (4.9), the budget terms can be decomposed into a shear part, a wave part and an interaction part, with the latter two associated with the free surface. To examine the net contribution of these three parts to $E(t)/E^{in}$, figure 18(a) illustrates the time evolution of the combination of the shear parts of the production term and dissipation term $(P_{s}+\epsilon _{s})/E^{in}$, the combination of the wave parts of the production term and dissipation term $(P_{w}+\epsilon _{w})/E^{in}$, and the combination of the interaction parts of the production term and dissipation term $(P_{inter}+\epsilon _{inter})/E^{in}$ in the streamwise-uniform case (dashed line with symbols) and the streamwise-varying case (solid line with symbols). As shown, for both the streamwise-varying and streamwise-uniform cases, the net contribution of the wave part is negligible, while the interaction part $(P_{inter}+\epsilon _{inter})/E^{in}$ has a significant positive contribution. As shown in figure 18(b), the net contribution of $(P_{inter}+\epsilon _{inter})/E^{in}$ is due mainly to $P_{inter}$. Further decomposing $P_{inter}$ into $P_{inter1}$ and $P_{inter2}$, as shown in (4.10), we find that $P_{inter}$ is governed by $P_{inter1}$. Therefore, similar to the streamwise-uniform case, the free surface enhances the energy growth rate of the streamwise-varying motions through the energy production term that arises due to the correlation between the streamwise velocity of the shear part and the vertical velocity of the surface-wave part (4.11).

Figure 18. (a) Comparison of the time evolution of the budget terms $(P_{s}+\epsilon _{s})/E^{in}$, $(P_{w}+\epsilon _{w})/E^{in}$, $(P_{inter}+\epsilon _{inter})/E^{in}$ and $E(t)/E^{in}$ (definitions provided in § 4.1.2) between the streamwise-uniform case ($\alpha h = 0$, dashed lines with symbols) and the streamwise-varying case ($\alpha h = 0.2$, solid lines with symbols). (b) Time evolution of the budget terms $P_{inter}$, $P_{inter1}$, $P_{inter2}$ and $\epsilon _{inter}$ in the streamwise-varying case ($\alpha h = 0.2$). The results are obtained at $Re_\tau =180$, $\beta h=1$ and $Fr_\tau =0.142$.

Because the values of $(P_{inter}+\epsilon _{inter})/E^{in}$ in the streamwise-varying and streamwise-uniform cases in figure 18(a) are comparable, the energy growth rate $E(t)/E^{in}$ in the streamwise-varying case is smaller than that in the streamwise-uniform case, mainly due to the smaller net contribution from the shear part $(P_{s}+\epsilon _{s})/E^{in}$. In closed channel flows, the energy growth rate, which is governed by the difference between the shear parts of the production and dissipation terms, also decreases with increasing $\alpha h$ (Cossu et al. 2009).

4.2.2. Initial conditions for the transient growth of streamwise-varying motions

Next, the features of the surface-wave part and shear part in the streamwise-varying case are analysed to study the initial state of the surface-wave part, which can lead to the maximum production term $P_{inter1}/E^{in}$ that is responsible for the enhancement of the energy growth rate by the free surface.

Figure 19 shows the eigenvalues of the surface-wave and shear eigenmodes, and the velocity moduli of the two surface-wave eigenmodes. As shown in figure 19(a), there are two surface-wave eigenmodes with different $\lambda _r$, indicating different propagation speeds $c=\lambda _r/k$ along the wavenumber direction $(\alpha /k, \beta /k)$. The propagation speeds of the two surface-wave eigenmodes are $c_1=c_s+c_w$ and $c_2=c_s-c_w$, with $c_s=(\lambda _{r1}+\lambda _{r2})/(2k)=\lambda _r^s/k$ and $c_w=|\lambda _{r1}-\lambda _{r2}|/(2k)=\lambda _r^w/k$. The velocity $c_s$ is approximately equal to the projection of the surface base flow speed in the wavenumber direction $U(h)\alpha /k$. In addition, the $\lambda _r$ values of the shear eigenmodes are all close to $\lambda _r^s$, implying that the shear part consisting of the shear eigenmodes propagates in the direction of $(\alpha /k, \beta /k)$ at a speed of $c_s=\lambda _r^s/k$. The velocity $c_w$ represents the propagation speed of the surface-wave eigenmodes relative to the shear eigenmodes.

Figure 19. (a) Eigenvalues of the surface-wave eigenmodes (diamonds) and the shear eigenmodes (circles). (b,c) Velocity moduli of the two surface-wave eigenmodes. The surface-wave eigenmode with the larger $\lambda _r$ is shown by lines without symbols, and the other eigenmode is shown by lines with symbols. The velocity moduli are shown in the coordinate system (b) $(x,y,z)$ and (c) $(\tilde {x},\tilde {y},\tilde {z})$. The results are obtained at $Re_\tau =180$, $\alpha h=0.2$, $\beta h=1$ and $Fr_\tau =0.142$.

Based on the propogation directions of the surface-wave eigenmodes and shear eigenmodes, a new coordinate system is defined using the transformation

(4.32)\begin{equation} \tilde{x}= x\frac{\beta}{k} -z \frac{\alpha}{k},\quad \tilde{y}= y,\quad \tilde{z}= z\frac{\beta}{k} +x \frac{\alpha}{k}. \end{equation}

Here, the $\tilde {z}$-axis is parallel to the wavenumber vector. Correspondingly, the velocity components $\tilde {u}_i$ in the new coordinate system $(\tilde {x},\tilde {y},\tilde {z})$ are

(4.33)\begin{equation} \tilde{u}= u\frac{\beta}{k} -w \frac{\alpha}{k},\quad \tilde{v}= v,\quad \tilde{w}= w\frac{\beta}{k} +u \frac{\alpha}{k}. \end{equation}

As shown in figure 19(b), in the coordinate system $(x,y,z)$, the vertical velocity moduli of the two surface-wave eigenmodes are similar, while the streamwise velocity moduli of the two surface-wave eigenmodes are noticeably different. However, in the new coordinate system $(\tilde {x},\tilde {y},\tilde {z})$, the streamwise velocity moduli $|\tilde {u}|$ of the two eigenmodes in the $\tilde {x}$-direction are much closer (figure 19c).

The difference between the exponential damping rates of the two surface-wave eigenmodes, i.e. ${\rm e}^{\lambda _{i1}t}$ and ${\rm e}^{\lambda _{i2}t}$ (figure 19a), is small within the time needed to reach the maximum transient growth rate ($t_{max}\approx 1.5 h/u_\tau$). Therefore, the velocity of the surface-wave part can be approximated as

(4.34)$$\begin{gather} \tilde{u}_w=a_1 f_{\tilde{u}w} \sin(k\tilde{\tilde{z}}+\lambda^w_rt + \theta_{w1}) {\rm e}^{\lambda_{i} t} - a_2 f_{\tilde{u}w} \sin (k\tilde{\tilde{z}}-\lambda^w_rt + \theta_{w2}) {\rm e}^{\lambda_{i} t}, \end{gather}$$

(4.35)$$\begin{gather}\tilde{v}_w=a_1 f_{\tilde{v}w} \cos(k\tilde{\tilde{z}}+\lambda^w_rt+\theta_{w1}) {\rm e}^{\lambda_{i} t} +a_2 f_{\tilde{v}w} \cos (k\tilde{\tilde{z}}-\lambda^w_rt + \theta_{w2}) {\rm e}^{\lambda_{i} t}, \end{gather}$$

(4.36)$$\begin{gather}\tilde{w}_w={-}a_1 f_{\tilde{w}w} \sin(k\tilde{\tilde{z}}+\lambda^w_rt + \theta_{w1}) {\rm e}^{\lambda_{i} t} - a_2 f_{\tilde{w}w} \sin (k\tilde{\tilde{z}}-\lambda^w_rt + \theta_{w2}) {\rm e}^{\lambda_{i} t}, \end{gather}$$

(4.37)$$\begin{gather}\tilde{\eta}_w=a_1 f_{\eta} \sin(k\tilde{\tilde{z}}+\lambda^w_rt + \theta_{w1}) {\rm e}^{\lambda_{i} t} - a_2 f_{\eta} \sin (k\tilde{\tilde{z}}-\lambda^w_rt + \theta_{w2}) {\rm e}^{\lambda_{i} t}. \end{gather}$$

Here, $f_{\tilde {u}w}$, $f_{\tilde {v}w}$, $f_{\tilde {w}w}$, $f_{\eta }$ and $\lambda _{i}$ are approximations of the moduli of $\tilde {u}$, $\tilde {v}$, $\tilde {w}$, $\eta$ and the damping rate of the two surface-wave eigenmodes, respectively, and

(4.38)\begin{equation} \tilde{\tilde{z}}=\tilde{z}-c_st. \end{equation}

The two surface-wave eigenmodes in the streamwise-varying case propagate in opposite $\tilde {\tilde {z}}$-directions at the same phase speed; hence, the surface-wave part has a similar expression to that in the streamwise-uniform case (4.17)–(4.20).

Figure 20 displays the flow field and surface deformation in the transient growth process in the plane $(\tilde {y}=y,\tilde {\tilde {z}}=\tilde {z}-c_st)$, as well as the corresponding shear and surface-wave parts, at $t=iT/4$, with $i=0,1,\ldots,6$. Here, the period $T$ is equal to $2{\rm \pi} /(kc_w)$, and the velocity $c_w$ is the propagation speed of the surface-wave eigenmode relative to the speed of the shear eigenmodes (figure 19a). As shown in figure 20(b i–b vii), the shear part consists of initially strong vortices in the $\tilde {x}$-direction, as evidenced by $(\tilde {v},\tilde {w})$ and the streaks of $\tilde {u}$. As time increases, the vortices decay and the streaks are enhanced. Because the phase speed of the shear eigenmodes in the wavenumber vector direction is approximately $c_s$ (figure 19a), the spanwise locations of the vortices are essentially unchanged in the plane $(\tilde {y}=y,\tilde {\tilde {z}}=\tilde {z}-c_st)$. As a result, the velocities of the shear part can be approximated as

(4.39)\begin{gather} \tilde{u}_s=f_{\tilde{u}s}(\tilde{y})\cos(k\tilde{\tilde{z}} + \theta_s)\tilde{g}(t), \end{gather}

(4.40)\begin{gather} \tilde{v}_s={-}f_{\tilde{v}s}(\tilde{y})\cos(k\tilde{\tilde{z}}+ \theta_s) \tilde{m}(t), \end{gather}

(4.41)\begin{gather} \tilde{w}_s={-}f_{\tilde{w}s}(\tilde{y})\sin(k\tilde{\tilde{z}}+ \theta_s) \tilde{n}(t), \end{gather}

with $\tilde {g}(t)\geq 1$, $\tilde {m}(t)\leq 1$ and $\tilde {n}(t)\leq 1$. The moduli $f_{\tilde {u}s}$ and $f_{\tilde {v}s}$ are positive, while the sign of $f_{\tilde {w}s}(y)$ changes near the channel centre. The shear part in the streamwise-varying case, expressed using $\tilde {y}$ and $\tilde {\tilde {z}}$, is similar to that in the streamwise-uniform case (4.14)–(4.16).

Figure 20. Velocity field ($\tilde {u}$, $\tilde {v}$, $\tilde {w}$) and the surface elevation $\eta$, as well as their shear and surface-wave parts, in the plane $(\tilde {y}=y,\tilde {\tilde {z}}=\tilde {z}-c_st)$ at (a i–c i) $t=0$, (a ii–c ii) $t=T/4$, (a iii–c iii) $t=T/2$, (a iv–c iv) $t=3T/4$, (a v–c v) $t=T$, (a vi–c vi) $t=5T/4$ and (a vii–c vii) $t=3T/2$. Panels (a i–a vii) show the total, panels (b i–b vii) depict the shear part and panels (c i–c vii) display the surface-wave part. Here, $T$ is equal to $2{\rm \pi} /(kc_w)$, where $c_w$ is the propagation speed of the surface-wave eigenmodes relative to that of the shear eigenmodes, and the maximum transient growth rate is reached at $t=3T/2$. The vector is composed of the vertical and spanwise velocities ($\tilde {v}$, $\tilde {w}$), and the contours are the streamwise velocity $\tilde {u}$. The results are obtained at $Re_\tau =180$, $\alpha h=0.2$, $\beta h=1$ and $Fr_\tau =0.142$.

Here, $P_{inter1}$ can be expressed as

(4.42)$$\begin{gather} P_{inter1}= \int_0^h\int_0^t\overline{{u}_s{v}_{w}}U^\prime \,{\rm d}t\,{\rm d} y=\int_0^h\int_0^t \left(\frac{\beta}{k}\overline{{\tilde{u}}_s{\tilde{v}}_{w}}+ \frac{\alpha}{k}\overline{{\tilde{w}}_s{\tilde{v}}_{w}}\right)U^\prime \,{\rm d} t \,{\rm d} y\nonumber\\ \approx\int_0^h\int_0^t \frac{\beta}{k}\overline{{\tilde{u}}_s{\tilde{v}}_{w}}U^\prime \,{\rm d}t\,{\rm d} y. \end{gather}$$

Because the sign of $\tilde {w}_s$ changes in the $y$ (or $\tilde {y}$) direction and the sign of $\tilde {v}_{w}$ remains the same in the $y$ direction, the integral ${\alpha }\overline {{\tilde {w}}_s{\tilde {v}}_{w}}/k$ in the $y$ direction is negligible. Additionally, $\alpha$ is much smaller than $\beta$ for streamwise-elongated motions, which we focus on in the present study. Therefore, the ${\alpha }\overline {{\tilde {w}}_s{\tilde {v}}_{w}}/{k}$ part is ignored. Because ${\tilde {u}}_s$ and ${\tilde {v}}_{w}$ in (4.39) and (4.34) have the same forms as those in the streamwise-uniform case, we obtain following (4.21) that

(4.43) $$\begin{gather} P_{inter1}\approx \frac{\beta}{k}\left(-\frac{1}{2} \tilde{F} \sum_{n=0}^N \frac{\tilde{\varPhi}^n(0)}{|\lambda_r^w| n! } t^{n}(a_1\sin(\lambda_r^w t+\theta_{w1}-\theta_{s})+a_2\sin(\lambda_r^w t+\theta_{s}-\theta_{w2}))\right)\nonumber\\ +\frac{\beta}{k}\frac{a_1\tilde{F}\sin(\theta_{w1}-\theta_s) +a_2\tilde{F}\sin(\theta_{s}-\theta_{w2})}{2|\lambda_r^w|}, \end{gather}$$

with

(4.44)\begin{equation} \tilde{F}=\int_0^hf_{\tilde{u}s}(y)f_{\tilde{v}w}(y) U^\prime \,{\rm d} y \end{equation}

and

(4.45)\begin{equation} \tilde{\varPhi} (t)=\tilde{g}(t){\rm e}^{\lambda_i t}. \end{equation}

Similar to the streamwise-uniform case, the maximum value of $P_{inter1}$ is obtained when $\theta _{w1}-\theta _s={\rm \pi} /2$ and $\theta _{s}-\theta _{w2}={\rm \pi} /2$ are satisfied. Under this condition, the portion of the initial input energy associated with the surface-wave part is

(4.46)$$\begin{gather} (E_K)_w^{in} + (E_K)_{inter}^{in} + (E_\eta)_w^{in} =\frac{(a_1+a_2)^2}{2} \left(\int_0^{h} f_{\tilde{u}w}^2(y)\,{\rm d} y + f_{\eta}^2\right)\nonumber\\ -2(a_1+a_2)\int_0^hf_{\tilde{u}w}(y)f_{\tilde{u}s}(y)\,{\rm d} y + \frac{(a_1-a_2)^2}{2} \int_0^{h}\left( f_{\tilde{v}w}^2(y)+f_{\tilde{w}w}^2(y)\right)\,{\rm d} y. \end{gather}$$

The minimum value is obtained when $a_1\approx a_2$. Because the moduli of the two surface-wave eigenmodes are only approximately the same, i.e. not identical, $a_1$ is not exactly equal to $a_2$.

The above analyses show that in the streamwise-varying case, the maximum $P_{inter1}/E^{in}$ is obtained when $a_1\approx a_2$, $\theta _{w1}-\theta _s={\rm \pi} /2$ and $\theta _{s}-\theta _{w2}={\rm \pi} /2$. Under these conditions, the velocities and surface elevation of the surface-wave part are

(4.47)\begin{gather} \tilde{u}_w \approx{-}2 a_1 f_{\tilde{u}w}(y) \cos(k \tilde{\tilde{z}} +\theta_s) \cos(|\lambda^w_r| t) {\rm e}^{\lambda_i t}, \end{gather}

(4.48)\begin{gather} \tilde{v}_w \approx{-}2 a_1 f_{\tilde{v}w}(y) \cos(k \tilde{\tilde{z}} +\theta_s) \sin(|\lambda^w_r| t) {\rm e}^{\lambda_i t}, \end{gather}

(4.49)\begin{gather} \tilde{w}_w \approx 2 a_1 f_{\tilde{w}w}(y) \sin(k \tilde{\tilde{z}} +\theta_s) \sin(|\lambda^w_r| t) {\rm e}^{\lambda_i t} \end{gather}

and

(4.50)\begin{equation} \eta \approx 2 a_1 f_{\eta} \cos(k \tilde{\tilde{z}} +\theta_s) \cos(|\lambda^w_r| t){\rm e}^{\lambda_i t}. \end{equation}

This solution represents a standing wave in the plane $(\tilde {y},\tilde {\tilde {z}})$ parallel to the wavenumber vector that moves with speed $c_s$ in the wavenumber-vector direction. Initially, the surface elevation of the standing wave is at its maximum value, and its phase is the same as that of $\tilde {u}_s$. The standing wave can be confirmed by the variation in the surface elevation at different times, as shown in figure 20(c i–c vii).

In summary, the above analyses show that for the streamwise-varying case, in a plane parallel to the wavenumber vector moving at a speed equal to the surface mean velocity projected in the wavenumber-vector direction, the two surface-wave eigenmodes propagate in opposite directions at the same speed, and the vortices consisting of the shear eigenmodes are approximately fixed in space. If a standing wave reaches its maximum surface elevation and its phase is identical to that of the streamwise velocity induced by the lifting-up effect of the vortices at the initial time, the transient growth rate can be enhanced by the free surface to a maximal level. In other words, the transient growth rate is enhanced by a standing wave riding on the vortices moving at a speed equal to the projection of the surface mean velocity in the wavenumber direction. While the interaction between the surface-wave part and the shear part can enhance the transient growth rate of the streamwise-varying motions in a way similar to that of streamwise-uniform motions, the growth of the total perturbation energy of the streamwise-varying motions is slower because of the decrease in the transient growth rate of the shear part with increasing streamwise wavenumber.

5. Conclusions

In this study, a linear non-modal analysis is performed to investigate the linear mechanism by which free surfaces influence turbulent motions in open channels with a deformable free surface. We use the generalised Orr–Sommerfeld and Squire equations derived from the Reynolds-averaging equation, with the turbulent mean velocity and eddy viscosity included, in our analyses; therefore, the effects of background turbulence are considered in the present study. Because of the transformation of surface potential energy into kinetic energy in the flow, the growth rate of the total energy is considered. The growth rate is calculated by discretising the generalised Orr–Sommerfeld and Squire equations using a Chebyshev spectral collocation method. The results at $Re_\tau =180$, $360$, $1000$ and $6000$ are analysed to elucidate the mechanism by which the free surface influences the transient growth rate.

As observed from the contours of the maximum energy growth rate $G_{max}$ in the spectral space, the $G_{max}$ value of the streamwise-elongated motions (for which the streamwise wavenumber $\alpha h$ is smaller than the spanwise wavenumber $\beta h$) at small spanwise wavenumbers $\beta h<2.7$ is amplified by the free surface at relatively high Froude numbers. This effect is more obvious when the wavenumber decreases and the Froude number increases. The growth rate of the kinetic energy $E_K$ corresponding to $G_{max}$ is also amplified by the free surface. There are two additional surface-wave eigenmodes in the free-surface open channel case compared with the rigid-lid open channel case. If the surface-wave eigenmodes are ignored, $G_{max}$ in the free-surface open channel is the same as that in the rigid-lid open channel, indicating that the surface-wave eigenmodes are important in the enhancement of $G_{max}$.

The budget equation for the energy growth rate is derived to elucidate the mechanism by which the surface-wave eigenmodes influence the growth rate. The budget analysis indicates that the energy growth rate is determined by the difference between the energy production term and the dissipation term, and the surface energy transfer term is negligible. By decomposing the perturbation term into a shear part consisting of the shear eigenmodes and a surface-wave part consisting of the surface-wave eigenmodes, we discover that the increase in $G_{max}$ is due to the interaction term $P_{inter}$, which involves the correlation between the shear part of the streamwise velocity and the surface-wave part of the vertical velocity. The interaction production term exists owing to the non-orthogonality of the eigenmodes.

In the streamwise-uniform case ($\alpha h =0$), the initial shear part of the flow field consists of a pair of streamwise vortices and relatively weak streaks of streamwise velocity that do not move in the spanwise direction over time, similar to other canonical wall-bounded turbulent flows without free surfaces. The two surface-wave eigenmodes propagate in opposite directions along the spanwise axis. Based on the characteristics of the shear eigenmodes and the surface-wave eigenmodes, an analytical expression of the interaction energy production term is derived (4.27). The maximum value of the interaction energy production term is obtained when the surface wave is a standing wave, for which the surface elevation is initially at its maximum value and the spanwise phase is the same as that of the shear part of the streamwise velocity. According to the derived analytical expression of the interaction energy production term, the increase in $G_{max}$ due to the free surface becomes more pronounced when the frequency of the surface-wave eigenmodes decreases. When the Froude number increases or the spanwise wavenumber decreases, the frequency of the surface-wave eigenmodes decreases. Therefore, the free surface has more pronounced effects at large Froude numbers and small spanwise wavenumbers.

For the streamwise-varying case ($\alpha h \ne 0$), the shear part of the flow field also consists of a pair of streamwise vortices and relatively weak streaks of streamwise velocity moving at a speed $c_s$, which is approximately the same as the projection of the surface base flow speed in the wavenumber direction. We define a new coordinate system $(\tilde {x},{\tilde {y}},\tilde {z})$ with its spanwise-axis $\tilde {z}$ along the wavenumber direction. In the plane (${\tilde {y}},{\tilde {z}}-c_st$), i.e. the plane moving with the streamwise vortices and streaks at a speed of $c_s$, the two surface-wave eigenmodes propagate in opposite directions along the $\tilde {z}$-axis at the same speed, and the spanwise location of the shear part remains fixed over time. Similar to the streamwise-uniform case, it is also proven that in the moving plane, a standing wave riding on the streamwise vortices can lead to the maximum energy growth rate, provided that the surface elevation of the standing wave is maximised at the initial time and the spanwise phase is the same as that of the shear part of the streamwise velocity.

Finally, we remark that although the present study reveals only a linear mechanism, our results are consistent with the observations from direct numerical simulations and laboratory experiments. In other canonical wall-bounded turbulence problems, it has been found that linear processes are highly important for sustaining turbulence. There exists a consensus in the research community that the linear lifting-up effect, leading to the non-modal transient growth of perturbation energy, plays an important role in the generation of very-large-scale streaks, and the secondary instability of the very-large-scale streaks induced by the lift-up mechanism is linked to the generation of LSMs. The present work and the work of Camporeale et al. (2021) also show these two processes in open channel flows. In the free-surface open channel flows, other possible nonlinear mechanisms may also be important for wave–turbulence interactions, which should be studied in a nonlinear framework in future works.