Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Graham, Michael D.
2014.
Drag reduction and the dynamics of turbulence in simple and complex fluids.
Physics of Fluids,
Vol. 26,
Issue. 10,
Park, Jae Sung
and
Graham, Michael D.
2015.
Exact coherent states and connections to turbulent dynamics in minimal channel flow.
Journal of Fluid Mechanics,
Vol. 782,
Issue. ,
p.
430.
Beaume, Cédric
Chini, Gregory P.
Julien, Keith
and
Knobloch, Edgar
2015.
Reduced description of exact coherent states in parallel shear flows.
Physical Review E,
Vol. 91,
Issue. 4,
Deguchi, Kengo
2015.
Self-sustained states at Kolmogorov microscale.
Journal of Fluid Mechanics,
Vol. 781,
Issue. ,
Jiménez, Javier
2015.
Direct detection of linearized bursts in turbulence.
Physics of Fluids,
Vol. 27,
Issue. 6,
Pralits, Jan O.
Bottaro, Alessandro
and
Cherubini, Stefania
2015.
Weakly nonlinear optimal perturbations.
Journal of Fluid Mechanics,
Vol. 785,
Issue. ,
p.
135.
Deguchi, Kengo
and
Hall, Philip
2015.
Asymptotic descriptions of oblique coherent structures in shear flows.
Journal of Fluid Mechanics,
Vol. 782,
Issue. ,
p.
356.
Beaume, Cédric
Knobloch, Edgar
Chini, Gregory P
and
Julien, Keith
2015.
Exact coherent structures in an asymptotically reduced description of parallel shear flows.
Fluid Dynamics Research,
Vol. 47,
Issue. 1,
p.
015504.
Gómez, F.
Blackburn, H. M.
Rudman, M.
Sharma, A. S.
and
McKeon, B. J.
2016.
Streamwise-varying steady transpiration control in turbulent pipe flow.
Journal of Fluid Mechanics,
Vol. 796,
Issue. ,
p.
588.
Deguchi, Kengo
and
Hall, Philip
2016.
On the instability of vortex–wave interaction states.
Journal of Fluid Mechanics,
Vol. 802,
Issue. ,
p.
634.
Ozcakir, Ozge
Tanveer, Saleh
Hall, Philip
and
Overman, Edward A.
2016.
Travelling wave states in pipe flow.
Journal of Fluid Mechanics,
Vol. 791,
Issue. ,
p.
284.
Sekimoto, Atsushi
and
Jiménez, Javier
2017.
Vertically localised equilibrium solutions in large-eddy simulations of homogeneous shear flow.
Journal of Fluid Mechanics,
Vol. 827,
Issue. ,
p.
225.
Chini, G. P.
Montemuro, B.
White, C. M.
and
Klewicki, J.
2017.
A self-sustaining process model of inertial layer dynamics in high Reynolds number turbulent wall flows.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 375,
Issue. 2089,
p.
20160090.
Kushwaha, Anubhav
Park, Jae Sung
and
Graham, Michael D.
2017.
Temporal and spatial intermittencies within channel flow turbulence near transition.
Physical Review Fluids,
Vol. 2,
Issue. 2,
Whalley, Richard D.
Park, Jae Sung
Kushwaha, Anubhav
Dennis, David J. C.
Graham, Michael D.
and
Poole, Robert J.
2017.
Low-drag events in transitional wall-bounded turbulence.
Physical Review Fluids,
Vol. 2,
Issue. 3,
Olvera, D.
and
Kerswell, R. R.
2017.
Exact coherent structures in stably stratified plane Couette flow.
Journal of Fluid Mechanics,
Vol. 826,
Issue. ,
p.
583.
Deguchi, Kengo
2017.
Scaling of small vortices in stably stratified shear flows.
Journal of Fluid Mechanics,
Vol. 821,
Issue. ,
p.
582.
Dessup, Tommy
Tuckerman, Laurette S.
Wesfreid, José Eduardo
Barkley, Dwight
and
Willis, Ashley P.
2018.
Self-sustaining process in Taylor-Couette flow.
Physical Review Fluids,
Vol. 3,
Issue. 12,
Yang, Qiang
Willis, Ashley P.
and
Hwang, Yongyun
2018.
Energy production and self-sustained turbulence at the Kolmogorov scale in Couette flow.
Journal of Fluid Mechanics,
Vol. 834,
Issue. ,
p.
531.
Park, Jae Sung
Shekar, Ashwin
and
Graham, Michael D.
2018.
Bursting and critical layer frequencies in minimal turbulent dynamics and connections to exact coherent states.
Physical Review Fluids,
Vol. 3,
Issue. 1,
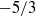 $- 5/ 3$ power of the wavenumber.
$- 5/ 3$ power of the wavenumber.