Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T08:31:04.681Z Has data issue: false hasContentIssue false
  • English
  • Français

Laboratory experiments on the temporal decay of homogeneous anisotropic turbulence

Published online by Cambridge University Press:  07 January 2019

L. B. Esteban Open the ORCID record for L. B. Esteban [Opens in a new window] ,
J. S. Shrimpton  and
B. Ganapathisubramani Open the ORCID record for B. Ganapathisubramani [Opens in a new window]
L. B. Esteban
Affiliation:
Aerodynamics and Flight Mechanics Group, University of Southampton, University Rd, Southampton SO17 1BJ, UK
J. S. Shrimpton
Affiliation:
Aerodynamics and Flight Mechanics Group, University of Southampton, University Rd, Southampton SO17 1BJ, UK
B. Ganapathisubramani*
Affiliation:
Aerodynamics and Flight Mechanics Group, University of Southampton, University Rd, Southampton SO17 1BJ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We experimentally investigate the temporal decay of homogeneous anisotropic turbulence, monitoring the evolution of velocity fluctuations, dissipation and turbulent length scales over time. We employ an apparatus in which two facing random jet arrays of water pumps generate turbulence with negligible mean flow and shear over a volume that is much larger than the initial characteristic turbulent large scale of the flow. The Reynolds number based on the Taylor microscale for forced turbulence is 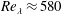$Re_{\unicode[STIX]{x1D706}}\approx 580$ and the axial-to-radial ratio of the root mean square velocity fluctuations is 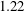$1.22$. Two velocity components are measured by particle image velocimetry at the symmetry plane of the water tank. Measurements are taken for both ‘stationary’ forced turbulence and natural decaying turbulence. For decaying turbulence, power-law fits to the decay of turbulent kinetic energy reveal two regions over time; in the near-field region (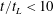$t/t_{L}<10$, 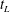$t_{L}$ is the integral time scale of the forced turbulence) a decay exponent 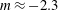$m\approx -2.3$ is found whereas for the far-field region (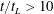$t/t_{L}>10$) the value of the decay exponent was found to be affected by turbulence saturation. The near-field exhibits features of non-equilibrium turbulence with constant 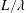$L/\unicode[STIX]{x1D706}$ and varying 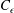$C_{\unicode[STIX]{x1D716}}$ (dissipation constant). We found a decay exponent 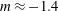$m\approx -1.4$ for the unsaturated regime and 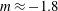$m\approx -1.8$ for the saturated regime, in good agreement with previous numerical and experimental studies. We also observe a fast evolution towards isotropy at small scales, whereas anisotropy at large scales remains in the flow over more than 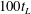$100t_{L}$. Direct estimates of dissipation are obtained and the decay exponent agrees well with the prediction 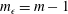$m_{\unicode[STIX]{x1D716}}=m-1$ throughout the decay process.

JFM classification

Turbulent Flows: Homogeneous turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 862 , 10 March 2019 , pp. 99 - 127
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. & Westerweel, J. 2011 Particle Image Velocimetry. Cambridge University Press.Google Scholar
Alvarado, A. P., Mydlarski, L. & Gaskin, S. 2016 Effect of the driving algorithm on the turbulence generated by a random jet array. Exp. Fluids 57, 20–32.Google Scholar
Antonia, R. A. & Orlandi, P. 2004 Similarity of decaying isotropic turbulence with a passive scalar. J. Fluid Mech. 505, 123–151.Google Scholar
Antonia, R. A., Satyaprakash, B. R. & Hussain, A. K. M. F. 1982 Statistics of fine-scale velocity in turbulent plane and circular jets. J. Fluid Mech. 119, 55–89.Google Scholar
Antonia, R. A., Tang, S. L., Djenidi, L. & Danaila, L. 2015 Boundedness of the velocity derivative skewness in various turbulent flows. J. Fluid Mech. 781, 727–744.Google Scholar
Batchelor, G. K. 1948 Decay of isotropic turbulence in the initial period. Proc. R. Soc. Lond. A 193, 539–558.Google Scholar
Bellani, G. & Variano, E. A. 2013 Homogeneity and isotropy in a laboratory turbulent flow. Exp. Fluids 55, 1646–1666.Google Scholar
Biferale, L., Boffetta, G., Celani, A., Lanotte, A., Toschi, F. & Vergassola, M. 2003 The decay of homonegeous anisotropic turbulence. Phys. Fluids 15, 2105–2112.Google Scholar
Blum, D. B., Bewley, G. P., Bodenschatz, E., Gibert, M., Gylfason, A., Mydlarski, L., Voth, G. A., Xu, H. & Yeung, P. K. 2011 Signatures of non-universal large scales in conditional structure functions from various turbulent flows. New J. Phys. 13, 113020.Google Scholar
Bodenschatz, E., Bewley, G. P., Nobach, H., Sinhuber, M. & Xu, H. 2014 Variable density turbulence tunnel facility. Rev. Sci. Instrum. 85, 331–368, 093908.Google Scholar
de Bruyn Kops, S. M. & Riley, J. J. 1998 Direct numerical simulation of laboratory experiments in isotropic turbulence. Phys. Fluids 10, 2125–2127.Google Scholar
Burattini, P., Lavoie, P., Agrawal, A., Djenidi, L. & Antonia, R. A. 2006 On the power law of decaying homogeneous isotropic turbulence at low Reynolds number. Phys. Rev. E 73, 066304.Google Scholar
Burattini, P., Lavoie, P. & Antonia, R. A. 2005 On the normalized turbulent energy dissipation rate. Phys. Fluids 17, 098103.Google Scholar
Burattini, P., Lavoie, P. & Antonia, R. A. 2008 Velocity derivative skewness in isotropic turbulence and its measurement with hot wires. Exp. Fluids 45, 523–535.Google Scholar
Buxton, O. R. H., Laizet, S. & Ganapathisubramani, B. 2011 Dissipation rate estimation from piv in zero-mean isotropic turbulence. Exp. Fluids 51, 1417–1437.Google Scholar
Carter, D., Petersen, A., Amili, O. & Coletti, F. 2016 Generating and controlling homogeneous air turbulence using random jet arrays. Exp. Fluids 57, 189.Google Scholar
Chang, K., Bewley, G. P. & Bodenschatz, E. 2012 Experimental study of the influence of anisotropy on the inertial scales of turbulence. J. Fluid Mech. 692, 464–481.Google Scholar
Compte-Bellot, G. & Corrsin, S. 1966 The use of a contraction to improve the isotropy of grid-generated turbulence. J. Fluid Mech. 62, 115–143.Google Scholar
De Silva, I. & Fernando, H. 1994 Oscillating grids as a source of nearly isotropic turbulence. Phys. Fluids 6, 2455–2464.Google Scholar
Delbos, S., Weitbrecht, V., Bleninger, T., Grand, P. P., Chassaing, E., Lincot, D., Kerrec, O. & Jirka, G. H. 2009 Homogeneous turbulence at an electrodeposition surface induced by randomly firing jet arrays. Exp. Fluids 46, 1105–1115.Google Scholar
Djenidi, L., Lefeuvre, N., Kamruzzaman, M. & Antonia, R. A. 2017 On the normalized dissipation parameter ce in decaying turbulence. J. Fluid Mech. 817, 61–79.Google Scholar
Dou, Z., Pecenak, Z. K., Cao, L., Woodward, S. H., Liang, Z. & Meng, H. 2016 Piv measurement of high-Reynolds-number homogeneous and isotropic turbulence in an enclosed flow apparatus with fan agitation. Meas. Sci. Technol. 27 (3), 035305.Google Scholar
Dryden, H. L. 1943 A review of the statistical theory of turbulence. Q. Appl. Maths 1, 7–42.Google Scholar
Elghobashi, S. 2019 Dns of turbulent flows laden with droplets or bubbles. Annu. Rev. Fluid Mech. 51, 1.Google Scholar
Esteban, L. B., Shrimpton, J. & Ganapathisubramani, B. 2018 Edge effects on the fluttering characteristics of freely falling planar particles. Phys. Rev. Fluids 3, 064302.Google Scholar
Esteban, L. B., Shrimpton, J. & Ganapathisubramani, B. 2019 Study of the circularity effect on drag of disk-like particles. Intl J. Multiphase Flow 110, 189–197.Google Scholar
Ganapathisubramani, B., Lakshminarasimhan, K. & Clemens, T. 2007 Determination of complete velocity gradient tensor by using cinematographic stereoscopic piv in a turbulent jet. Exp. Fluids 42, 923–939.Google Scholar
George, W. K. & Hussein, H. J. 1991 Locally axisymmetric turbulence. J. Fluid Mech. 223, 1–23.Google Scholar
Goepfert, C., Marie, J. L., Chareyron, D. & Lance, M. 2010 Characterization fo a system generating a homogeneous isotropic turbulence field by free synthetic jets. Exp. Fluids 48, 809–822.Google Scholar
Goto, S. & Vassilicos, J. C. 2016 Unsteady turbulence cascades. Phys. Rev. E 94, 053108.Google Scholar
el Hak, M. G. & Corrsin, S. 1974 Measurements of the nearly isotropic turbulence behind a uniform jet grid. J. Fluid Mech. 62, 115–143.Google Scholar
Hearst, R. J. & Lavoie, P. 2014 Decay of turbulence generated by a square-fractal-element grid. J. Fluid Mech. 741, 567–584.Google Scholar
Hellström, L. H. O., Zlatinov, M. B., Cao, G. & Smits, A. J. 2013 Turbulent pipe flow downstream of a 90 bend. J. Fluid Mech. 735, R7.Google Scholar
Huang, M. J. & Leonard, A. 1994 Power-law decay of homogeneous turbulence at low Reynolds numbers. Phys. Fluids 6, 3765–3775.Google Scholar
Hurst, D. J. & Vassilicos, J. C. 2007 Scalings and decay of fractal-generated turbulence. Phys. Fluids 19, 035103.Google Scholar
Hwang, W. & Eaton, J. K. 2004 Creating homogeneous and isotropic turbulence without a mean flow. Exp. Fluids 36, 444–454.Google Scholar
de Jong, J., Cao, L., Woodward, S. H., Salazar, J. P. L. C., Collins, L. R. & Meng, H. 2009 Dissipation rate estimation from piv in zero-mean isotropic turbulence. Exp. Fluids 46, 499–515.Google Scholar
Kang, H. S., Chester, S. & Meneveau, C. 2003 Decaying turbulence in an active-grid-generated flow and comparisons with large-eddy simulation. J. Fluid Mech. 480, 129–160.Google Scholar
Khorsandi, B., Gaskin, S. & Mydlarski, L. 2013 Effect of backgroud turbulence on an axisymmetric turbulent jet. J. Fluid Mech. 736, 250–286.Google Scholar
Kistler, A. L. & Vrebalovich, T. 1966 Grit turbulence at large Reynolds numbers. J. Fluid Mech. 26, 37–47.Google Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds. C. R. Acad. Sci. URSS 30, 301.Google Scholar
Korneyev, A. I. & Sedov, L. I. 1976 Theory of isotropic turbulence and its comparison with experimental data. Fluid Mech. Soc. Res. 5, 37–48.Google Scholar
Krogstad, P. A. & Davidson, P. A. 2011 Freely decaying, homogeneous turbulence generated by multi-scale grids. J. Fluid Mech. 680, 417–434.Google Scholar
Larssen, J. V. & Devenport, W. J. 2011 On the generation of large-scale homogeneous turbulence. Exp. Fluids 50, 1207–1223.Google Scholar
Lavertu, T. M., Mydlarski, L. & Gaskin, S. J. 2006 Differential diffusion of high-schmidt-number passive scalars in a turbulent jet. J. Fluid Mech. 612, 439–475.Google Scholar
Lavoie, P., Djenidi, L. & Antonia, R. A. 2007 Effects of initial conditions in decaying turbulence generated by passive grids. J. Fluid Mech. 585, 395–420.Google Scholar
Ling, S. C. & Wang, C. A. 1972 Decay of isotropic turbulence generated by a mechanically agitated grid. Phys. Fluids 15, 1363–1369.Google Scholar
Lu, J., Fugal, J. P., Nordsiek, H., Saw, E. W., Shaw, R. A. & Yang, W. 2008 Lagrangian particle tracking in three dimensions via single-camera in-line digital holography. New J. Phys. 10, 125013.Google Scholar
Makita, H. 1991 Realization of a large-scale turbulence field in a small wind tunnel. Fluid Dyn. Res. 8, 53–64.Google Scholar
Marie, L. & Daviaud, F. 2004 Experimental measurement of the scale-by-scale momentum transport budget in a turbulent shear flow. Phys. Fluids 16, 457–461.Google Scholar
Mazellier, N. & Vassilicos, J. C. 2010 Turbulence without Richardson-Kolmogorov cascade. Phys. Fluids 22, 075101.Google Scholar
McDougall, T. J. 1979 Measurements of turbulence in a zero-mean shear mixed layer. J. Fluid Mech. 94, 409–431.Google Scholar
McKenna, S. P. & McGillis, W. R. 2004 Observations of flow repeatability and secondary circulation in an oscillating grid-stirred tank. Phys. Fluids 16, 3499–3502.Google Scholar
Meldi, M. 2016 The signature of initial production mechanisms in isotropic turbulence decay. Phys. Fluids 28, 035105.Google Scholar
Meldi, M., Lejemble, H. & Sagaut, P. 2014 On the emergence of non-classical decay regimes in multiscale/fractal generated isotropic turbulence. J. Fluid Mech. 756, 816–843.Google Scholar
Meldi, M. & Sagaut, P. 2014 On non-self-similar regimes in homogeneous isotropic turbulence decay. J. Fluid Mech. 711, 364–393.Google Scholar
Meldi, M. & Sagaut, P. 2017 Turbulence in a box: quantification of large-scale resolution effects in isotropic turbulence free decay. J. Fluid Mech. 818, 697–715.Google Scholar
Meldi, M., Sagaut, P. & Lucor, D. 2011 A stochastic view of isotropic turbulence decay. J. Fluid Mech. 668, 351–362.Google Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.Google Scholar
Mydlarski, L. & Warhaft, Z. 1998 Passive scalar statistics in high-Peclet-number grid turbulence. J. Fluid Mech. 358, 135–175.Google Scholar
Perot, J. B. 2011 Determination of the decay exponent in mechanically stirred isotropic turbulence. AIP Advances 1, 022104.Google Scholar
Saarenrinne, P. & Piirto, M. 2000 Turbulent kinetic energy dissipation rate estimation from piv velocity vector fields. Exp. Fluids 29, 300–307.Google Scholar
Skrbek, L. & Stalp, S. R. 2000 On the decay of homogeneous isotropic turbulence. Phys. Rev. Lett. 12, 1997–2019.Google Scholar
Sreenivasan, K. R. 1984 On the scaling of the energy dissipation rate. Phys. Fluids 27, 1048.Google Scholar
Sreenivasan, K. R. 1995 On the universality of the Kolmogorov constant. Phys. Fluids 7, 2778–2784.Google Scholar
Sreenivasan, K. R. 1998 An update on the energy dissipation rate in isotropic turbulence. Phys. Fluids 10, 528–529.Google Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.Google Scholar
Tanaka, T. & Eaton, J. K. 2007 A correction method for measuring turbulence kinetic energy dissipation rate by piv. Exp. Fluids 42, 893–902.Google Scholar
Taylor, G. I. 1935 Statistical theory of turbulence. Proc. R. Soc. Lond. A 151, 421–444.Google Scholar
Taylor, G. I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. A 164, 421–444.Google Scholar
Touil, H., Bertoglio, J. P. & Shao, L. 2002 The decay of turbulence in a bounded domain. J. Turbul. 3, 049.Google Scholar
Uberoi, M. S. & Wallis, S. 1967 Effect of grid geometry on turbulence decay. Phys. Fluids 10, 1216–1224.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2011 The decay of turbulence generated by a class of multiscale grids. J. Fluid Mech. 687, 300–340.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2012 Dependence of decaying homogeneous isotropic turbulence on inflow conditions. Phys. Lett. A 376, 510–514.Google Scholar
Variano, E. A., Bodenschatz, E. & Cowen, E. A. 2004 A random synthetic jet array driven turbulence tank. Exp. Fluids 37, 613–615.Google Scholar
Variano, E. A. & Cowen, E. A. 2008 A random-jet-stirred turbulence tank. J. Fluid Mech. 604, 1–32.Google Scholar
Vassilicos, J. C. 2015 Dissipation in turbulent flows. Annu. Rev. Fluid Mech. 47, 95–114.Google Scholar
Volk, R., Odier, P. & Pinton, J. F. 2006 Fluctuation of magnetic induction in von Karman swirling flows. Phys. Fluids 18, 085105.Google Scholar
Von Karman, T. & Howarth, L. 1938 On the statistical theory of isotropic turbulence. Proc. R. Soc. Lond. A 164, 192–215.Google Scholar
Warnaars, T. A., Hondzo, M. & Carper, M. A. 2006 A desktop apparatus for studying interactions between microorganisms and small-scale fluid motion. Hydrobiologia 563, 431–443.Google Scholar
Webster, D. R., Brathwaite, A. & Yen, J. 2004 A novel laboratory apparatus for simulating isotropic oceanic turbulence at low Reynolds number. Limnol. Oceanogr. 2, 1–12.Google Scholar
Wray, A.1998 Decaying isotropic turbulence. Tech. Rep. AGARD Advisory Rep.Google Scholar
Zimmermann, R., Xu, H., Gasteuil, Y., Bourgoin, M., Volk, R., Pinton, J. F. & Bodenschatz, E. 2010 The lagrangian exploration module: an apparatus for the study of statistically homogeneous and isotropic turbulence. Rev. Sci. Instrum. 81, 055112.Google Scholar