Published online by Cambridge University Press: 19 August 2019
Starting from coupled Boltzmann–Enskog (BE) kinetic equations for a two-particle system consisting of hard spheres, a hyperbolic two-fluid model for binary, hard-sphere mixtures is derived with separate mean velocities and energies for each phase. In addition to spatial transport, the BE kinetic equations account for particle–particle collisions, using an elastic hard-sphere collision model, and the Archimedes (buoyancy) force due to spatial gradients of the pressure in each phase, as well as other forces involving spatial gradients (e.g. lift). In the derivation, the particles in a given phase have identical mass and volume, and have no internal degrees of freedom (i.e. the particles are adiabatic). The ‘hard-sphere-fluid’ phase is obtained in the limit where the particle diameter in one phase tends to zero with fixed phase density so that the number of fluid particles tends to infinity. The moment system resulting from the two BE kinetic equations is closed at second order by invoking the anisotropic Gaussian closure. The resulting two-fluid model for a binary, hard-sphere mixture therefore consists (for each phase 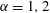 $\unicode[STIX]{x1D6FC}=1,2$) of transport equations for the mass
$\unicode[STIX]{x1D6FC}=1,2$) of transport equations for the mass 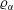 $\unicode[STIX]{x1D71A}_{\unicode[STIX]{x1D6FC}}$, mean momentum
$\unicode[STIX]{x1D71A}_{\unicode[STIX]{x1D6FC}}$, mean momentum 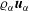 $\unicode[STIX]{x1D71A}_{\unicode[STIX]{x1D6FC}}\boldsymbol{u}_{\unicode[STIX]{x1D6FC}}$ (where
$\unicode[STIX]{x1D71A}_{\unicode[STIX]{x1D6FC}}\boldsymbol{u}_{\unicode[STIX]{x1D6FC}}$ (where 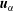 $\boldsymbol{u}_{\unicode[STIX]{x1D6FC}}$ is the velocity) and a symmetric, second-order, kinetic energy tensor
$\boldsymbol{u}_{\unicode[STIX]{x1D6FC}}$ is the velocity) and a symmetric, second-order, kinetic energy tensor 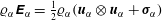 $\unicode[STIX]{x1D71A}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D640}_{\unicode[STIX]{x1D6FC}}=\frac{1}{2}\unicode[STIX]{x1D71A}_{\unicode[STIX]{x1D6FC}}(\boldsymbol{u}_{\unicode[STIX]{x1D6FC}}\otimes \boldsymbol{u}_{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D748}_{\unicode[STIX]{x1D6FC}})$. The trace of the fluctuating energy tensor
$\unicode[STIX]{x1D71A}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D640}_{\unicode[STIX]{x1D6FC}}=\frac{1}{2}\unicode[STIX]{x1D71A}_{\unicode[STIX]{x1D6FC}}(\boldsymbol{u}_{\unicode[STIX]{x1D6FC}}\otimes \boldsymbol{u}_{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D748}_{\unicode[STIX]{x1D6FC}})$. The trace of the fluctuating energy tensor 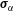 $\unicode[STIX]{x1D748}_{\unicode[STIX]{x1D6FC}}$ is
$\unicode[STIX]{x1D748}_{\unicode[STIX]{x1D6FC}}$ is 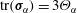 $\text{tr}(\unicode[STIX]{x1D748}_{\unicode[STIX]{x1D6FC}})=3\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6FC}}$ where
$\text{tr}(\unicode[STIX]{x1D748}_{\unicode[STIX]{x1D6FC}})=3\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6FC}}$ where 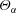 $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6FC}}$ is the phase temperature (or granular temperature). Thus,
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D6FC}}$ is the phase temperature (or granular temperature). Thus, 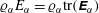 $\unicode[STIX]{x1D71A}_{\unicode[STIX]{x1D6FC}}E_{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D71A}_{\unicode[STIX]{x1D6FC}}\text{tr}(\unicode[STIX]{x1D640}_{\unicode[STIX]{x1D6FC}})$ is the total kinetic energy, the sum over
$\unicode[STIX]{x1D71A}_{\unicode[STIX]{x1D6FC}}E_{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D71A}_{\unicode[STIX]{x1D6FC}}\text{tr}(\unicode[STIX]{x1D640}_{\unicode[STIX]{x1D6FC}})$ is the total kinetic energy, the sum over  $\unicode[STIX]{x1D6FC}$ of which is the total kinetic energy of the system, a conserved quantity. From the analysis, it is found that the BE finite-size correction leads to exact phase pressure (or stress) tensors that depend on the mean-slip velocity
$\unicode[STIX]{x1D6FC}$ of which is the total kinetic energy of the system, a conserved quantity. From the analysis, it is found that the BE finite-size correction leads to exact phase pressure (or stress) tensors that depend on the mean-slip velocity 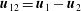 $\boldsymbol{u}_{12}=\boldsymbol{u}_{1}-\boldsymbol{u}_{2}$, as well as the phase temperatures for both phases. These pressure tensors also appear in the momentum-exchange terms in the mean momentum equations that produce the Archimedes force, as well as drag contributions due to fluid compressibility and a lift force due to mean fluid-velocity gradients. The closed BE energy flux tensors show a similar dependence on the mean-slip velocity. The characteristic polynomial of the flux matrix from the one-dimensional model is computed symbolically and depends on five parameters: the particle volume fractions
$\boldsymbol{u}_{12}=\boldsymbol{u}_{1}-\boldsymbol{u}_{2}$, as well as the phase temperatures for both phases. These pressure tensors also appear in the momentum-exchange terms in the mean momentum equations that produce the Archimedes force, as well as drag contributions due to fluid compressibility and a lift force due to mean fluid-velocity gradients. The closed BE energy flux tensors show a similar dependence on the mean-slip velocity. The characteristic polynomial of the flux matrix from the one-dimensional model is computed symbolically and depends on five parameters: the particle volume fractions 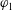 $\unicode[STIX]{x1D711}_{1}$,
$\unicode[STIX]{x1D711}_{1}$, 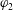 $\unicode[STIX]{x1D711}_{2}$, the phase density ratio
$\unicode[STIX]{x1D711}_{2}$, the phase density ratio 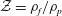 ${\mathcal{Z}}=\unicode[STIX]{x1D70C}_{f}/\unicode[STIX]{x1D70C}_{p}$, the phase temperature ratio
${\mathcal{Z}}=\unicode[STIX]{x1D70C}_{f}/\unicode[STIX]{x1D70C}_{p}$, the phase temperature ratio 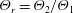 $\unicode[STIX]{x1D6E9}_{r}=\unicode[STIX]{x1D6E9}_{2}/\unicode[STIX]{x1D6E9}_{1}$ and the mean-slip Mach number
$\unicode[STIX]{x1D6E9}_{r}=\unicode[STIX]{x1D6E9}_{2}/\unicode[STIX]{x1D6E9}_{1}$ and the mean-slip Mach number 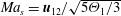 $Ma_{s}=\boldsymbol{u}_{12}/\sqrt{5\unicode[STIX]{x1D6E9}_{1}/3}$. By applying Sturm’s Theorem to the characteristic polynomial, it is demonstrated that the model is hyperbolic over a wide range of these parameters, in particular, for the physically most relevant values.
$Ma_{s}=\boldsymbol{u}_{12}/\sqrt{5\unicode[STIX]{x1D6E9}_{1}/3}$. By applying Sturm’s Theorem to the characteristic polynomial, it is demonstrated that the model is hyperbolic over a wide range of these parameters, in particular, for the physically most relevant values.