Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-01T11:47:31.847Z Has data issue: false hasContentIssue false
  • English
  • Français

Irreversible mixing by unstable periodic orbits in buoyancy dominated stratified turbulence

Published online by Cambridge University Press:  26 October 2017

Dan Lucas Open the ORCID record for Dan Lucas [Opens in a new window]  and
C. P. Caulfield Open the ORCID record for C. P. Caulfield [Opens in a new window]
Dan Lucas*
Affiliation:
School of Computing and Mathematics, Keele University, Staffordshire, ST5 5BG
C. P. Caulfield
Affiliation:
BP Institute, University of Cambridge, Madingley Rise, Madingley Road, Cambridge CB3 0EZ, UK Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider turbulence driven by a large-scale horizontal shear in Kolmogorov flow (i.e. with sinusoidal body forcing) and a background linear stable stratification with buoyancy frequency 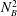$N_{B}^{2}$ imposed in the third, vertical direction in a fluid with kinematic viscosity $\unicode[STIX]{x1D708}$. This flow is known to be organised into layers by nonlinear unstable steady states, which incline the background shear in the vertical and can be demonstrated to be the finite-amplitude saturation of a sequence of instabilities, originally from the laminar state. Here, we investigate the next order of motions in this system, i.e. the time-dependent mechanisms by which the density field is irreversibly mixed. This investigation is achieved using ‘recurrent flow analysis’. We identify (unstable) periodic orbits, which are embedded in the turbulent attractor, and use these orbits as proxies for the chaotic flow. We find that the time average of an appropriate measure of the ‘mixing efficiency’ of the flow 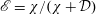$\mathscr{E}=\unicode[STIX]{x1D712}/(\unicode[STIX]{x1D712}+{\mathcal{D}})$ (where 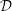${\mathcal{D}}$ is the volume-averaged kinetic energy dissipation rate and 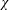$\unicode[STIX]{x1D712}$ is the volume-averaged density variance dissipation rate) varies non-monotonically with the time-averaged buoyancy Reynolds numbers 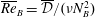$\overline{Re}_{B}=\overline{{\mathcal{D}}}/(\unicode[STIX]{x1D708}N_{B}^{2})$, and is bounded above by $1/6$, consistently with the classical model of Osborn (J. Phys. Oceanogr., vol. 10 (1), 1980, pp. 83–89). There are qualitatively different physical properties between the unstable orbits that have lower irreversible mixing efficiency at low 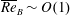$\overline{Re}_{B}\sim O(1)$ and those with nearly optimal 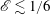$\mathscr{E}\lesssim 1/6$ at intermediate 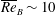$\overline{Re}_{B}\sim 10$. The weaker orbits, inevitably embedded in more strongly stratified flow, are characterised by straining or ‘scouring’ motions, while the more efficient orbits have clear overturning dynamics in more weakly stratified, and apparently shear-unstable flow.

JFM classification

Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Turbulent Flows: Stratified turbulence Mixing: Turbulent mixing
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 832 , 10 December 2017 , R1
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ashurst, Wm. T., Kerstein, A. R., Kerr, R. M. & Gibson, C. H. 1987 Alignment of vorticity and scalar gradient with strain rate in simulated Navier–Stokes turbulence. Phys. Fluids 30 (8), 2343–2353.Google Scholar
Chandler, G. J. & Kerswell, R. R. 2013 Invariant recurrent solutions embedded in a turbulent two-dimensional Kolmogorov flow. J. Fluid Mech. 722, 554–595.CrossRefGoogle Scholar
Cvitanović, P. & Gibson, J. F. 2010 Geometry of the turbulence in wall-bounded shear flows: periodic orbits. Phys. Scr. 142, 014007.Google Scholar
Garaud, P., Gallet, B. & Bischoff, T. 2015 The stability of stratified spatially periodic shear flows at low Péclet number. Phys. Fluids 27 (8), 084104.Google Scholar
Ivey, G. N., Winters, K. B. & Koseff, J. R. 2008 Density stratification, turbulence, but how much mixing? Annu. Rev. Fluid Mech. 40, 169–184.Google Scholar
Kawahara, G. & Kida, S. 2001 Periodic motion embedded in plane Couette turbulence: regeneration cycle and burst. J. Fluid Mech. 449, 291.CrossRefGoogle Scholar
Kawahara, G., Uhlmann, M. & van Veen, L. 2012 The significance of simple invariant solutions in turbulent flows. Annu. Rev. Fluid Mech. 44 (1), 203–225.Google Scholar
Linden, P. F. 1979 Mixing in stratified fluids. Geophys. Astrophys. Fluid Dyn. 13 (1), 3–23.CrossRefGoogle Scholar
Lucas, D., Caulfield, C. P. & Kerswell, R. R. 2017 Layer formation in horizontally forced stratified turbulence: connecting exact coherent structures to linear instabilities. J. Fluid Mech. 832, 409–437.Google Scholar
Lucas, D. & Kerswell, R. R. 2015 Recurrent flow analysis in spatiotemporally chaotic 2-dimensional Kolmogorov flow. Phys. Fluids 27 (4), 045106.Google Scholar
Lucas, D. & Kerswell, R. R. 2017 Sustaining processes from recurrent flows in body-forced turbulence. J. Fluid Mech. 817, R3–11.Google Scholar
Maffioli, A., Brethouwer, G. & Lindborg, E. 2016 Mixing efficiency in stratified turbulence. J. Fluid Mech. 794, R3.CrossRefGoogle Scholar
Mashayek, A., Salehipour, H., Bouffard, D., Caulfield, C. P., Ferrari, R., Nikurashin, M., Peltier, W. R. & Smyth, W. D. 2017 Efficiency of turbulent mixing in the abyssal ocean circulation. Geophys. Res. Lett. 44 (12), 6296–6306.CrossRefGoogle Scholar
Mater, B. D. & Venayagamoorthy, S. K. 2014 The quest for an unambiguous parameterization of mixing efficiency in stably stratified geophysical flows. Geophys. Res. Lett. 41 (13), 4646–4653.Google Scholar
Osborn, T. R. 1980 Estimates of the local rate of vertical diffusion from dissipation measurements. J. Phys. Oceanogr. 10 (1), 83–89.Google Scholar
Peltier, W. R. & Caulfield, C. P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35, 135–167.Google Scholar
Salehipour, H. & Peltier, W. R. 2015 Diapycnal diffusivity, turbulent Prandtl number and mixing efficiency in Boussinesq stratified turbulence. J. Fluid Mech. 775, 464–500.CrossRefGoogle Scholar
Salehipour, H., Peltier, W. R., Whalen, C. B. & MacKinnon, J. A. 2016 A new characterization of the turbulent diapycnal diffusivities of mass and momentum in the ocean. Geophys. Res. Lett. 43 (7), 3370–3379.Google Scholar
Scotti, A. & White, B. 2016 The mixing efficiency of stratified turbulent boundary layers. J. Phys. Oceanogr. 46 (10), 3181–3191.CrossRefGoogle Scholar
Shih, L. H., Koseff, J. R., Ivey, G. N. & Ferziger, J. H. 2005 Parameterization of turbulent fluxes and scales using homogeneous sheared stably stratified turbulence simulations. J. Fluid Mech. 525, 193–214.Google Scholar
Smyth, W. D. 1999 Dissipation-range geometry and scalar spectra in sheared stratified turbulence. J. Fluid Mech. 401, 209–242.Google Scholar
van Veen, L., Kida, S. & Kawahara, G. 2006 Periodic motion representing isotropic turbulence. Fluid Dyn. Res. 38 (1), 19–46.CrossRefGoogle Scholar
Woods, A. W., Caulfield, C. P., Landel, J. R. & Kuesters, A. 2010 Non-invasive turbulent mixing across a density interface in a turbulent Taylor–Couette flow. J. Fluid Mech. 663, 347–357.Google Scholar
Zhou, Q., Taylor, J. R. & Caulfield, C. P. 2017 Self-similar mixing in stratified plane Couette flow for varying Prandtl number. J. Fluid Mech. 820, 86–120.Google Scholar

Lucas supplementary movie 1

Movie showing the streamwise velocity, u, for the unstable periodic orbit UPOo1. Time steps are 0.5 time units. Note animation is made in the frame travelling with the relative periodic orbit in order to visualise the periodicity in time.

Download Lucas supplementary movie 1(Video)
Video 3.2 MB

Lucas supplementary movie 2

Movie showing the total density, ρtot=ρ-z, for the unstable periodic orbit UPOo1. Time steps are 0.5 time units. Note animation is made in the frame travelling with the relative periodic orbit in order to visualise the periodicity in time.

Download Lucas supplementary movie 2(Video)
Video 2.7 MB

Lucas supplementary movie 3

Movie showing the streamwise velocity, u, for the unstable periodic orbit UPOl1. Time steps are 0.5 time units. Note animation is made in the frame travelling with the relative periodic orbit in order to visualise the periodicity in time.

Download Lucas supplementary movie 3(Video)
Video 5.4 MB

Lucas supplementary movie 4

Movie showing the total density, ρtot=ρ-z, for the unstable periodic orbit UPOl1. Time steps are 0.5 time units. Note animation is made in the frame travelling with the relative periodic orbit in order to visualise the periodicity in time.

Download Lucas supplementary movie 4(Video)
Video 4.7 MB

Lucas supplementary movie 5

Movie showing the perturbation density, ρ, for the unstable periodic orbit UPOl1. Time steps are 0.5 time units. Note animation is made in the frame travelling with the relative periodic orbit in order to visualise the periodicity in time.

Download Lucas supplementary movie 5(Video)
Video 6.7 MB