Article contents
Irregular self-similar configurations of shock-wave impingement on shear layers
Published online by Cambridge University Press: 14 June 2019
Abstract
An oblique shock impinging on a shear layer that separates two uniform supersonic streams, of Mach numbers 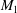 $M_{1}$ and
$M_{1}$ and 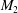 $M_{2}$, at an incident angle
$M_{2}$, at an incident angle 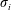 $\unicode[STIX]{x1D70E}_{i}$ can produce regular and irregular interactions with the interface. The region of existence of regular shock refractions with stable flow structures is delineated in the parametric space
$\unicode[STIX]{x1D70E}_{i}$ can produce regular and irregular interactions with the interface. The region of existence of regular shock refractions with stable flow structures is delineated in the parametric space 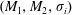 $(M_{1},M_{2},\unicode[STIX]{x1D70E}_{i})$ considering oblique-shock impingement on a supersonic vortex sheet of infinitesimal thickness. It is found that under supercritical conditions, the oblique shock fails to deflect both streams consistently and to provide balanced flow properties downstream. In this circumstance, the flow renders irregular configurations which, in the absence of characteristic length scales, exhibit self-similar pseudosteady behaviours. These cases involve shocks moving upstream at constant speed and increasing their intensity to comply with equilibrium requirements. Differences in the variation of propagation speed among the flows yield pseudosteady configurations that grow linearly with time. Supercritical conditions are described theoretically and reproduced numerically using highly resolved inviscid simulation.
$(M_{1},M_{2},\unicode[STIX]{x1D70E}_{i})$ considering oblique-shock impingement on a supersonic vortex sheet of infinitesimal thickness. It is found that under supercritical conditions, the oblique shock fails to deflect both streams consistently and to provide balanced flow properties downstream. In this circumstance, the flow renders irregular configurations which, in the absence of characteristic length scales, exhibit self-similar pseudosteady behaviours. These cases involve shocks moving upstream at constant speed and increasing their intensity to comply with equilibrium requirements. Differences in the variation of propagation speed among the flows yield pseudosteady configurations that grow linearly with time. Supercritical conditions are described theoretically and reproduced numerically using highly resolved inviscid simulation.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 10
- Cited by


