1. Introduction
Although the theory of inviscid liquid jets has a long history, much of the literature has concerned steady flows, often driven by gravity. However, there are many papers concerning unsteady jets, see for example Longuet-Higgins (Reference Longuet-Higgins1972) and Longuet-Higgins (Reference Longuet-Higgins1975) and, more recently, jets caused by the impact of a solid on an initially planar interface (King & Needham Reference King and Needham1994; Needham, Billingham & King Reference Needham, Billingham and King2007; Iafrati & Korobkin Reference Iafrati and Korobkin2008). When the solid is flat, very high-speed jets can be created at the corner of the impactor but only very recently has it been shown that such jets can occur spontaneously at a free surface and this is the phenomenon that has driven the research described in this paper.
The computations of Scolan (Reference Scolan2023) and Scolan & Etienne (Reference Scolan and Etienne2021) have revealed the onset of localised high-speed so-called ‘critical’ jets on the underside of breaking gravity waves, the time scale of the jet evolution being much shorter than that of the gravity wave. Their computations revealed the local evolution of the fluid velocity and pressure in some detail and, in particular, the existence of a pressure maximum in close proximity to the free surface, which produces local pressure gradients which are two orders of magnitude greater than the average value. The dramatic effects of such pressure maxima are apparent in shaped charges and in the free boundary configuration considered in Cooker (Reference Cooker2002).
Our aim in this paper is to describe a simple model for critical jet initiation in two-dimensional and axisymmetric flow, neglecting gravity effects. We suppose that, for time ![]() $t<0$, the liquid flow is that of a stagnation point at the origin created by remote dipoles at equal distances
$t<0$, the liquid flow is that of a stagnation point at the origin created by remote dipoles at equal distances ![]() $d$ above and below the stagnation point, as illustrated in figure 1. Such configurations are common in, say, the study of water entry problems, because the resulting velocity field tends to zero at infinity.
$d$ above and below the stagnation point, as illustrated in figure 1. Such configurations are common in, say, the study of water entry problems, because the resulting velocity field tends to zero at infinity.

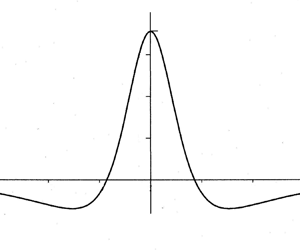
Figure 1. The initial streamlines for ![]() $y\leq 1$ when
$y\leq 1$ when ![]() $d=2$.
$d=2$.
With ![]() $d>1$, we now generate a free-boundary problem by instantaneously removing all the liquid above the line
$d>1$, we now generate a free-boundary problem by instantaneously removing all the liquid above the line ![]() $y=1$ at time
$y=1$ at time ![]() $t=0$ and assume that for
$t=0$ and assume that for ![]() $t>0$ the remaining liquid is exposed to a vacuum. Even for this configuration, there do not seem to be any exact solutions for finite values of
$t>0$ the remaining liquid is exposed to a vacuum. Even for this configuration, there do not seem to be any exact solutions for finite values of ![]() $d$. However, when
$d$. However, when ![]() $d$ is large, and also when
$d$ is large, and also when ![]() $d-1$ is small, the evolution of the jet can be revealed by asymptotic analysis, at least for certain times. The configuration is probably physically unrealistic but it models the pressure maximum and is susceptible to asymptotic analysis, as will be seen in §§ 2 and 3. Moreover, the pressure is not initially zero on
$d-1$ is small, the evolution of the jet can be revealed by asymptotic analysis, at least for certain times. The configuration is probably physically unrealistic but it models the pressure maximum and is susceptible to asymptotic analysis, as will be seen in §§ 2 and 3. Moreover, the pressure is not initially zero on ![]() $y=1$ as it is in Scolan (Reference Scolan2023) and Scolan & Etienne (Reference Scolan and Etienne2021). Nonetheless, it is hoped that our explicit asymptotic solutions will provide useful validation of numerical predictions of rapid jet formation.
$y=1$ as it is in Scolan (Reference Scolan2023) and Scolan & Etienne (Reference Scolan and Etienne2021). Nonetheless, it is hoped that our explicit asymptotic solutions will provide useful validation of numerical predictions of rapid jet formation.
In § 2, we will first consider the two-dimensional problem when ![]() $d\rightarrow \infty$ and we show that the boundary moves to infinity in finite time, henceforth referred to as blow-up. When the dipole is present, small-time solutions are presented that show how a jet begins to evolve, and asymptotic results are then obtained, first for large values of
$d\rightarrow \infty$ and we show that the boundary moves to infinity in finite time, henceforth referred to as blow-up. When the dipole is present, small-time solutions are presented that show how a jet begins to evolve, and asymptotic results are then obtained, first for large values of ![]() $d$ and, briefly, for small values of
$d$ and, briefly, for small values of ![]() $(d-1)$. Then we repeat this analysis for the axisymmetric version of the problem.
$(d-1)$. Then we repeat this analysis for the axisymmetric version of the problem.
2. The two-dimensional problem
The sudden jump in pressure at ![]() $t=0$ will cause a jump in acceleration in the liquid, which will then flow according to the following normalised model for the potential
$t=0$ will cause a jump in acceleration in the liquid, which will then flow according to the following normalised model for the potential ![]() $\phi (x,y,t)$ and the free surface
$\phi (x,y,t)$ and the free surface ![]() $y=f(x,t)$, assumed single valued. Also,
$y=f(x,t)$, assumed single valued. Also, ![]() $\phi$ and its first spatial derivatives will be continuous at
$\phi$ and its first spatial derivatives will be continuous at ![]() $t=0$. Then, for
$t=0$. Then, for ![]() $t>0$,
$t>0$,
where, on ![]() $y=f(x,t)$, the dynamic boundary condition for the pressure p is
$y=f(x,t)$, the dynamic boundary condition for the pressure p is
and we have taken the pressure to be zero at infinity when ![]() $d$ is finite. The kinematic boundary condition on
$d$ is finite. The kinematic boundary condition on ![]() $y=f(x,t)$ is
$y=f(x,t)$ is
Also ![]() $\phi$ has a suitably normalised dipole singularity at
$\phi$ has a suitably normalised dipole singularity at ![]() $(0,-d)$ and the initial conditions are
$(0,-d)$ and the initial conditions are
for ![]() $y\leq 1$ and
$y\leq 1$ and
2.1. Solutions for large  $d$
$d$
When we formally set ![]() $d = \infty$, then (2.4) becomes
$d = \infty$, then (2.4) becomes ![]() $\phi (x,y,0)= y^2-x^2$ and we can write
$\phi (x,y,0)= y^2-x^2$ and we can write
where ![]() $A(0)=1, B(0)=0$ and
$A(0)=1, B(0)=0$ and ![]() $F(0)=1$. Thus, from (2.2) and (2.3),
$F(0)=1$. Thus, from (2.2) and (2.3),
and we find that ![]() $A=F={1}/({1-2t}), B=-{2}/({3(1-2t)^3})+\tfrac {2}{3}$, which is one case of the family of explicit solutions described by Longuet-Higgins (Reference Longuet-Higgins1972). The pressure
$A=F={1}/({1-2t}), B=-{2}/({3(1-2t)^3})+\tfrac {2}{3}$, which is one case of the family of explicit solutions described by Longuet-Higgins (Reference Longuet-Higgins1972). The pressure ![]() $p$ is given by
$p$ is given by
having jumped from ![]() $-2(x^2 + y^2)$ to
$-2(x^2 + y^2)$ to ![]() $4(1-y^2)$ at
$4(1-y^2)$ at ![]() $t=0$. Thus, not only does blow-up occur when
$t=0$. Thus, not only does blow-up occur when ![]() $t=\tfrac {1}{2}$ but the pressure has a maximum that increases with time on the whole
$t=\tfrac {1}{2}$ but the pressure has a maximum that increases with time on the whole ![]() $x$-axis. We also note that when the stagnation-point flow is reversed so that
$x$-axis. We also note that when the stagnation-point flow is reversed so that ![]() $A(0)=-1$, the pressure still has a maximum on
$A(0)=-1$, the pressure still has a maximum on ![]() $y=0$ but
$y=0$ but ![]() $F(t)=-A(t)={1}/({1+2t})$ and thus the free boundary moves towards
$F(t)=-A(t)={1}/({1+2t})$ and thus the free boundary moves towards ![]() $y=0$ as
$y=0$ as ![]() $t\rightarrow \infty$.
$t\rightarrow \infty$.
2.1.1. The case of  $d$ large and
$d$ large and  $0< t<\frac {1}{2}$
$0< t<\frac {1}{2}$
A limit that leads to tractable asymptotic solutions occurs when ![]() $d$ is large. In this case we write
$d$ is large. In this case we write ![]() $\epsilon =1/d$ and, when
$\epsilon =1/d$ and, when ![]() $x,y$ are
$x,y$ are ![]() $O(1)$, the solution (2.6) will hold to lowest order. This is no longer true as
$O(1)$, the solution (2.6) will hold to lowest order. This is no longer true as ![]() $|x|\rightarrow \infty$ and so we need to introduce an outer region which is of width
$|x|\rightarrow \infty$ and so we need to introduce an outer region which is of width ![]() $O(\epsilon ^{-1})$ in the
$O(\epsilon ^{-1})$ in the ![]() $x$-direction while
$x$-direction while ![]() $y$ remains of
$y$ remains of ![]() $O(1)$. Thus with
$O(1)$. Thus with ![]() $X=\epsilon x, \varPhi ={\epsilon }^2 \phi$, the problem becomes
$X=\epsilon x, \varPhi ={\epsilon }^2 \phi$, the problem becomes
with, on the free boundary, now denoted by ![]() $y=F(X,t)$,
$y=F(X,t)$,
 \begin{equation} \epsilon^2\left(\frac{\partial \varPhi}{\partial t}+\frac{1}{2}\left(\frac{\partial \varPhi}{\partial X}\right)^2\right)+ \frac{1}{2}\left(\frac{\partial \varPhi}{\partial y}\right)^2 = 0, \end{equation}
\begin{equation} \epsilon^2\left(\frac{\partial \varPhi}{\partial t}+\frac{1}{2}\left(\frac{\partial \varPhi}{\partial X}\right)^2\right)+ \frac{1}{2}\left(\frac{\partial \varPhi}{\partial y}\right)^2 = 0, \end{equation}and
Also, at ![]() $t=0$, expanding the term in brackets in (2.4) for large
$t=0$, expanding the term in brackets in (2.4) for large ![]() $d$ and using (2.5) gives
$d$ and using (2.5) gives
Finally, matching with the solution (2.6) gives that, as ![]() $X\rightarrow 0$,
$X\rightarrow 0$,
When we now expand in the form
we find that, for some functions ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$,
$\beta$,
where, from (2.12b), ![]() $\alpha (X,0)=0$ and
$\alpha (X,0)=0$ and ![]() $\beta (X,0)=-({X^2}/({1+X^2}))$. Then conditions (2.10) and (2.11) imply that
$\beta (X,0)=-({X^2}/({1+X^2}))$. Then conditions (2.10) and (2.11) imply that ![]() $\alpha (X,t)=0$ and so
$\alpha (X,t)=0$ and so ![]() $\varPhi _0$ is independent of
$\varPhi _0$ is independent of ![]() $y$. In order to determine
$y$. In order to determine ![]() $\varPhi _0$, we need to proceed to the second-order terms in (2.10) which reveals that
$\varPhi _0$, we need to proceed to the second-order terms in (2.10) which reveals that
with the initial condition from (2.12b) that
Charpit's equations for (2.16) show that ![]() $P={\partial \varPhi _0}/{\partial t}$ and
$P={\partial \varPhi _0}/{\partial t}$ and ![]() $Q={\partial \varPhi _0}/{\partial X}$ are constant on the characteristics of (2.16) through the point
$Q={\partial \varPhi _0}/{\partial X}$ are constant on the characteristics of (2.16) through the point ![]() $X=X_0$,
$X=X_0$, ![]() $t=0$ and these characteristics are the particle paths given by
$t=0$ and these characteristics are the particle paths given by ![]() ${{\rm d}X}/{{\rm d}t}=Q$. Hence
${{\rm d}X}/{{\rm d}t}=Q$. Hence
and
where
The free surface can now be derived from (2.11) in the form
where
and ![]() $c_0$ and
$c_0$ and ![]() $c_1$ are functions of integration. However, the fact that the velocity is zero at infinity ensures that
$c_1$ are functions of integration. However, the fact that the velocity is zero at infinity ensures that ![]() $c_0(X,t)=0$.
$c_0(X,t)=0$.
We note that the characteristics of (2.21) are also the particle paths. Hence it is now convenient to change from Eulerian coordinates ![]() $(X,t)$ to Lagrangian coordinates
$(X,t)$ to Lagrangian coordinates ![]() $(X_0,t)$. Using (2.20), we see that, in Lagrangian coordinates with
$(X_0,t)$. Using (2.20), we see that, in Lagrangian coordinates with ![]() $t$ held constant,
$t$ held constant,
Hence, from (2.18),
and (2.21) becomes
Then, using the condition ![]() $F_0=1$ at
$F_0=1$ at ![]() $t=0$, we obtain
$t=0$, we obtain
 \begin{equation} F_0 =\frac{1}{\left(1-\dfrac{2t(1-3{X_0}^2)}{(1+{X_0}^2)^3}\right)}, \end{equation}
\begin{equation} F_0 =\frac{1}{\left(1-\dfrac{2t(1-3{X_0}^2)}{(1+{X_0}^2)^3}\right)}, \end{equation}
where (2.20) relates ![]() $X,t$ and
$X,t$ and ![]() $X_0$. Note that (2.26) and (2.19) match with (2.13a,b) as
$X_0$. Note that (2.26) and (2.19) match with (2.13a,b) as ![]() $X\rightarrow 0$ with
$X\rightarrow 0$ with ![]() $t<1/2$. Typical profiles for
$t<1/2$. Typical profiles for ![]() $F_0$ are shown in figure 2.
$F_0$ are shown in figure 2.

Figure 2. Value of ![]() $F_0$ defined by (2.26), plotted as a function of
$F_0$ defined by (2.26), plotted as a function of ![]() $X$ for
$X$ for ![]() $t=0,0.1,0.2,0.3$.
$t=0,0.1,0.2,0.3$.
It is relatively easy to show that ![]() $F_0$ always has a minimum at
$F_0$ always has a minimum at ![]() $X_0=1$ and then approaches
$X_0=1$ and then approaches ![]() $1$ from below as
$1$ from below as ![]() $|X_0|\rightarrow \infty$, as shown in figure 2. Most importantly, when
$|X_0|\rightarrow \infty$, as shown in figure 2. Most importantly, when ![]() $X_0=0$ we have
$X_0=0$ we have ![]() $X=0$ and
$X=0$ and ![]() $F_0={1}/({1-2t})$ and so the extreme tip of the jet goes to infinity in finite time in the large
$F_0={1}/({1-2t})$ and so the extreme tip of the jet goes to infinity in finite time in the large ![]() $d$ limit. Moreover, using (2.2), (2.16) and (2.22), we find that, to lowest order in
$d$ limit. Moreover, using (2.2), (2.16) and (2.22), we find that, to lowest order in ![]() $\epsilon$,
$\epsilon$,
 \begin{equation} -p ={-}\frac{1}{2}y^2 \frac{\partial ^3 \varPhi_0}{\partial X^2\partial t}+ \frac{\partial c_1}{\partial t}+ \frac{\partial \varPhi_0}{\partial X}\left(-\frac{1}{2}y^2\frac{\partial ^3 \varPhi_0}{\partial X^3}+ \frac{\partial c_1}{\partial X}\right)+\frac{1}{2}y^2\left(\frac{\partial ^2\varPhi_0}{\partial X^2}\right)^2. \end{equation}
\begin{equation} -p ={-}\frac{1}{2}y^2 \frac{\partial ^3 \varPhi_0}{\partial X^2\partial t}+ \frac{\partial c_1}{\partial t}+ \frac{\partial \varPhi_0}{\partial X}\left(-\frac{1}{2}y^2\frac{\partial ^3 \varPhi_0}{\partial X^3}+ \frac{\partial c_1}{\partial X}\right)+\frac{1}{2}y^2\left(\frac{\partial ^2\varPhi_0}{\partial X^2}\right)^2. \end{equation}Using (2.16), this reduces to
 \begin{equation} -p = y^2\left(\frac{\partial ^2\varPhi_0}{\partial X^2}\right)^2 + \frac{\partial c_1}{\partial t} + \frac{\partial \varPhi_0}{\partial X}\frac{\partial c_1}{\partial X}. \end{equation}
\begin{equation} -p = y^2\left(\frac{\partial ^2\varPhi_0}{\partial X^2}\right)^2 + \frac{\partial c_1}{\partial t} + \frac{\partial \varPhi_0}{\partial X}\frac{\partial c_1}{\partial X}. \end{equation}
Since ![]() $p=0$ on
$p=0$ on ![]() $y=F_0$, this means that
$y=F_0$, this means that
 \begin{equation} \frac{\partial c_1}{\partial t} + \frac{\partial \varPhi_0}{\partial X}\frac{\partial c_1}{\partial X} ={-}{F_0}^2\left(\frac{\partial ^2\varPhi_0}{\partial X^2}\right)^2, \end{equation}
\begin{equation} \frac{\partial c_1}{\partial t} + \frac{\partial \varPhi_0}{\partial X}\frac{\partial c_1}{\partial X} ={-}{F_0}^2\left(\frac{\partial ^2\varPhi_0}{\partial X^2}\right)^2, \end{equation}and hence that
 \begin{equation} p = \left(\frac{\partial ^2\varPhi_0}{\partial X^2}\right)^2({F_0}^2-y^2). \end{equation}
\begin{equation} p = \left(\frac{\partial ^2\varPhi_0}{\partial X^2}\right)^2({F_0}^2-y^2). \end{equation}
Thus, pressure maxima in this regime can only occur on ![]() $y=0$.
$y=0$.
Using (2.24), we see that the pressure on ![]() $y=0$ is a function of
$y=0$ is a function of ![]() $X$, as shown in figure 3. Moreover, since
$X$, as shown in figure 3. Moreover, since ![]() $X$ is a monotone increasing function of
$X$ is a monotone increasing function of ![]() $X_0$,
$X_0$, ![]() $p$ will now have two maxima in
$p$ will now have two maxima in ![]() $X\geq 0$, with the maximum at
$X\geq 0$, with the maximum at ![]() $X=0$ being increasingly dominant as
$X=0$ being increasingly dominant as ![]() $t\rightarrow \tfrac {1}{2}$. We remark that the weaker maximum is generated by our initial conditions and is not associated with a stagnation-point flow.
$t\rightarrow \tfrac {1}{2}$. We remark that the weaker maximum is generated by our initial conditions and is not associated with a stagnation-point flow.

Figure 3. Value of ![]() $p(X,0)$ plotted from (2.30) for
$p(X,0)$ plotted from (2.30) for ![]() $t=0.01$.
$t=0.01$.
The behaviour revealed in figure 3 enables us to draw the isobars in ![]() $X \geq 0, y \geq 0$ as shown in figure 4. The isobars in
$X \geq 0, y \geq 0$ as shown in figure 4. The isobars in ![]() $y<0$ are the mirror image of those in
$y<0$ are the mirror image of those in ![]() $y>0$ until the zero-pressure isobar is reached and the pressure is everywhere negative below this isobar.
$y>0$ until the zero-pressure isobar is reached and the pressure is everywhere negative below this isobar.

Figure 4. Isobars of ![]() $p(X,y)$ for
$p(X,y)$ for ![]() $t=0.3$ when
$t=0.3$ when ![]() $y>0$; the fluid region is shaded.
$y>0$; the fluid region is shaded.
2.1.2. The limit as  $t\uparrow \frac {1}{2}$
$t\uparrow \frac {1}{2}$
We observe that, when ![]() $X_0$ and
$X_0$ and ![]() $\tfrac {1}{2}-t=\tau$ are small, (2.19) and (2.26) give
$\tfrac {1}{2}-t=\tau$ are small, (2.19) and (2.26) give
Hence, the solution is singular as ![]() $X_0,\tau \rightarrow 0$ and rapid changes are expected when
$X_0,\tau \rightarrow 0$ and rapid changes are expected when ![]() $\tau$ and
$\tau$ and ![]() ${X_0}^2$ are small and comparable. If we assume that
${X_0}^2$ are small and comparable. If we assume that ![]() $\tau =O({\hat {\epsilon }}^2)$ and
$\tau =O({\hat {\epsilon }}^2)$ and ![]() $X_0=O(\hat {\epsilon })$ for some small parameter
$X_0=O(\hat {\epsilon })$ for some small parameter ![]() $\hat {\epsilon }$, then the appropriate scalings in this region are
$\hat {\epsilon }$, then the appropriate scalings in this region are
and this leads to a region where Laplace's equation (2.1) holds if ![]() $\hat {\epsilon } = \epsilon ^{1/5}$. Thus we write
$\hat {\epsilon } = \epsilon ^{1/5}$. Thus we write
The resulting free-boundary problem is equivalent to the full problem (2.1) with boundary conditions (2.2) and (2.3) but with the solution matching with (2.31a–c) as ![]() $\hat {x}\rightarrow \infty$. If we let
$\hat {x}\rightarrow \infty$. If we let ![]() $X_0\rightarrow 0$ in (2.31a–c) while keeping
$X_0\rightarrow 0$ in (2.31a–c) while keeping ![]() $\tau$ constant we see that, for
$\tau$ constant we see that, for ![]() $t<\frac {1}{2}$,
$t<\frac {1}{2}$,
as ![]() $\hat {x} \rightarrow \infty$. As
$\hat {x} \rightarrow \infty$. As ![]() $\hat {\tau } \rightarrow \infty$, we need to match with (2.6) and hence the solution is
$\hat {\tau } \rightarrow \infty$, we need to match with (2.6) and hence the solution is
which is equivalent to the limit of (2.6) as ![]() $t\uparrow 1/2$. Thus, to lowest order in
$t\uparrow 1/2$. Thus, to lowest order in ![]() $\epsilon$, the jet extends to infinity at
$\epsilon$, the jet extends to infinity at ![]() $\hat {\tau } = 0$. As noted after (2.8), the lowest-order pressure maintains a maximum along
$\hat {\tau } = 0$. As noted after (2.8), the lowest-order pressure maintains a maximum along ![]() $y=0$.
$y=0$.
2.2. The case of  $d$ finite and
$d$ finite and  $t\ll 1$
$t\ll 1$
(i)
 $d>1$ We will consider only the small-time solution of (2.1), (2.2), (2.3) and (2.4) for
$d>1$ We will consider only the small-time solution of (2.1), (2.2), (2.3) and (2.4) for  $d>1$. Assuming a smooth dependence on time, we seek expansions of the form
(2.36)and
$d>1$. Assuming a smooth dependence on time, we seek expansions of the form
(2.36)and \begin{equation} \displaystyle\phi\sim\phi(x,y,0)+t{\phi}_1(x,y)+\cdots , \end{equation}(2.37)Then we find that
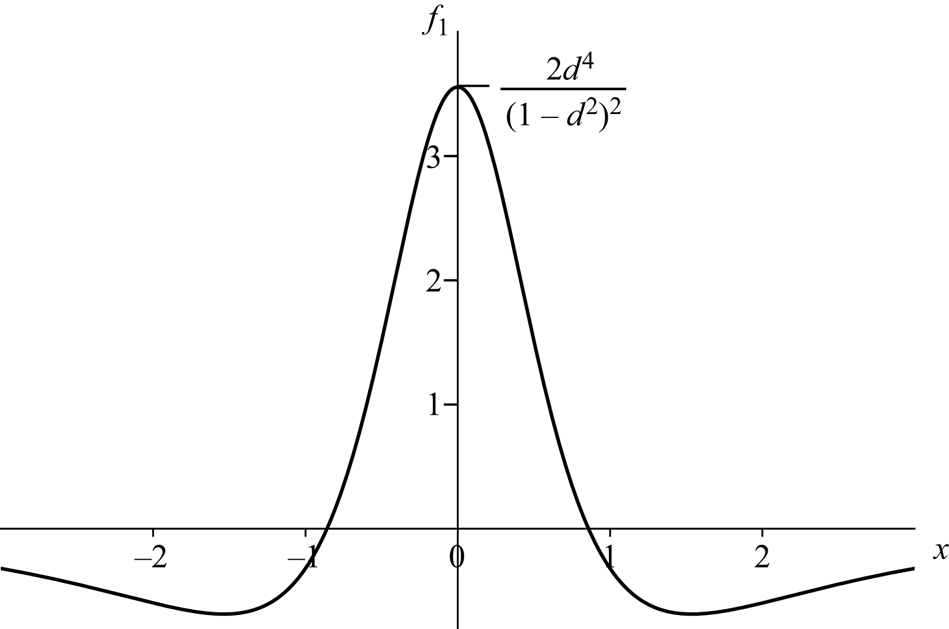
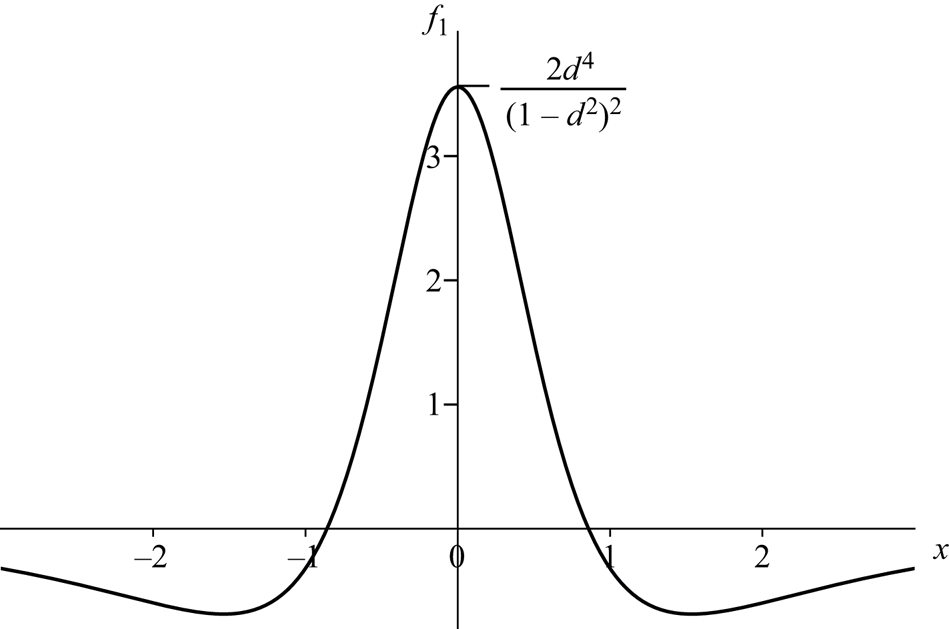
\begin{equation} \displaystyle\phi\sim\phi(x,y,0)+t{\phi}_1(x,y)+\cdots , \end{equation}(2.37)Then we find that \begin{equation} \displaystyle f\sim1+tf_1(x)+\cdots . \end{equation}(2.38)and we see that the free surface immediately adopts the jet profile shown in figure 5. The zeros of
\begin{equation} \displaystyle f\sim1+tf_1(x)+\cdots . \end{equation}(2.38)and we see that the free surface immediately adopts the jet profile shown in figure 5. The zeros of \begin{equation} f_1=\frac{\partial
\phi(x,y,0)}{\partial y}|_{y=1}=
\frac{-2d^4(3x^4+2(1+d^2)x^2-(1-d^2)^2)}{(x^2+(1-d)^2)^2(x^2+(1+d)^2)^2},
\end{equation}
\begin{equation} f_1=\frac{\partial
\phi(x,y,0)}{\partial y}|_{y=1}=
\frac{-2d^4(3x^4+2(1+d^2)x^2-(1-d^2)^2)}{(x^2+(1-d)^2)^2(x^2+(1+d)^2)^2},
\end{equation}
 $f_1$ are where
$f_1$ are where  $3x^2=2\sqrt {1-d^2+d^4}-1-d^2$ and
$3x^2=2\sqrt {1-d^2+d^4}-1-d^2$ and  $f_1(0)={2d^4}/{(1-d^2)^2}$. However, the lowest-order pressure can only be calculated by finding
$f_1(0)={2d^4}/{(1-d^2)^2}$. However, the lowest-order pressure can only be calculated by finding  $\phi _1$, which involves solving a complicated potential problem which will not be addressed here. We also note that figure 5 has the same geometrical features as were seen in the longer-time solutions shown in figure 2.
$\phi _1$, which involves solving a complicated potential problem which will not be addressed here. We also note that figure 5 has the same geometrical features as were seen in the longer-time solutions shown in figure 2.(ii)
 $d\downarrow 1$ The profile (2.38) tends to infinity as
$d\downarrow 1$ The profile (2.38) tends to infinity as  $x\rightarrow 0$ when
$x\rightarrow 0$ when  $d=1$ and hence, to understand what happens as
$d=1$ and hence, to understand what happens as  $\delta = d-1$ tends to zero, we expand (2.4) by writing
(2.39a,b)and, noting that there is only one effective dipole in this region, (2.38) gives that, at
$\delta = d-1$ tends to zero, we expand (2.4) by writing
(2.39a,b)and, noting that there is only one effective dipole in this region, (2.38) gives that, at \begin{equation} y= 1 + \delta \tilde{y}, \quad x = \delta \tilde{x}, \end{equation}
\begin{equation} y= 1 + \delta \tilde{y}, \quad x = \delta \tilde{x}, \end{equation} $t=0$,
(2.40)Hence, for
$t=0$,
(2.40)Hence, for \begin{equation} \phi \sim{-}\frac{\tilde{y}-1}{2\delta ({\tilde{x}}^2 + (\tilde{y} - 1)^2)} + O(1). \end{equation}
\begin{equation} \phi \sim{-}\frac{\tilde{y}-1}{2\delta ({\tilde{x}}^2 + (\tilde{y} - 1)^2)} + O(1). \end{equation} $t$ of
$t$ of  $o({\delta }^2)$,
(2.41)In this short time-scale regime, the free boundary is still of the same form as in figure 5 and the length of the jet is
$o({\delta }^2)$,
(2.41)In this short time-scale regime, the free boundary is still of the same form as in figure 5 and the length of the jet is \begin{equation} f_1 \sim{-}\frac{({\tilde{x}}^2 - 1)}{2\delta^2 (1+{\tilde{x}}^2)^2} + O(1). \end{equation}
\begin{equation} f_1 \sim{-}\frac{({\tilde{x}}^2 - 1)}{2\delta^2 (1+{\tilde{x}}^2)^2} + O(1). \end{equation} ${t}/{2\delta ^2}$ while its width is of
${t}/{2\delta ^2}$ while its width is of  $O(\delta )$.
$O(\delta )$.

Figure 5. Value of
 $f_1$ plotted as a function of
$f_1$ plotted as a function of  $x$ from (2.38).
$x$ from (2.38).In summary, we have shown that, when
 $d$ is either near to unity or tends to infinity, the formal asymptotic analysis suggests that the interface tends to infinity in a finite time. In both cases the free surface is focussed into a jet which contains 4 inflection points, as shown in figures 2 and 5.
$d$ is either near to unity or tends to infinity, the formal asymptotic analysis suggests that the interface tends to infinity in a finite time. In both cases the free surface is focussed into a jet which contains 4 inflection points, as shown in figures 2 and 5.
We now turn to the axisymmetric case, which will be found to lead to similar consequences but with even stronger jet accelerations.
3. The axisymmetric problem
This section will describe the straightforward generalisation of the asymptotic analysis in § 2 to the case of axisymmetric jets with a far-field dipole. Only the principal equations and results will be stated by using relevant analogies from § 2; the same notation will be used for the velocity potential and the free surface profile.
In radial polar coordinates ![]() $(r,z)$, the model is
$(r,z)$, the model is
with, on ![]() $z=f(r,t)$,
$z=f(r,t)$,
 \begin{equation} \frac{\partial \phi}{\partial t}+\frac{1}{2}\left(\left(\frac{\partial \phi}{\partial r}\right)^2+ \left(\frac{\partial \phi}{\partial z}\right)^2\right)=0, \end{equation}
\begin{equation} \frac{\partial \phi}{\partial t}+\frac{1}{2}\left(\left(\frac{\partial \phi}{\partial r}\right)^2+ \left(\frac{\partial \phi}{\partial z}\right)^2\right)=0, \end{equation}and
Also, at ![]() $t=0$,
$t=0$,
which is the analogue of (2.4) with ![]() $\epsilon =d^{-1}$, and
$\epsilon =d^{-1}$, and
When ![]() $\epsilon = 0$, the analogue of (2.6) is
$\epsilon = 0$, the analogue of (2.6) is
Thus the eventual acceleration of the interface is an order of magnitude greater than in the two-dimensional case.
3.1. The solution for small  $\epsilon$
$\epsilon$
When ![]() $z=O(1)$ and
$z=O(1)$ and ![]() $r=O(\epsilon ^{-1})$, we write
$r=O(\epsilon ^{-1})$, we write ![]() $r=R/\epsilon$ and
$r=R/\epsilon$ and ![]() $\phi =\varPhi /\epsilon ^2$ so that
$\phi =\varPhi /\epsilon ^2$ so that
with, on ![]() $z=F(R,t)$,
$z=F(R,t)$,
 \begin{equation} \frac{1}{2}\left(\frac{\partial \varPhi}{\partial z}\right)^2 + \epsilon^2\left( \frac{1}{2}\left(\frac{\partial \varPhi}{\partial R}\right)^2+\frac{\partial \varPhi}{\partial t}\right) = 0, \end{equation}
\begin{equation} \frac{1}{2}\left(\frac{\partial \varPhi}{\partial z}\right)^2 + \epsilon^2\left( \frac{1}{2}\left(\frac{\partial \varPhi}{\partial R}\right)^2+\frac{\partial \varPhi}{\partial t}\right) = 0, \end{equation}and
Writing
and
the lowest-order solution gives ![]() $\varPhi _0$ as a function of
$\varPhi _0$ as a function of ![]() $R,t$ only, and such that
$R,t$ only, and such that
The initial conditions are
and the analogue of (2.21) is
and again ![]() $c_0(R,t)$ has to vanish since there is no mean flow at infinity. The relevant solution of (3.12) is
$c_0(R,t)$ has to vanish since there is no mean flow at infinity. The relevant solution of (3.12) is
where
and ![]() $R_0$ is a parameter analogous to
$R_0$ is a parameter analogous to ![]() $X_0$ in two dimensions. Then,
$X_0$ in two dimensions. Then, ![]() $F_0$ is determined in terms of the Lagrangian variables
$F_0$ is determined in terms of the Lagrangian variables ![]() $R_0,t$ from (3.14) in the form
$R_0,t$ from (3.14) in the form
where
and
Hence, ![]() $F_0$ has a time dependence that is different from that in (2.26), namely
$F_0$ has a time dependence that is different from that in (2.26), namely
so that ![]() $F_0$ grows like
$F_0$ grows like ![]() $(1-t)^{-2}$ as
$(1-t)^{-2}$ as ![]() $t\uparrow 1$ when
$t\uparrow 1$ when ![]() $R=0$. A typical profile for
$R=0$. A typical profile for ![]() $F_0$ is shown in figure 6, which is geometrically similar to figure 2. However, when we calculate
$F_0$ is shown in figure 6, which is geometrically similar to figure 2. However, when we calculate ![]() $p$ as we did to derive (2.30), we find that
$p$ as we did to derive (2.30), we find that
 \begin{equation} p = \left( \left(\frac{\partial ^2 \varPhi_0}{\partial R^2}\right)^2 + \frac{1}{R}\frac{\partial \varPhi_0}{\partial R}\frac{\partial ^2 \varPhi_0}{\partial R^2} + \frac{1}{R^2}\left(\frac{\partial \varPhi_0}{\partial R}\right)^2\right)({F_0}^2-z^2). \end{equation}
\begin{equation} p = \left( \left(\frac{\partial ^2 \varPhi_0}{\partial R^2}\right)^2 + \frac{1}{R}\frac{\partial \varPhi_0}{\partial R}\frac{\partial ^2 \varPhi_0}{\partial R^2} + \frac{1}{R^2}\left(\frac{\partial \varPhi_0}{\partial R}\right)^2\right)({F_0}^2-z^2). \end{equation}
The leading bracket is positive for all ![]() $R\geq 0$ and hence the only maximum of
$R\geq 0$ and hence the only maximum of ![]() $p$ is at
$p$ is at ![]() $R=0, z=0$.
$R=0, z=0$.

Figure 6. Value of ![]() $F_0$ plotted from (3.20) as a function of
$F_0$ plotted from (3.20) as a function of ![]() $R$ for
$R$ for ![]() $t=0,0.1,0.2,0.3,0.5,0.75$.
$t=0,0.1,0.2,0.3,0.5,0.75$.
As for the two-dimensional case, if we let ![]() $R_0\rightarrow 0$ and
$R_0\rightarrow 0$ and ![]() $t\rightarrow 1$, we find, from (3.15), (3.16) and (3.20) that, the scalings in (2.33a–e) need to be modified. For (3.1), (3.2), (3.3) the appropriate scalings are
$t\rightarrow 1$, we find, from (3.15), (3.16) and (3.20) that, the scalings in (2.33a–e) need to be modified. For (3.1), (3.2), (3.3) the appropriate scalings are
This means that ![]() $\phi$ still satisfies Laplace's equation and when we apply the matching condition analogous to (2.34a,b), the resulting lowest-order solution in this region emerges as the limit of (3.6) as
$\phi$ still satisfies Laplace's equation and when we apply the matching condition analogous to (2.34a,b), the resulting lowest-order solution in this region emerges as the limit of (3.6) as ![]() $t\uparrow 1$, namely
$t\uparrow 1$, namely
 \begin{equation} \phi = \frac{z^2-\dfrac{1}{2}r^2}{1-t} - \frac{3}{5(1-t)^5} \quad \text{and} \quad f=\frac{1}{(1-t)^2}. \end{equation}
\begin{equation} \phi = \frac{z^2-\dfrac{1}{2}r^2}{1-t} - \frac{3}{5(1-t)^5} \quad \text{and} \quad f=\frac{1}{(1-t)^2}. \end{equation}
Finally, we note that a small-time analysis when ![]() $d=O(1)$ again leads to a profile similar to that in figure 5 and that if we set
$d=O(1)$ again leads to a profile similar to that in figure 5 and that if we set ![]() $d=1+\delta$ where
$d=1+\delta$ where ![]() $\delta$ is small, then, for small times the jet length is of
$\delta$ is small, then, for small times the jet length is of ![]() $O({t}/{{\delta }^3})$ as
$O({t}/{{\delta }^3})$ as ![]() $\delta \rightarrow 0$, which is an order of magnitude longer than that in the two-dimensional case. This is to be expected since there is now flow into the jet from all directions.
$\delta \rightarrow 0$, which is an order of magnitude longer than that in the two-dimensional case. This is to be expected since there is now flow into the jet from all directions.
4. Conclusion
This paper presents asymptotic evidence to suggest that, when a pressure maximum is close to a planar free boundary of an inviscid fluid in the absence of gravity, the surface can develop a fast jet. When the jets are driven by dipoles, they accelerate to become of infinite length in a finite time which becomes shorter as the initial distance between the dipoles decreases. The theory is described in both two dimensions and three dimensions and it is shown that axisymmetric jets accelerate faster than those in two dimensions.
These predictions are based on asymptotic analyses that only apply for certain stages of the jet evolution and numerical solutions are needed to corroborate our predictions and complete the picture.
Acknowledgements
The authors are grateful to Professor G. Sander for numerous helpful conversations and to M. Cotton who provided the figures.
Funding
This research received no specific grant from any funding agency, commercial or not-for-profit sectors.
Declaration of interests
The authors report no conflict of interest.