Hostname: page-component-6bf8c574d5-h6jzd Total loading time: 0.001 Render date: 2025-02-20T10:58:15.808Z Has data issue: false hasContentIssue false
  • English
  • Français

Instability of plumes driven by localized heating

Published online by Cambridge University Press:  13 November 2013

Juan M. Lopez  and
Francisco Marques
Juan M. Lopez*
Affiliation:
School of Mathematical and Statistical Sciences, Arizona State University, Tempe, AZ 85287, USA
Francisco Marques
Affiliation:
Departament de Física Aplicada, Universidad Politècnica de Catalunya, Barcelona 08034, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Plumes due to localized buoyancy sources are of wide interest owing to their prevalence in many situations. This study investigates the transition from laminar to turbulent dynamics. Several experiments have reported that this transition is sensitive to external perturbations. As such, a well-controlled set-up has been chosen for our numerical study, consisting of a localized heat source at the bottom of an enclosed cylinder whose walls are all maintained at a fixed uniform temperature, except for the localized heat source. At moderate Rayleigh numbers 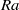$\mathit{Ra}$, the flow consists of a steady, axisymmetric purely poloidal plume. On increasing 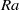$\mathit{Ra}$, the flow undergoes a supercritical Hopf bifurcation to an axisymmetric ‘puffing’ plume, where a vortex ring is periodically emitted from the localized heater. At higher 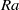$\mathit{Ra}$, this state becomes unstable to a sequence of symmetry-breaking bifurcations, going through a quasi-periodic ‘fluttering’ stage where the axisymmetric rings are tilted, and other states in which the sequence of tilted rings interact with each other. The sequence of symmetry-breaking bifurcations in the transition to turbulence culminates in a torus breakup event in which all the spatial and spatio-temporal symmetries of the system are broken.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Instability: Nonlinear instability Convection: Plumes/thermals
Type
Papers
Information
Journal of Fluid Mechanics , Volume 736 , 10 December 2013 , pp. 616 - 640
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G. 2009 Turbulent convection. Physics 2, 74.Google Scholar
Ahlers, G., Grossman, S. & Lohse, D. 2009 Heat transfer and large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Altmeyer, S., Do, Y., Marques, F. & Lopez, J. M. 2012 Symmetry-breaking Hopf bifurcations to 1-, 2-, and 3-tori in small-aspect-ratio counterrotating Taylor–Couette flow. Phys. Rev. E 86, 046316.Google Scholar
Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.Google Scholar
Armbruster, D., Guckenheimer, J. & Holmes, P. 1988 Heteroclinic cycles and modulated travelling waves in systems with $O(2)$ symmetry. Physica D 29, 257–282.Google Scholar
Baines, W. D. & Turner, J. S. 1969 Turbulent buoyant convection from a source in a confined region. J. Fluid Mech. 37, 51–80.Google Scholar
Batchelor, G. K. & Gill, A. E. 1962 Analysis of the stability of axisymmetric jets. J. Fluid Mech. 14, 529–551.Google Scholar
Cetegen, B. M., Dong, Y. & Soteriou, M. C. 1998 Experiments on stability and oscillatory behaviour of planar buoyant plumes. Phys. Fluids 10, 1658–1665.Google Scholar
Chossat, P. & Lauterbach, R. 2000 Methods in Equivariant Bifurcations and Dynamical Systems. World Scientific.Google Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 21, 385–425.Google Scholar
Colomer, J., Boubnov, B. M. & Fernando, H. J. S. 1999 Turbulent convection from isolated sources. Dyn. Atmos. Oceans 30, 125–148.Google Scholar
Crawford, J. D. & Knobloch, E. 1988 Symmetry-breaking bifurcations in $O(2)$ maps. Phys. Lett. A 128, 327–331.CrossRefGoogle Scholar
Crawford, J. D. & Knobloch, E. 1991 Symmetry and symmetry-breaking bifurcations in fluid dynamics. Annu. Rev. Fluid Mech. 23, 341–387.CrossRefGoogle Scholar
Dangelmayr, G. & Knobloch, E. 1987 The Takens–Bogdanov bifurcation with $O(2)$ symmetry. Phil. Trans. R. Soc. Lond. A 322, 243–279.Google Scholar
DesJardin, P. E., O’Hern, T. J. & Tieszen, S. R. 2004 Large eddy simulation and experimental measurements of the near-field of a large turbulent helium plume. Phys. Fluids 16, 1866–1883.Google Scholar
Desrayaud, G. & Lauriat, G. 1993 Unsteady confined buoyant plumes. J. Fluid Mech. 252, 617–646.CrossRefGoogle Scholar
Do, Y., Lopez, J. M. & Marques, F. 2010 Optimal harmonic response in a confined Bödewadt boundary layer flow. Phys. Rev. E 82, 036301.Google Scholar
Dong, S. 2007 Direct numerical simulation of turbulent Taylor–Couette flow. J. Fluid Mech. 587, 373–393.Google Scholar
Dong, S. & Zheng, X. 2011 Direct numerical simulation of spiral turbulence. J. Fluid Mech. 668, 150–173.Google Scholar
Elicer-Cortés, J. C., Navia, A., Boyer, D., Pavageau, M. & Hernández, R. H. 2006 Experimental determination of preferred instability modes in a mechanically excited thermal plume by ultrasound scattering. Exp. Therm. Fluid Sci. 30, 355–365.Google Scholar
Fannelop, T. K. & Webber, D. M. 2003 On buoyant plumes rising from area sources in a calm environment. J. Fluid Mech. 497, 319–334.Google Scholar
Fay, J. A. 1973 Buoyant plumes and wakes. Annu. Rev. Fluid Mech. 5, 151–160.Google Scholar
Fornberg, B. 1998 A Practical Guide to Pseudospectral Methods. Cambridge University Press.Google Scholar
Gebhart, B. 1973 Instability, transition, and turbulence in buoyancy-induced flows. Annu. Rev. Fluid Mech. 5, 213–246.Google Scholar
Golubitsky, M. & Stewart, I. 2002 The Symmetry Perspective: From Equilbrium to Chaos in Phase Space and Physical Space. Birkhäuser.Google Scholar
Hama, F. R. 1962 Streaklines in a perturbed shear flow. Phys. Fluids 5, 644–650.Google Scholar
Haragus, M. & Iooss, G. 2011 Local Bifurcations, Center Manifolds, and Normal Forms in Infinite-Dimensional Dynamical Systems. Springer.Google Scholar
Hu, H. H. & Patankar, N. 1995 Non-axisymmetric instability of core-annular flow. J. Fluid Mech. 290, 213–224.Google Scholar
Hughes, S. & Randriamampianina, A. 1998 An improved projection scheme applied to pseudospectral methods for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 28, 501–521.Google Scholar
Jaluria, Y. & Gebhart, B. 1975 On the buoyancy-induced flow arising from a heated hemisphere. Intl J. Heat Mass Transfer 18, 415–431.Google Scholar
Jiang, X. & Luo, K. H. 2000 Direct numerical simulation of the puffing phenomenon of an axisymmetric thermal plume. Theor. Comput. Fluid Dyn. 14, 55–74.Google Scholar
Kaye, N. B. & Hunt, G. R. 2010 The effect of floor heat source area on the induced airflow in a room. Build. Environ. 45, 839–847.Google Scholar
Kimura, S. & Bejan, A. 1983 Mechanism for transition to turbulence in buoyant plume flow. Intl J. Heat Mass Transfer 26, 1515–1532.CrossRefGoogle Scholar
Knobloch, E. 1986 On the degenerate Hopf bifurcation with $O(2)$ symmetry. In Multiparameter Bifurcation Theory (ed. Golubitsky, M. & Guckenheimer, J.), Contemporary Mathematics, vol. 56, pp. 193–201. American Mathematical Society.Google Scholar
Knobloch, E. 1996 Symmetry and instability in rotating hydrodynamic and magnetohydrodynamic flows. Phys. Fluids 8, 1446–1454.Google Scholar
Krupa, M. 1990 Bifurcations of relative equilibria. SIAM J. Math. Anal. 21, 1453–1486.Google Scholar
Linden, P. F. 2000 Convection in the environment. In Perspectives in Fluid Dynamics (ed. Batchelor, G. K., Moffatt, H. K. & Worster, M. G.), pp. 289–345. Cambridge University Press.Google Scholar
List, E. J. 1982 Turbulent jets and plumes. Annu. Rev. Fluid Mech. 14, 189–212.CrossRefGoogle Scholar
Lopez, J. M. & Marques, F. 2009 Centrifugal effects in rotating convection: nonlinear dynamics. J. Fluid Mech. 628, 269–297.Google Scholar
Lopez, J. M. & Marques, F. 2010 Sidewall boundary layer instabilities in a rapidly rotating cylinder driven by a differentially co-rotating lid. Phys. Fluids 22, 114109.Google Scholar
Lopez, J. M. & Marques, F. 2011 Instabilities and inertial waves generated in a librating cylinder. J. Fluid Mech. 687, 171–193.CrossRefGoogle Scholar
Maleki, M., Habibi, M., Golestanian, R., Ribe, N. M. & Bonn, D. 2004 Liquid rope coiling on a solid surface. Phys. Rev. Lett. 93, 214502.CrossRefGoogle ScholarPubMed
Marques, F., Lopez, J. M. & Blackburn, H. M. 2004 Bifurcations in systems with ${Z}_{2} $ spatio-temporal and $O(2)$ spatial symmetry. Physica D 189, 247–276.CrossRefGoogle Scholar
Marques, F., Mercader, I., Batiste, O. & Lopez, J. M. 2007 Centrifugal effects in rotating convection: axisymmetric states and three-dimensional instabilities. J. Fluid Mech. 580, 303–318.Google Scholar
Massaguer, J. M., Mercader, I. & Net, M. 1990 Nonlinear dynamics of vertical vorticity in low-Prandtl number thermal convection. J. Fluid Mech. 214, 579–597.Google Scholar
Maxworthy, T. 1999 The flickering candle: transition to a global oscillation in a thermal plume. J. Fluid Mech. 390, 297–323.Google Scholar
Mercader, I., Batiste, O. & Alonso, A. 2010 An efficient spectral code for incompressible flows in cylindrical geometries. Comput. Fluids 39, 215–224.Google Scholar
Mercader, I., Net, M. & Falqués, A. 1991 Spectral methods for high order equations. Comput. Meth. Appl. Mech. Engng 91, 1245–1251.Google Scholar
Meseguer, A., Mellibovsky, F., Avila, M. & Marques, F. 2009 Instability mechanisms and transition scenarios of spiral turbulence in Taylor–Couette flow. Phys. Rev. E 80, 046315.Google Scholar
Mittal, R., Wilson, J. J. & Najjar, F. M. 2001 Symmetry properties of the transitional sphere wake. AIAA J. 40, 579–582.Google Scholar
Morton, B. R., Taylor, G. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Murphy, J. O. & Lopez, J. M. 1984 The influence of vertical vorticity on thermal convection. Austral. J. Phys. 37, 41–62.Google Scholar
Nagata, W. 1986 Unfoldings of degenerate Hopf bifurcations with $O(2)$ symmetry. Dyn. Stab. Syst. 1, 125–157.Google Scholar
Navarro, M. C. & Herrero, H. 2011 Vortex generation by a convective instability in a cylindrical annulus non-homogeneously heated. Physica D 240, 1181–1188.Google Scholar
Orszag, S. A. & Patera, A. T. 1983 Secondary instability of wall-bounded shear flows. J. Fluid Mech. 128, 347–385.Google Scholar
Pham, M. V., Plourde, F. & Doan, S. K. 2007 Direct and large-eddy simulations of a pure thermal plume. Phys. Fluids 19, 125103.Google Scholar
Pham, M. V., Plourde, F. & Kim, S. D. 2005 Three-dimensional characterization of a pure thermal plume. J. Heat Transfer 127, 624–636.Google Scholar
Plourde, F., Pham, M. V., Kim, S. D. & Balachandar, S. 2008 Direct numerical simulations of a rapidly expanding thermal plume: structure and entrainment interaction. J. Fluid Mech. 604, 99–123.CrossRefGoogle Scholar
Siggia, E. D. 1994 High Rayleigh number convection. Annu. Rev. Fluid Mech. 26, 137–168.Google Scholar
Soteriou, M. C., Dong, Y. & Cetegen, B. M. 2002 Lagrangian simulation of the unsteady near field dynamics of planar buoyant plumes. Phys. Fluids 14, 3118–3140.Google Scholar
Tomboulides, A. G. & Orszag, S. A. 2000 Numerical investigation of transitional and weak turbulent flow past a sphere. J. Fluid Mech. 416, 45–73.Google Scholar
Torrance, K. E. 1979 Natural convection in thermally stratified enclosures with localized heating from below. J. Fluid Mech. 95, 477–495.Google Scholar
Torrance, K. E., Orloff, L. & Rockett, J. A. 1969 Experiments on natural convection in enclosures with localized heating from below. J. Fluid Mech. 36, 21–31.Google Scholar
Torrance, K. E. & Rockett, J. A. 1969 Numerical study of natural convection in an enclosure with localized heating from below – creeping flow to the onset of laminar instability. J. Fluid Mech. 36, 33–54.Google Scholar
Turner, J. S. 1969 Buoyant plumes and thermals. Annu. Rev. Fluid Mech. 1, 29–44.Google Scholar
Ulucaki, M. E. 1996 Turbulent natural convection in an enclosure with localized heating from below. Exp. Heat Transfer 9, 305–321.Google Scholar
Williams, T. C., Shaddix, C. R., Schefer, R. W. & Desgroux, P. 2007 The response of buoyant laminar diffusion flames to low-frequency forcing. Combust. Flame 151, 676–684.Google Scholar
Woods, A. W. 2010 Turbulent plumes in nature. Annu. Rev. Fluid Mech. 42, 391–412.Google Scholar
Yang, H. Q. 1992 Buckling of a thermal plume. Intl J. Heat Mass Transfer 35, 1527–1532.CrossRefGoogle Scholar

Lopez and Marques supplementary movies

Isotherms over one period of the axisymmetric periodic state at $Ra=5\times 10^7$.

Download Lopez and Marques supplementary movies(Video)
Video 1.2 MB

Lopez and Marques supplementary movies

Azimuthal vorticity over one period of the axisymmetric periodic state at $Ra=5\times 10^7$.

Download Lopez and Marques supplementary movies(Video)
Video 1.1 MB

Lopez and Marques supplementary movies

Isosurfaces of the azimuthal vorticity of the plume at $Ra=5.5\times 10^7$.

Download Lopez and Marques supplementary movies(Video)
Video 314.5 KB

Lopez and Marques supplementary movies

Isosurfaces of axial vorticity f the plume at $Ra=5.5\times 10^7$.

Download Lopez and Marques supplementary movies(Video)
Video 486.6 KB

Lopez and Marques supplementary movies

Isosurfaces of the azimuthal vorticity at $Ra=7\times 10^7$.

Download Lopez and Marques supplementary movies(Video)
Video 135 KB

Lopez and Marques supplementary movies

Isosurfaces of the azimuthal vorticity at $Ra=3\times 10^8$.

Download Lopez and Marques supplementary movies(Video)
Video 787.8 KB