Instability of falling films of discontinuously shear-thickening fluid

Abstract

Aqueous suspensions of cornstarch abruptly increase their viscosity on raising either shear rate or stress, and display the formation of large-amplitude waves when flowing down inclined channels. The two features have been recently connected using constitutive models designed to describe discontinuous shear thickening. By including time-dependent relaxation and spatial diffusion of the frictional contact density responsible for shear thickening, an analysis of steady sheet flow and its linear stability is presented. The inclusion of such effects is motivated by the need to avoid an ill-posed mathematical problem in thin-film theory and the resulting failure to select any preferred wavelength for unstable linear waves. Relaxation, in particular, eliminates an ultraviolet catastrophe in the spectrum of unstable waves and furnishes a preferred wavelength at which growth is maximized. The nonlinear dynamics of the unstable waves is briefly explored. It is found that the linear instability saturates once disturbances reach finite amplitude, creating steadily propagating nonlinear waves. These waves take the form of a series of steep, shear-thickened steps that translate relatively slowly in comparison with the mean flow.

1. Introduction

In his book on Gravity Currents, Simpson (1999) reported an interesting observation of the formation of large-amplitude waves on relatively slowly flowing layers of aqueous suspensions of cornstarch. This observation was subsequently taken up by Balmforth, Bush & Craster (2005) who conducted more experiments and provided details of the phenomenology. They concluded that the waves arose from a linear instability at surprisingly low Reynolds number, unlike in the classical Kapitza problem for roll waves on flowing films of viscous and other fluids, where critical Reynolds numbers are of order unity (e.g. Chang 1994; Ng & Mei 1994; Balmforth & Liu 2004). Unfortunately, Balmforth et al. were unable to provide a complementary theoretical explanation, primarily because a detailed constitutive law describing the rheology of cornstach suspensions was not available at the time. Existing models for viscoelastic liquids or generalized Newtonian fluids either did not match the known properties of such suspensions or could not explain instability at such seemingly low Reynolds numbers. Consequently, Balmforth et al. left the question of the origin of the waves unresolved, failing to decipher how the instability reflected the material behaviour, or rheology, of cornstarch suspensions.

Much more recently, Darbois Texier et al. have returned to the problem, providing a comprehensive review and perspective that repositions it into current context (see Darbois Texier et al. 2020, 2023 and references therein). They advanced the first theoretical rationalization of the origin of the waves, and compared predictions with further laboratory experiments. For the task, Darbois Texier et al. built upon a recent phenomenological model for discontinuously shear-thickening fluids proposed by Wyart & Cates (2014). In this model, a suspension like cornstarch is able to abruptly increase its viscosity at a critical stress or shear rate. The microstructural origin of this effect is that short-range repulsive forces are sufficient to hold apart the particles of the suspension at lower stresses or shear rates, resulting in a relatively low effective viscosity. But at higher stresses or shear rates, the short-range repulsion is no longer sufficient, particles abruptly jam together and the additional friction prompts a dramatic rise in viscosity (see also, for example, Brown & Jaeger 2014; Mari et al. 2015a,b; Morris 2020).

In the Wyart & Cates model, the discontinuous shear-thickening transition arises because the associated flow curve (i.e. the graph of stress against shear rate under steady, uniform shear) does not increase monotonically, but turns back to smaller shear rates at a critical point. The continuation of the flow curve back to smaller shear rates, but higher stresses, is unstable because it implies a dynamical runaway (an enhancement in flow speed being unable to counter any increase in driving force; e.g. Olmsted 2008). As noted by Darbois Texier et al., the steady flow of a uniform film down an incline corresponds to a fixed-stress problem, and should those base-flow stresses increase past the turnaround and continue on to the bent-back branch of the flow curve, the stage is set for flow instability. Darbois Texier et al. then used a thin-film approximation of the governing fluid equations, supplemented by a particular version of the Wyart & Cates model, to demonstrate that unstable waves do indeed appear. Moreover, they showed that instability was possible even without inertia.

An important result in the analysis presented by Darbois Texier et al. (2020) is that, if the steady-state Wyart & Cates model is employed to compute the local viscosity, the rheological instability along the bent-back part of the flow curve translates to an ill-posed mathematical problem in inertialess, linearized, thin-film theory: an ultraviolet catastrophe appears in the spectrum of unstable linear waves, and no preferred wavelength is predicted (despite what look to be well-defined wave spacings in experiments). In fact, generalizations of models like that of Wyart & Cates model have already been proposed to incorporate the time-dependent relaxation of the structure responsible for shear thickening (e.g. Nakanishi & Mitarai 2011; Mari et al. 2015b; Chacko et al. 2018; Richards et al. 2019). Darbois Texier et al. included such a generalization in their analysis of unstable waves on falling inertial films, to assist with their comparison with experiments. This raises the question as to whether time-dependent relaxation can regularize the thin-film instability and furnish preferred wavelengths, much like the effect of thermal relaxation on the thermo-viscous instabilities of shallow ice flows (Clarke, Nitsan & Paterson 1977; Hindmarsh 2004).

The purpose of the present article is to continue along the vein of Darbois Texier et al.'s theoretical approach and provide an asymptotic analysis of the problem, incorporating the time-dependent relaxation of frictional contacts. We also allow for spatial diffusion of those contacts with similar considerations of regularization in mind. The analysis provided by Darbois Texier et al. (2023) actually included inertia in addition to relaxation, leading them to follow the standard procedure of vertical averaging to derive thin-film equations. However, the most straightforward of such approximations are not asymptotic in the fashion in which they deal with inertia. As a consequence (and already noted by Darbois Texier et al.), such vertically averaged models are known to give inaccurate results for stability thresholds for roll waves in Newtonian (Chang, Demekhin & Kopelevich 1993; Ruyer-Quil & Manneville 2000) and non-Newtonian films (Balmforth & Liu 2004). It is also not clear how accurately vertical averaging treats the time-dependent relaxation and diffusion of contacts. Consequently, after reformulating the thin-film model in § 2, we first revisit the stability problem and derive asymptotic stability thresholds without inertia in § 3. Some special limits of the problem are considered in § 4 and § 5, allowing us to compare with Darbois Texier et al.'s earlier results and establish the impact on linear stability of either rapid relaxation or strong diffusion (relative to advection). In § 6, we then advance beyond linear stability theory and provide an exploration of the nonlinear wave dynamics in order to uncover the fate of linear instabilities once they reach finite amplitude. Finally, we conclude in § 7 with a discussion of our results and their implications for experiments with flowing films of cornstarch suspensions.

2. Shallow flow model

2.1. Dimensional formulation

Consider the flow of a complex fluid over a plane that is inclined at an angle $\theta$. The geometry is described by a Cartesian coordinate system $({\hat {x}},{\hat {z}})$, orientated such that the $x$-axis points downslope; see figure 1. The fluid velocity is $\boldsymbol {{\hat {u}}} = ({\hat {u}},{\hat {w}})$. The local fluid depth is ${\hat {z}} = {\hat {h}}({\hat {x}},{\hat {t}})$. We take the slope angle $\theta$ to be small and define

(2.1)\begin{equation} \varepsilon = \tan\theta \ll 1. \end{equation}

The fluid is also shallow, with a mean depth ${\mathcal {H}}$ that is much smaller than the characteristic length scale for variations over the plane, ${\mathcal {L}}$. In particular, we choose the length scale ${\mathcal {L}}$ so that ${\mathcal {H}}/{\mathcal {L}} = \varepsilon$, and then consider waves in spatially periodic domains of length of $2{\rm \pi} {\mathcal {L}}/k$, where $k$ is an $O(1)$ dimensionless wavenumber. Given these choices, the dimensional wavelength is $2{\rm \pi} {\mathcal {L}}/k \equiv 2{\rm \pi} {\mathcal {H}}/(k\tan \theta )$, which is much larger than the mean depth if $2{\rm \pi} \gg \varepsilon k = k\tan \theta$.

Figure 1. A sketch of the model geometry. The complex fluid has depth $h(x,t)$ and a frictional contact density described by a spatially varying order parameter $\lambda (x,z,t)$ (represented by the colour map).

Assuming that the fluid is incompressible and inertia is negligible, conservation of mass and momentum demand that

(2.2)\begin{equation} \frac{\partial{{\hat{u}}}}{\partial{{\hat{x}}}} + \frac{\partial{{\hat{w}}}}{\partial{{\hat{z}}}} = 0 \end{equation}

and

(2.3)\begin{equation} \boldsymbol{0} = \rho {\boldsymbol{g}} - \boldsymbol{\nabla} {\hat{p}} + \boldsymbol{\nabla} \boldsymbol{\cdot} \hat{\boldsymbol{\tau}}, \end{equation}

where ${\hat {p}}$ is the pressure, $\rho$ is the density, and ${\boldsymbol {g}} = (g \sin {\theta }, 0, -g \cos {\theta })$, with constant gravitational acceleration $g$ (we use the hat notation to denote dimensional variables; this decoration is removed below using suitable scalings to arrive at our dimensionless model). We take the deviatoric stress $\boldsymbol {{\hat {\tau }}}=\{{\hat {\tau }}_{ij}\}$ to be related to the rate of strains by the generalized Newtonian fluid model

(2.4)\begin{equation} {\hat{\tau}}_{ij} = {\hat{\mu}}(\lambda) \hat{\dot{\gamma}}_{ij} , \end{equation}

where

(2.5)\begin{equation} \hat{\dot{\boldsymbol{\gamma}}} = \{\hat{\dot{\gamma}}_{ij}\} = \boldsymbol{\nabla} \hat{\boldsymbol{u}} + (\boldsymbol{\nabla} \hat{\boldsymbol{u}})^{\rm T} , \end{equation}

and the second invariants of the tensors are $\hat {\dot {\gamma }} = \sqrt {\frac 12\hat {\dot {\gamma }}_{ij}\hat {\dot {\gamma }}_{ij}}$ and ${\hat {\tau }} = \sqrt {\frac 12{\hat {\tau }}_{ij}{\hat {\tau }}_{ij}}$. The viscosity ${\hat {\mu }}(\lambda )$, is controlled by the parameter $\lambda ({\hat {x}},{\hat {z}},{\hat {t}})$.

At ${\hat {z}}=0$ we adopt the no-slip condition. At the top surface ${\hat {z}}={\hat {h}}({\hat {x}},{\hat {t}})$, we ignore surface tension (in view of the relatively large scale of the films and waves featuring in experiments; see § 2.5), and adopt stress-free conditions. Thus

(2.6a,b)\begin{equation} \boldsymbol{{\hat{u}}} = 0 \quad \text{at}\ {\hat{z}} = 0, \quad ({\hat{\tau}}_{ij} - {\hat{p}} \delta_{ij})n_j = 0 \quad \text{at}\ {\hat{z}} = {\hat{h}}({\hat{x}},{\hat{t}}), \end{equation}

where $\boldsymbol {n}$ is the normal to the surface ${\hat {z}} = {\hat {h}}$. The kinematic condition implies

(2.7)\begin{equation} \frac{\partial{{\hat{h}}}}{\partial{{\hat{t}}}} + {\hat{u}} \frac{\partial{{\hat{h}}}}{\partial{{\hat{x}}}} = {\hat{w}} \quad \text{at} \ {\hat{z}} = {\hat{h}}({\hat{x}},{\hat{t}}). \end{equation}

2.2. Dimensionless leading-order formulation

To remove the dimensions from the equations, we introduce the scalings

(2.8a–c)$$\begin{gather} {\hat{t}} = \frac{{\mathcal{L}}}{{\mathcal{U}}}t,\quad {\hat{x}} = {\mathcal{L}} x, \quad ({\hat{z}},{\hat{h}}) = {\mathcal{H}}(z,h), \end{gather}$$

(2.9a–e)$$\begin{gather}{\hat{u}} = {\mathcal{U}} u, \quad {\hat{w}}=\varepsilon {\mathcal{U}} w,\quad {\hat{p}} = \rho g {\mathcal{H}} p \cos{\theta}, \quad {\hat{\tau}}_{ij} = \frac{\mu _{o} {\mathcal{U}}}{{\mathcal{H}}}\tau_{ij}, \quad {\hat{\mu}} = \mu _{o} \mu, \end{gather}$$

where $\mu _{o}$ is a characteristic viscosity, and

(2.10)\begin{equation} {\mathcal{U}} = \frac{{\mathcal{H}}^3 \rho g}{{\mathcal{L}} \mu _{o}} \cos{\theta}.\end{equation}

With these scalings, and to leading order in $\varepsilon$, (2.3) reduces to the lubrication equations

(2.11a,b)\begin{equation} 0 = 1 - \frac{\partial{p}}{\partial{x}} + \frac{\partial{\tau_{xz}}}{\partial{z}} ,\quad 0 ={-}1 -\frac{\partial{p}}{\partial{z}}. \end{equation}

The dominant component of the rate of strain tensor is $\dot {\gamma }_{xz} = \partial u/\partial z+O(\varepsilon ^2)$. Therefore, to leading order, the stress conditions in (2.5b) become

(2.12)\begin{equation} p= \tau_{xz} = 0 \quad \text{at} \ z=h(x,t). \end{equation}

The kinematic condition (2.7) is unchanged after scaling, but for the removal of the hats.

Equations (2.11) and (2.12) imply that the pressure is hydrostatic

(2.13)\begin{equation} p = h - z, \end{equation}

and the shear stress is given by

(2.14)\begin{align} \tau_{xz} &= (h-z)\left(1-\frac{\partial h}{\partial x}\right) \nonumber\\ &= \mu(\lambda)\frac{\partial u}{\partial z}. \end{align}

We write the shear stress in terms of its basal value

(2.15)\begin{equation} \tau_{xz} = (1-\zeta) \tau_b, \quad \tau_b = h \left(1-\frac{\partial h}{\partial x}\right) , \ \zeta = \frac{z}{h} .\end{equation}

In the shallow limit, the tensor invariants become approximated by $\tau \approx |\tau _{xz}|$ and $\dot \gamma \approx |\dot \gamma _{xz}| \approx |\partial u / \partial z|$.

Finally, mass conservation integrated over the fluid layer implies

(2.16)\begin{equation} \frac{\partial{h}}{\partial{t}} + \frac{\partial{}}{\partial{x}}\int_0^h u \,{\rm d} z = \frac{\partial{h}}{\partial{t}} + \frac{\partial{}}{\partial{x}}\int_0^h(h-z)\frac{\partial{u}}{\partial{z}}\,{\rm d} z= 0. \end{equation}

Given

(2.17)\begin{equation} \frac{\partial{u}}{\partial{z}} \approx \dot\gamma = \frac{\tau}{\mu}, \end{equation}

we may substitute the relevant constitutive law into the final integral in (2.16) to arrive an evolution equation for the fluid thickness. Unfortunately, this reduction is complicated by the order parameter $\lambda$ which, in general, retains an unknown spatial profile and satisfies its own evolution equation, as discussed below.

2.3. Constitutive model

In Darbois Texier et al.'s formulation of the Wyart & Cates's model, the order parameter $\lambda (x,z,t)$ is identified as the local density of frictional contacts. In steady uniform shear, this density is dictated by the local shear stress: $\lambda = {\rm e}^{-\tau _*/\tau }$, where $\tau _*$ represents the characteristic stress for which short-range repulsion can be breached. Following earlier work (Chacko et al. 2018; Richards et al. 2019; Darbois Texier et al. 2023), we allow for both relaxation and diffusion of the frictional contacts by replacing the steady uniform shear relation by the evolution equation

(2.18)\begin{equation} \frac{\partial{\lambda}}{\partial{{\hat{t}}}}+ {\hat{u}}\frac{\partial{\lambda}}{\partial{{\hat{x}}}}+ {\hat{w}}\frac{\partial{\lambda}}{\partial{{\hat{z}}}} = \beta \dot\gamma \left[\exp\left(-\frac{\tau_*}{{\hat{\tau}}}\right) - \lambda\right] + K \nabla^2 \lambda , \end{equation}

where the relaxation rate is dictated by a multiple $\beta$ of the local shear rate, and the diffusivity is $K$. The fluid rheology is then set by the viscosity law

(2.19) \begin{equation} \left.\begin{array}{ll@{}} {\hat{\tau}} = {\hat{\mu}} \hat{\dot{\gamma}}, \quad {\hat{\mu}} = {\mu _{o}\lambda_{o}^2}{({\lambda_{_O}} - \lambda )^{{-}2}}, & \lambda < {\lambda_{_O}}, \\ \hat{\dot{\gamma}} = 0, & \lambda = {\lambda_{_O}}, \end{array}\right\} \end{equation}

where the characteristic viscosity $\mu _{o}$ is related to the solvent viscosity constant $\eta _s$ defined by Darbois Texier et al. by

(2.20)\begin{equation} \mu _{o}= \frac{\eta_s}{(\phi_0-\phi)^2} . \end{equation}

In the model proposed by Wyart & Cates (2014), the jamming fraction ${\lambda _{_O}}$ is determined with reference to solid fraction $\phi$ and two other parameters

(2.21)\begin{equation} {\lambda_{_O}} = \frac{\phi_0 - \phi}{\phi_0-\phi_1} , \end{equation}

where $\phi _0$ and $\phi _1$ are the jamming fractions for suspensions of frictionless and frictional particles, respectively. However, for the constitutive relation (2.19), all we require is the parameter ${\lambda _{_O}}$, in addition to the characteristic viscosity $\mu _{o}$.

Scaling as in § 2, we arrive at the (leading-order) dimensionless constitutive model for a thin film

(2.22)\begin{equation} {\mathcal{T}} \left( \frac{\partial{\lambda}}{\partial{t}}+ u\frac{\partial{\lambda}}{\partial{x}}+ w\frac{\partial{\lambda}}{\partial{z}} \right) = {\dot{\gamma}} \left[\exp\left(-\frac{\varUpsilon}{\tau}\right) - \lambda\right] + \kappa \frac{\partial^2\lambda}{\partial z^2} , \end{equation}

and

(2.23)\begin{equation} {\dot{\gamma}} = \tau \max\left(0, 1 - \frac{\lambda}{{\lambda_{_O}}}\right)^2 , \end{equation}

where the switch in (2.23) takes care of the yield condition implied by (2.19). Here, in order to ensure that the model combines time-dependent relaxation and vertical diffusion with the breaching of short-range repulsion, we have assumed that the following dimensionless groups are all order one:

(2.24a–c)\begin{equation} {\mathcal{T}} = \frac{\varepsilon}{\beta} = \frac{{\mathcal{H}}}{{\mathcal{L}}\beta}, \quad \varUpsilon = \frac{{\mathcal{H}}\tau_*}{\mu _{o}{\mathcal{U}}} = \frac{\tau_*}{\rho g {\mathcal{H}} \tan\theta} , \quad \kappa = \frac{K}{\beta{\mathcal{U}}{\mathcal{H}}} . \end{equation}

In other words, the model corresponds to a particular distinguished limit of the physical parameters of the problem, and shares common points with other models used for thixotropic fluids (e.g. Mewis & Wagner 2009; Hewitt & Balmforth 2013; Larson & Wei 2019). The thin-film theory that combines the constitutive law in (2.22)–(2.23) with (2.16) is similar to shallow ice models that explore thermo-viscous instabilities in glaciers (e.g. Clarke et al. 1977; Hindmarsh 2004).

The introduction of the diffusion term demands the addition of further boundary conditions for $\lambda (x,z,t)$. We adopt the no-flux conditions

(2.25)\begin{equation} \frac{\partial{\lambda}}{\partial{z}} = 0 \quad {\rm at} \ z=0 \ \& \ z=h, \end{equation}

corresponding to the physical statement that frictional contacts between particles are neither created nor eliminated at the fluid surfaces. One might imagine that interfacial interactions could adjust contact densities locally, but without any further physical input, the no-flux condition seems least divisive.

2.4. The flow curve

The flow curve of a model fluid corresponds to the manner in which the shear stress $\tau$ depends on shear rate ${\dot {\gamma }}$, under conditions of steady uniform shear. For the current constitutive law, the inverse of the flow curve can be expressed as

(2.26)\begin{equation} \dot\gamma = \tau \left[ 1 - {\lambda_{_O}}^{{-}1} \exp\left(-\frac{\varUpsilon}{\tau}\right) \right]^2 , \end{equation}

which is illustrated for a range of values of ${\lambda _{_O}}$ (and $\varUpsilon =\frac 12$) in figure 2. At lower volume fractions, or higher values of ${\lambda _{_O}}$ (redder curves), the flow curve is monotonic; the viscosity increases smoothly with ${\dot {\gamma }}$, displaying a modest amount of continuous shear thickening. By contrast, at higher volume fraction, or lower ${\lambda _{_O}}$ (bluer curves), the flow curve bends back on itself at higher stresses to create distinctive non-monotonic stress–strain-rate curves. The criterion for the flow curve to fold back on itself is ${\lambda _{_O}}<2\textrm {e}^{-1/2}\approx 1.2131$. When this condition is met, the branches of the flow curve with negative slope are interpreted to be unstable, and any increase in shear rate past the turn back of the curve must prompt sudden, or discontinuous shear thickening. Such behaviour sets the scene for wave formation on inertialess films (Darbois Texier et al. 2020, 2023).

Figure 2. Flow curves in steady uniform shear for $\varUpsilon =\frac 12$ and ${\lambda _{_O}}=0.4$, $0.75$, $0.95$, 1, $1.02$, $1.05$, $1.15$, $1.35$ and $2$ (increasing from blue to red, or as indicated by the arrow).

When $1<{\lambda _{_O}}<2\textrm {e}^{-1/2}$, the folded back part of the flow curve eventually reaches a second fold point and then turns back to return to higher shear rate. The flow curve then adopts a characteristic S-shape with multiple stable branches over a range of shear rates. For ${\lambda _{_O}}<1$, however, the bent-back flow curve meets the yield point, ${\dot {\gamma }}=0$ and $\tau =\tau _{Y}=-\varUpsilon /\ln {\lambda _{_O}}$, without turning at a second fold point; for $\tau <\tau _{Y}$ the material does not deform.

Darbois Texier et al. (2023) fit the flow curve in (2.26) to rheometer measurements of the suspensions that they use for flowing cornstarch experiments. Those fits work well when the shear thickening is continuous (${\lambda _{_O}}>2\textrm {e}^{-1/2}$), or up to the first turnaround of the flow curve when thickening is discontinuous (${\lambda _{_O}}<2\textrm {e}^{-1/2}$). The bent-back portion of the flow curve is not calibrated in their rheometry, and no upper branch of an S-shaped curve was reliably found. Indeed, there is some controversy in the recent literature on discontinuous shear thickening as to whether a fluid-like upper branch even exists (Mari et al. 2015b; Morris 2020). Caution should therefore be exercised in adopting constitutive models like (2.22)–(2.23), particularly at higher stress levels. Here, we press on with the model in order to examine more closely its predictions for the dynamics of inertialess thin films, noting only that the stress levels attained never reach much beyond the first turnaround of the flow curve.

Note that the dimensionless model reduces to a Newtonian flow law by taking the limit, ${\lambda _{_O}}\to \infty$. The flow curve also becomes Newtonian when $(\varUpsilon /\tau )\to \infty$ or $(\varUpsilon /\tau )\to 0$, although the two limits have a different effective viscosity. Nevertheless, unless both ${\mathcal {T}}$ and $\kappa$ also vanish, frictional contacts can still evolve in those two limits leading to time-dependent rheology.

2.5. Parameter settings

In addition to the dimensionless diffusivity $\kappa$, the model in (2.15), (2.16), (2.22) and (2.23) contains three dimensionless rheological parameters, $\varUpsilon$, ${\mathcal {T}}$ and ${\lambda _{_O}}$. These parameters correspond to the stress needed for frictional contact, the relaxation time and the jamming threshold, respectively. In view of the definitions (2.21) and (2.24), suspensions prepared with varying solid fraction $\phi$ possess different values for ${\lambda _{_O}}$, but the same $\varUpsilon$ and ${\mathcal {T}}$.

Based on their rheometry, Darbois Texier et al. (2023) quote $\phi _0=0.52$, $\phi _1=0.43$, $\eta _s=9.1\times 10^{-4}$ Pa s and $\tau _*=12$ Pa, using a range of solid fractions $0.3\leq \phi \leq 0.47$. Their film experiments have mean depths of 1 cm or less. Such values imply that the parameter ${\lambda _{_O}}$ lies over the range 0.56–2.44, and $\varUpsilon \approx \frac 12$, which guide our parameter choices in figure 2 and hereon. For the relaxation time, Darbois Texier et al. did not measure any particular value, but quote estimates for frictional spheres from previous work (Chacko et al. 2018; Richards et al. 2019) of $\beta =10-10^{2}$, translating to dimensionless relaxation times of order $10^{-2}-10^{-3}$. As we shall see below in § 4, small values of ${\mathcal {T}}$ are problematic in the thin-film model (the distinguished limit taken in that model, in which ${\mathcal {T}}$ is taken to be order one, is also called into question, although one must simply set ${\mathcal {T}}=0$ when $\beta \gg \varepsilon$). In view of this, and the lack of any calibration, we leave open the choice for this parameter, along with that for $\kappa$. This dimensionless diffusivity is introduced chiefly so that vertical diffusion may assist in curing any mathematical problems in our thin-film theory, not necessarily as the gauge of a real physical effect. For that reason, we monitor the effect of varying this parameter, but mostly treat it as small.

3. Equilibria and linear stability

3.1. Base states

Solutions with the form of a steady sheet flow are given by

(3.1a–c)\begin{equation} u=U(z), \quad \lambda = \varLambda(z), \quad \tau=1-z, \end{equation}

where the profiles $U(z)$ and $\varLambda (z)$ follow from

(3.2a,b)\begin{equation} U_z = (1-z) \max\left(0,1-\frac{\varLambda}{{\lambda_{_O}}}\right)^2, \quad \varLambda_{zz} = \frac{U_z}{\kappa} [{\rm e}^{-\varUpsilon/(1-z)} - \varLambda], \end{equation}

with $U(0)=\varLambda _z(0)=\varLambda _z(1)=0$. Sample solutions to the prescribed-stress problem in (3.1) are displayed in figure 3. Examples with four values ${\lambda _{_O}}$ are presented, taking $\varUpsilon =\frac 12$, and diffusion constants of $\kappa =3\times 10^{-4}$ or $\kappa =0$. Because the stress $\tau =1-z$ increases monotonically on descending through the fluid layer, shear thickening occurs primarily near the underlying plane, and becomes most pronounced for the lowest values of ${\lambda _{_O}}$ (highest solid fractions).

Figure 3. (a) Flow profile, $U(z)$, and (b) order parameter, $\varLambda (z)$, for steady uniform films with $\varUpsilon =\frac 12$, $\kappa =3\times 10^{-4}$ and ${\lambda _{_O}}=0.4$, $0.75$, 1 and $1.35$ (all solid blue). The (red) dashed lines show the solutions with $\kappa =0$. The inset replots the solutions on the $({\dot {\gamma }},\tau )$-plane and compares them with the steady-shear flow curves. The square for ${\lambda _{_O}}=0.4$ and $\kappa =0$ indicates the yield surface where $\varLambda ={\lambda _{_O}}$.

For ${\lambda _{_O}}\gg 1$, the flow profile limits to the Nusselt profile, $U=z-\frac 12 z^2$, of a Newtonian fluid. With $\kappa =0$, on the other hand, we find the explicit solution

(3.3a,b) \begin{align} U(z) = \int_0^z (1-\tilde{z}) \left[ {\rm max} \left(0, 1 - \lambda_{_O}^{-1} {\rm e}^{-\varUpsilon/(1-z)} \right) \right]^2 \,{\rm d}\tilde{z} ,\quad \varLambda(z) = \min({\lambda_{_O}}, {\rm e}^{-\varUpsilon/(1-z)}). \end{align}

The numerically computed solutions for $\kappa =3\times 10^{-4}$ closely track this diffusionless solution in figure 3, except near the top and lower surfaces, where the no-flux condition exerts an effect, and for the case with ${\lambda _{_O}}=0.4$. For that lowest value of ${\lambda _{_O}}$, the diffusionless order parameter reaches the limit ${\lambda _{_O}}$ at a point within the fluid layer. This results in a yield surface below which material jams up and becomes rigid. With diffusion, however, $\varLambda (z)$ becomes smoothed and never reaches the yield point. When translated to loci on the $({\dot {\gamma }},\tau )$-plane (as in the inset to figure 3), the diffusionless solutions trace out part of the flow curve; the paths taken by the solutions with $\kappa =3\times 10^{-4}$ follow a similar vein.

For higher diffusivities $\kappa$, the order parameter becomes more significantly smoothed, reducing the spatial viscosity variation and lifting the portraits of the solutions on the $({\dot {\gamma }},\tau )$-plane away from the flow curves; see figure 4. Near $\kappa =0.02$, the smoothing removes any fold back of the stress–strain-rate curves, and for $\kappa >1$, diffusion becomes sufficient to render $\varLambda$ almost uniform across the film (given the no-flux boundary conditions). A Newtonian-like, strong-diffusion solution then emerges with

(3.4a,b)\begin{equation} U\sim \left(z-\frac{1}{2} z^2\right) \max\left(0,1-\frac{\varLambda}{{\lambda_{_O}}}\right)^2, \quad \varLambda\sim 2\int_0^1 (1-z)\,{\rm e}^{-\varUpsilon/(1-z)}\,{\rm d} z . \end{equation}

Note that (3.1) predicts that the limiting order parameter $\varLambda$ exceeds ${\lambda _{_O}}$ for ${\lambda _{_O}}<0.44321$, implying that the entire layer plugs up with sufficient diffusion.

Figure 4. (a) Flow profile, $U(z)$, (b) $\varLambda (z)$, and (c) portraits on the $({\dot {\gamma }},\tau )$-plane for steady uniform film solutions with $\varUpsilon =\frac 12$ and three values of ${\lambda _{_O}}$ and $\kappa$ (as indicated, and colour coded by $\kappa$). The dashed (green) lines show the limits for $\kappa \gg 1$.

3.2. Linear stability analysis

Infinitesimal perturbations to the base states above, with

(3.5a–c)\begin{equation} h = 1+{\check\eta} \,{\rm e}^{{\rm i}kx+\sigma t}, \quad u = U(z)+\psi_z(z) \,{\rm e}^{{\rm i}kx+\sigma t}, \quad \lambda = \varLambda(z)+{\check\lambda}(z) \,{\rm e}^{{\rm i}kx+\sigma t}, \end{equation}

wavenumber $k$ and (complex) growth rate $\sigma =\sigma _r+i\sigma _i$, satisfy

(3.6)$$\begin{gather} [\sigma + {\rm i}k U(1)] {\check\eta} ={-}{\rm i}k \psi(1), \end{gather}$$

(3.7)$$\begin{gather}\psi_{zz} = \left( 1 - \frac{\varLambda}{{\lambda_{_O}}}\right)^2 {\check\tau} - \frac{2}{{\lambda_{_O}}}(1-z) \left( 1 - \frac{\varLambda}{{\lambda_{_O}}}\right) {\check\lambda} , \end{gather}$$

(3.8)$$\begin{gather}{\mathcal{T}} [ (\sigma+{\rm i}kU) {\check\lambda} - {\rm i}k \varLambda_z\psi ] = \frac{\varUpsilon U_z {\check\tau} \,{\rm e}^{-\varUpsilon/(1-z)}}{(1-z)^2} + [{\rm e}^{-\varUpsilon/(1-z)} - \varLambda] \psi_{zz} - U_z {\check\lambda} + \kappa {\check\lambda}_{zz} . \end{gather}$$

Here, $\psi (z)$ represents a streamfunction such that $(u,w)=(U+\psi _z\,\textrm {e}^{\textrm {i}kx+\sigma t},-\textrm {i}k\psi \,\textrm {e}^{\textrm {i}kx+\sigma t})$, and the shear stress perturbation has amplitude

(3.9)\begin{equation} {\check\tau} = [1 - {\rm i}k(1-z)]{\check\eta}. \end{equation}

The boundary conditions translate to $\psi (0)=\psi _z(0)={\check \lambda }_z(0)={\check \lambda }_z(1)=0$.

Numerical results of the linear stability analysis are shown in figure 5, which plots the growth rate of the most unstable mode against wavenumber $k$ for $(\kappa,{\mathcal {T}},\varUpsilon )=(10^{-3},10^{-2},\frac 12)$ at several values of ${\lambda _{_O}}$. With the highest values of ${\lambda _{_O}}$ of $1.2<2\textrm {e}^{-1/2}$ and $1.35$ (the lowest solid fractions; redder curves), all modes are stable, even though the base state for the first of these values possesses an S-shaped flow curve. The lower values of ${\lambda _{_O}}$ (higher solid fractions; bluer curves) are unstable for wavenumbers below a critical cutoff $k=k_{crit}$. The growth rate is maximized at the particular wavenumber $k=k_{max}$ indicated in the plots. As illustrated in figure 5(a,b) and discussed below in § 4.1, the growth rate and phase speed for $k\to 0$ can be predicted analytically.

Figure 5. (a) Growth rate, $\sigma _r$, and (b) scaled phase speed, $-\sigma _i/(kU_*)$, against wavenumber $k$ for $(\kappa,{\mathcal {T}},\varUpsilon )=(10^{-3},10^{-2},\frac 12)$ and ${\lambda _{_O}}=\{\frac 34,\frac 78,1,1.1,1.2,1.35\}$ (from blue to red). Scaled phase speeds are shown only where $\sigma _r>-2$. The dashed line in (b) shows the prediction in (4.5) of § 4.1. The corresponding prediction for the growth rate is included in the inset of (a), which plots $\sigma _r/k^2$ for smaller wavenumber. The stars show the most unstable modes for ${\lambda _{_O}}<1.2$; the corresponding eigenfunctions, $\psi _z(z)$ and ${\check \lambda }(z)$, are shown in (c) and (d), normalized so that ${\check \eta }=1$; the real parts are shown by solid lines and the imaginary parts as dashed lines.

The most unstable modes have eigenfunctions (shown in figure 5c,d) which are characterized by strong perturbations in $\lambda$ over the lower part of the fluid layer. These variations are predominantly opposite to the perturbations in speed $\psi _z$ and surface slope $\textrm {i}k{\check \eta }$. Such features imply that a local upturn in surface slope, corresponding to a local decrease in stress, weakens $\lambda$ and thence viscosity, to accelerate flow. Conversely, a local downturn in surface slope leads to an increasing stress, the strengthening of $\lambda$ and flow deceleration. In combination, wavey perturbations become amplified. In other words, the perturbations harness a material response mirroring the fold back of the flow curve for ${\lambda _{_O}}<2\textrm {e}^{-1/2}$, as described previously by Darbois Texier et al. (2020).

Growth rates and phase speeds for varying ${\lambda _{_O}}$ and ${\mathcal {T}}$ are plotted in figure 6. The degree of instability increases continually as the relaxation time decreases, indicating a singular limit for ${\mathcal {T}}\to 0$. Conversely, the instability becomes suppressed for sufficiently large relaxation time. The onset of instability also occurs for finite wavenumber as ${\lambda _{_O}}$ decreases below $\textrm {e}^{-1/2}$, most noticeably for higher ${\mathcal {T}}$. The phase speeds, $-\sigma _i/k$, plotted in figures 5 and 6 are scaled by the mean speed (flux) of the base solutions

(3.10)\begin{equation} U_* = \int_0^1 U(z)\, {\rm d} z. \end{equation}

At very low wavenumbers, and for smaller relaxation times, instability first appears for modes with phase speeds that are roughly twice the mean flow speed. This feature is discussed further below in § 4, and was exploited by Darbois Texier et al. to rationalize experimental observations. However, the most unstable modes over all wavenumbers have rather lower phase speeds, closer to and often less than the mean flow speed.

Figure 6. (a) Growth rate, $\sigma _r$, and (b) scaled phase speed, $-\sigma _i/(kU_*)$, plotted as densities on the $(k,{\lambda _{_O}})$-plane, with $(\kappa,\varUpsilon )=(10^{-3},\frac 12)$, and ${\mathcal {T}}=10^{-3}$, $10^{-2}$, $0.1$ and $\frac 12$ (from right to left). The thicker red lines indicate the most unstable wavenumber $k_{max}$ for each ${\lambda _{_O}}$. The colour scales saturate at negative growth rates.

Growth rates as a function of $k$ and $\kappa$ at fixed ${\lambda _{_O}}=1$ and ${\mathcal {T}}=0.1$ are shown in figure 7. This plot extends from close to the diffusionless limit ($\kappa \to 0$), to the strongly diffusive limit ($\kappa \gg 1$). The stability problem simplifies somewhat in the first of these limits because ${\check \lambda }$ becomes determines algebraically from $\psi$ and ${\check \tau }$ in (3.8) (bearing in mind that $\varLambda \to \textrm {e}^{-\varUpsilon /(1-z)}$ for $\kappa \to 0$), and one must solve only (3.7). Further discussion of the opposite limit of strong diffusion is given below in § 5. Unexpectedly, perhaps, instability persists in this latter limit, extending to increasingly high wavenumbers as $\kappa$ is raised. In other words, the diffusion of frictional contacts does not suppress instability, even though a sufficient increase in $\kappa$ eliminates any turn back in the local $({\dot {\gamma }},\tau )$-relation of the base state (see figure 4).

Figure 7. Density plots of (a) growth rate, $\sigma _r$, and (b) scaled phase speed, $-\sigma _i/(kU_*)$ above the $(k,\kappa )$-plane for unstable modes with $({\lambda _{_O}},{\mathcal {T}},\varUpsilon )=(1,0.1,\frac 12)$. The thicker red line indicates the most unstable wavenumber $k_{max}$ for each $\kappa$. The colour scales saturate at negative growth rates. Below are plots of (c,e) $\sigma _r$, and (d,f) $-\sigma _i/(kU_*)$ against $k$ for the values of $\kappa$ indicated. The dashed lines show the limits $\kappa \to \infty$ (see § 5) and $\kappa \to 0$.

4. Rapid relaxation, ${\mathcal {T}}\ll 1$

With a relatively rapid relaxation of the frictional contacts (${\mathcal {T}}\to 0$), the order parameter becomes determined by solving

(4.1)\begin{equation} {\check\kappa} \lambda_{\zeta\zeta} = (1-\zeta) \left(1 - \frac{\lambda}{{\lambda_{_O}}}\right)^2 [\lambda - {\rm e}^{-{\check\Upsilon}/(1-\zeta)}], \end{equation}

with

(4.2a–e)\begin{equation} \tau_b = h(1-h_x),\quad \zeta=\frac{z}{h},\quad {\check\Upsilon} = \frac{\varUpsilon}{\tau_b}, \quad {\check\kappa} = \frac{\kappa}{h^2\tau_b}, \quad \lambda_\zeta(0)=\lambda_\zeta(1)=0, \end{equation}

on assuming the yield condition is never met. This problem, however, is identical to that for the base states in § 3.1, but for the replacements $\kappa \to {\check \kappa }$ and $\varUpsilon \to {\check \Upsilon }$. Hence, we may write the solutions to both problems in terms of a single function, as either $\lambda = \varLambda (\zeta ; \varUpsilon,\kappa )$ or $\lambda = \varLambda (\zeta ; {\check \Upsilon },{\check \kappa })$.

Of particular importance is the flux function

(4.3)\begin{align} \int_0^h u(x,z,t)\, {\rm d} z &=\int_0^1 (h-z) u_z \, {\rm d} z \nonumber\\ &= h^2\tau_b \int_0^1 (1-\zeta)^2 \left(1 - \frac{\lambda}{{\lambda_{_O}}}\right)^2 {\rm d}\zeta = h^2 \tau_b {\mathcal{Q}}({\check\Upsilon},{\check\kappa}) . \end{align}

Armed with this flux function, we may now turn to the conservation of mass relation (2.16) and write the single evolution equation

(4.4)\begin{equation} h_t + \left[h^3(1-h_x) {\mathcal{Q}}\left(\frac{\varUpsilon}{h(1-h_x)},\frac{\kappa}{h^3(1-h_x)}\right) \right]_x = 0. \end{equation}

Note that the base states of § 3.1 have a flux, or mean velocity, of $U_* = {\mathcal {Q}}(\varUpsilon,\kappa )$.

4.1. Revisiting linear stability

By introducing $h=1+{\check \eta } \,\textrm {e}^{-\textrm {i}kx+\sigma t}$ into (4.4) and linearizing, we arrive at

(4.5)\begin{equation} \sigma ={-}{\rm i}k (3U_*-\varUpsilon {\mathcal{Q}}_1-3\kappa {\mathcal{Q}}_2) + k^2 (\varUpsilon {\mathcal{Q}}_1 +\kappa {\mathcal{Q}}_2 - U_*), \end{equation}

where

(4.6a,b)\begin{equation} {\mathcal{Q}}_1 = \left[ \frac{\partial{{\mathcal{Q}}}}{\partial{{\check\Upsilon}}} \right]_{h=1} \quad {\rm and} \quad {\mathcal{Q}}_2 = \left[ \frac{\partial{{\mathcal{Q}}}}{\partial{{\check\kappa}}} \right]_{h=1}, \end{equation}

are the partial derivatives of the flux function evaluated for the base state. As long as $\varUpsilon {\mathcal {Q}}_1 +\kappa {\mathcal {Q}}_2 > U_*$, the base state is therefore unstable. The growth rate and phase speed predicted by (4.5) are included in figure 5. These predictions match up with the numerical solutions for $k\ll 1$ in these figures because relaxation is relatively rapid in the small-wavenumber limit.

For higher wavenumber, the predictions from (4.5) fail to match the drop off in linear instability observed for the numerical solutions in figure 5. In fact, (4.5) predicts an unbounded increase in growth rate with wavenumber, the hallmarks of an ultraviolet catastrophe. In other words, in the limit of rapid relaxation, the linear thin-film problem becomes ill posed with the shortest wavenumbers growing fastest. As illustrated by the numerical solutions of the linear stability problem in figures 5 and 6, this drawback is cured by a finite relaxation time. However, the approach to the singular limit ${\mathcal {T}}\to 0$ is evident in figure 6, where the range of unstable wavenumbers and maximum growth rate diverge as the relaxation time is decreased.

4.2. No diffusion

With $\kappa =0$, the calculation of the flux function becomes simpler. In this case, $\varLambda =\textrm {e}^{-{\check \Upsilon }/(1-\zeta )}$ and

(4.7)\begin{equation} G(\tau_b) = \tau_b {\mathcal{Q}}({\check\Upsilon},{\check\kappa}) = \tau_b \int_0^1 (1-\zeta)^2 \left(1 - \frac{\lambda}{{\lambda_{_O}}}\right)^2 {\rm d}\zeta \equiv \frac{1}{\tau_b^2} \int_0^{\tau_b} {\tilde\tau} \varGamma({\tilde\tau})\,{\rm d}{\tilde\tau} , \end{equation}

where $\varGamma (\tau )=\tau (1-{\lambda _{_O}}^{-1}\,\textrm {e}^{-\varUpsilon /\tau })^2$ is the inverse of the flow curve function (cf. (2.26)), which can be written in terms of exponential integrals.

The lubrication model now becomes

(4.8)\begin{equation} h_t + [h^2 G(\tau_b)]_x = 0 , \end{equation}

so that the linear growth rate can be read off as

(4.9)\begin{equation} \sigma ={-}{\rm i}k [2G(1)+G'(1)] - k^2 G'(1) . \end{equation}

Linear instability arises for

(4.10)\begin{equation} G'(1) = \int_0^1 {\tilde\tau}^2 \varGamma'({\tilde\tau}) \,{\rm d}{\tilde\tau}<0 , \end{equation}

which is equivalent to the instability condition quoted by Darbois Texier et al. The condition does not quite match the criterion, $\varGamma '(1)<0$, which indicates when the fluid at the bottom of the layer in the base flow lies beyond the first turnaround of the flow curve (although it is an integral average of $\varGamma '(\tau )$ that is weighted to the base of the fluid layer). Flux functions $G(\tau _b)$ for the same values of ${\lambda _{_O}}$ and $\varUpsilon$ as displayed in figure 2 are illustrated in figure 8; an inset compares the stability indicator $G'(1)$ with $\varGamma '(1)$. Note that $G'(1)$ is numerically small, which is the origin of Darbois Texier et al.'s conclusion that the phase speeds of unstable waves are close to twice the mean flow speed (here $2G(1)\equiv 2U_*$).

Figure 8. The flux function $G(\tau _b)$ defined in (4.7) for $\varUpsilon =\frac 12$ and the values of ${\lambda _{_O}}$ shown in figure 2. The inset compares $G'(1)$ with $\varGamma '(1)$ as a function of ${\lambda _{_O}}$.

To summarize, without a finite relaxation time, the linearized inertialess thin-film model is ill posed (a feature that likely carries over to the nonlinear versions in (4.4) and (4.8)). One might imagine that relaxing the thin-film approximation or including inertia could cure this ultraviolet catastrophe. In fact, as we show in Appendix A, where we briefly advance beyond the inertialess, thin-film limit (but omit diffusion), neither of these extensions suffices; a finite relaxation time is still needed. Surface tension, which has been omitted here, offers another possible physical regularization. The inclusion of that effect modifies the base shear stress in thin-film theory so that $\tau _b = h(1-h_x+{\mathcal {S}} h_{xxx})$, where ${\mathcal {S}}$ is a suitable, dimensionless, Bond number (the hydrostatic pressure being replaced by $p = h-z - {\mathcal {S}} h_{xx}$; e.g. Chang 1994; Ruyer-Quil & Manneville 2000). With this inclusion, a repetition of the analysis above simply replaces the factor $k^2$ in (4.5) or (4.9) with $k^2+{\mathcal {S}} k^4$. The divergence of the growth rate with $k$ is therefore exacerbated by surface tension.

5. Strong diffusion, $\kappa \gg 1$

As remarked in § 3.1, when diffusion of frictional contacts is relatively strong $\kappa \gg 1$ (and the boundary conditions on $\lambda$ are no flux), $\varLambda (z)$ becomes almost uniform across the film for the base states of the linear stability analysis. In fact, this feature carries over to the full thin-film problem, which simplifies further in this limit: integrating (2.22) across the film, and then introducing the approximation $\lambda \sim \lambda (x,t)$, we find

(5.1)\begin{equation} ( h \lambda )_t + \left( \lambda \int_0^h u\,{\rm d} z \right)_x = \frac{1}{{\mathcal{T}}} \left(1 - \frac{\lambda}{{\lambda_{_O}}}\right)_+^2 \int_0^h \tau ({\rm e}^{-\varUpsilon/\tau} - \lambda)\, {\rm d} z, \end{equation}

and

(5.2)\begin{equation} V = \frac{1}{h}\int_0^h u\,{\rm d} z = \frac{1}{3} h\tau_b \left(1 - \frac{\lambda}{{\lambda_{_O}}}\right)_+^2,\end{equation}

where we have employed the short-hand notation, $\max (0,X)=(X)_+$. Hence

(5.3) \begin{equation} \left.\begin{array}{c} h_t + (hV)_x= 0, \quad \tau_b = h(1-h_x),\\ \displaystyle (h\lambda)_t + (hV\lambda)_x = \dfrac{3V}{2{\mathcal{T}}} [ E(\tau_b) - \lambda ] , \quad E(\tau_b) = \dfrac{2}{\tau_b^2} \int_0^{\tau_{b}} {\tilde\tau} \,{\rm e}^{-\varUpsilon/{\tilde\tau}} \,{\rm d} {\tilde\tau} . \end{array}\right\} \end{equation}

For a steady, uniform base state, $h(x,t)=1$ and $\lambda (x,t)=\varLambda$, we recover the order parameter in (3.1). The linear stability of these base states follows from setting $h=1+{\check \eta } \,\textrm {e}^{\textrm {i}kx+\sigma t}$ and $\lambda = \varLambda + {\check \lambda } \,\textrm {e}^{\textrm {i}kx+\sigma t}$, linearizing in the amplitudes ${\check \eta }$ and ${\check \lambda }$ and then solving a quadratic equation for the growth rate $\sigma$ stemming from (5.3). Sample results are plotted in figure 9 for $({\mathcal {T}},\varUpsilon )=(0.1,\frac 12)$. As ${\lambda _{_O}}$ is decreases through the critical value $\lambda _{_{SD}}(\varUpsilon )=4\textrm {e}^{-\varUpsilon }-3\varLambda <2\textrm {e}^{-1/2}$ (with $\lambda _{_{SD}}(\frac 12)\approx 1.0965$), instability sets in at the largest wavenumbers. An ultraviolet catastrophe is avoided, however, and

(5.4)\begin{equation} \sigma_r \to \frac{(\lambda_{_{SD}}-{\lambda_{_O}})({\lambda_{_O}}-\varLambda)} {2{\mathcal{T}}{\lambda_{_O}}^2} \quad {\rm and} \quad -\frac{\sigma_i}{kU_*} \to 1 \quad {\rm for} \ k\gg1 . \end{equation}

For ${\lambda _{_O}}$ further below $\lambda _{_{SD}}$, all wavenumbers become unstable, but the shortest waves remain the fastest growing. The predictions for the strong-diffusion limit were also included earlier in figure 7(c,d) and compared with numerical results for the full thin-film model. Evidently, there is no selection of a preferred wavelength in linear theory and a pronounced dependence of the nonlinear dynamics on initial condition is suggested. Therefore, in the full thin-film model, a preferred wavelength arises due to the relaxation, but not diffusion, of $\lambda$.

Figure 9. (a) Growth rates $\sigma _r$ and (b) scaled phase speeds, $\sigma _i/(kU_*)$ on the $(k,{\lambda _{_O}})$-plane in the strong-diffusion limit, for $\varUpsilon =\frac 12$ and ${\mathcal {T}}=0.1$.

The simplicity of the strong-diffusion equations (5.3) suggests an avenue to interrogate the development of instabilities from low-amplitude, approximately linear perturbations into nonlinear waves. However, a device to limit the range of unstable wavenumbers is still required and the strong-diffusion limit, in which the frictional contact density becomes uniform across the depth of the fluid film, is itself probably unphysical. The exercise can nevertheless prove useful, permitting a certain amount of analytical headway into deciphering the nonlinear dynamics. In Appendix B, we follow this pathway, adding artificial diffusion-in-$x$ terms to remove instability at the highest wavenumbers. A notable feature exposed by this analysis is that the linear instability saturates at finite amplitude to form shock-like nonlinear waves, travelling at a speed that can be predicted analytically. The analysis further exposes how linear instability can extend into the limit of strong diffusion, even though the local stress–strain-rate relation of the base-flow profile is monotonic (cf. § 3.2).

6. Nonlinear waves

To provide an exploration of the nonlinear dynamics of unstable waves that avoids the strong-diffusion limit, we return to the full order parameter equation in (2.22) and capture the complete spatial dependence of $\lambda (x,z,t)$. In Appendix C, we summarize the strategy we use to solve this problem numerically for spatially periodic domains of length $2{\rm \pi} /k$, with $k$ selected close to the wavenumber that is preferred when the relaxation time ${\mathcal {T}}$ and diffusivity $\kappa$ are finite.

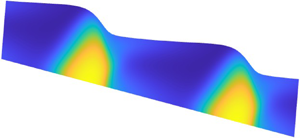
Figure 10 displays a sample numerical solution. The initially small perturbation to the base state again amplifies exponentially according to the predictions of linear stability analysis (§ 3.2). Growth then saturates in the nonlinear regime, leading to the formation of a steadily propagating wave. The nonlinear wave travels slightly more slowly than the linear wave speed, which is in turn slightly slower than the mean flow. This dynamics matches that found in the strong-diffusion limit (see Appendix B), although the nonlinear wave profile in figure 10 is relatively smooth and shows no tendency to form a shock. The fall of the profile beyond the crest does, however, become somewhat steeper than the preceding rise. Note that computations are continued only up to times just beyond where linear instability saturates; any subsequent nonlinear dynamics, such as secondary instabilities, is not captured.

Figure 10. Nonlinear solution for $({\lambda _{_O}},{\mathcal {T}},\kappa,k,A)=(1,0.1,10^{-3},10,2\times 10^{-4})$. (a) Snapshots of $\lambda (x,z,t)$ at five successive times (as indicated by the stars in (c)). The solutions are mapped onto the inclined plane. (b) The free surface position $h(x,t)$, shown in the frame of the final nonlinear wave, with spatial coordinate $\xi =k(x-c_nt)$, where $c_n\approx 0.05\approx 0.55U_*$. (c) Time series of the mean surface displacement $\sqrt {\langle (h-1)^2\rangle }$ (where $\langle \cdots \rangle$ denotes an average in $x$). The dashed line shows the growth predicted by linear stability analysis.

At early times, when the film is similar to the uniform base flow, the order parameter $\lambda (x,z,t)$ is enhanced over the lower parts of the film by the elevated shear stress there. As the nonlinear wave develops, the flattening of the surface over the rise of the wave reduces the shear stress to lower $\lambda$ locally. Shear thickening then takes place primarily underneath the fall of the wave profile, enhancing the viscosity there to create the distinctive pattern in $\lambda$ seen in the snapshots in figure 10(a).

Further details of the final, steady nonlinear wave are shown in figure 11. In the first panel, a density map of $\lambda$ is compared with contours of constant $\textrm {e}^{-\varUpsilon /|\tau |}$. Although the two are not perfectly aligned, the trends of both are similar, indicating that the local relation between $\dot \gamma$ and $\tau$ lies near, but does not follow, the steady-state flow curve. Shear thickening takes place primarily within the region where the stress exceeds the threshold, $|\tau |\approx 0.4$, implied by the first turn back of the flow curve (the black contour in figure 11a). The streamline plot in the second panel of figure 11 illustrates how the shear thickening and step conspire to create a recirculating cell underneath the crest of the nonlinear wave.

Figure 11. The final nonlinear wave from figure 10, showing (a) contours of constant $\textrm {e}^{-\varUpsilon /|\tau |}$, superposed on a density map of $\lambda$, and (b) a selection of streamlines, superposed on a density map of $u/U_*$. Both are shown in the frame of the wave, with streamwise coordinate $\xi =k(x-c_nt)$. The black curve in (a) shows the contour $|\tau |\approx 0.4$, the stress above which discontinuous shear thickening is expected (cf. figures 2 and 3).

A selection of steady nonlinear wave profiles for varying ${\lambda _{_O}}$ is shown in figure 12(a). As this parameter decreases and the linear instability becomes stronger, the wave height (measured in figure 12 as $\max (h)-\min (h)$) increases. Tracing the wave profiles back up to the onset of linear instability at larger ${\lambda _{_O}}$ suggests a supercritical transition (see panel b). At the smaller values of ${\lambda _{_O}}$, the nonlinear wave profile develops into relatively steep steps separated by long, almost linear sections. Below the steps, fluid discontinuously shear thickens throughout almost its entire depth, whereas the wave profile become almost flat between the steps, reflecting a very low shear stress. In other words, fluid gravitationally pools behind the sharp, shear-thickened steps, which implies that those features present effective barriers to the film flow.

Figure 12. (a) Steady nonlinear wave profiles for $({\mathcal {T}},k,\varUpsilon,\kappa )=(0.1,10,\frac 12,10^{-3})$ and ${\lambda _{_O}}=\{0.9,1,1.05,1.07\}$ (colour coded, from red to blue). The profiles are plotted so that their crests are aligned, and the triangle shows unit slope ($h_x=1$). (b) Wave height, $\max (h)-\min (h)$, against ${\lambda _{_O}}$, for a wider set of computations. The stars indicate the values for ${\lambda _{_O}}$ in (a,b), and the vertical dot-dashed line indicates the linear stability boundary. The inset density plots show $\lambda (x,t)$ for the values of ${\lambda _{_O}}$ indicated.

The reduction of the net flux by the nonlinear waves is illustrated further in figure 13, which displays time series of the horizontal averages of the surface and depth-averaged speed $u$ for the solutions also shown in figure 12. In all four examples, the net flow speed is reduced by the nonlinear wave, although the effect is minor near the linear stability threshold (for ${\lambda _{_O}}=1.07$). The instantaneous wave speed (measured using the position at the core of the wave where $h=1$ and $h_x<0$) is smaller still. At early times, this wave speed matches the prediction of linear theory, then falls sharply as the wave saturates, before converging to the final nonlinear wave speed $c_n< U_*$.

Figure 13. (a) Time series of three scaled speeds for $({\mathcal {T}},k,\varUpsilon,\kappa )=(0.1,10,\frac 12,10^{-3})$ and ${\lambda _{_O}}=\{0.9,1,1.05,1.07\}$ (colour coded, from red to blue). The solid line shows the depth and $x$-averaged speed, $\langle h^{-1} \int _0^h u(x,z,t) \,\textrm {d} z \rangle$, the dashed line show the $x$-averaged surface speed, $\langle u(x,h,t) \rangle$, and the dotted line show the instantaneous wave speed (measured using the position where $h=1$ and $h_x<0$). All three are scaled by $U_*$. The stars indicate the final nonlinear wave speeds, which are plotted in (b) for a wider suite of computations. The vertical dot-dashed line again shows the linear stability threshold.

7. Discussion

The non-monotonic flow curves of certain complex fluids in steady, uniform shear can trigger hydrodynamic instabilities. For suspensions that display discontinuous shear thickening such as cornstarch, this effect plausibly rationalizes the large-amplitude waves seen on relatively slow, falling films (Darbois Texier et al. 2020, 2023). Here, we have examined a detailed theoretical model of such films, building on Darbois Texier et al.'s formulation of the constitutive law for steady, uniform shear proposed by Wyart & Cates (2014). Employing that law for the local viscosity in an inertialess thin-film model is problematic: waves of all wavelength are predicted to be unstable, with a growth rate that diverges at high wavenumbers. We have demonstrated that the inclusion of both relaxation or diffusion across the film can control this ultraviolet catastrophe. On the other hand, neither inertia nor the extensional viscous stresses ignored in thin-film theory can cure the problem (a conclusion following from the extension of the thin-film model explored in Appendix A).

For the constitutive law that we have employed, relaxation removes unstable waves of small wavelength, to furnish a preferred wavenumber; diffusion, however, does not. The onset of linear instability sometimes, but not always, lies close to a long-wave stability criterion that can be established analytically. That criterion does not precisely coincide with the condition that the profile of the base flow samples the non-monotonic part of the flow curve under steady uniform shear, even in the limit that relaxation becomes arbitrarily fast. In fact, with a sufficiently long relaxation time, linear instability is suppressed altogether, even when discontinuous shear thickening arises in the base flow.

By solving the thin-film model numerically, we have constructed the steadily propagating nonlinear waves that result from the saturation of linear instability when disturbances reach finite amplitude. Changing the parameters of the constitutive law so that the rheology progresses from continuous to discontinuous shear thickening, we observe the emergence of low-amplitude waves on passing the linear instability threshold, in the usual manner of a supercritical transition. As the fluid becomes more shear thickening, the waves become stronger, taking the form of relatively steep steps, under which fluid is substantially thickened by elevated stresses. Between the steps, viscosity remains low and the fluid pools into long, almost flat, sections. Such phenomenology bears some similarities with that of the waves seen in laboratory experiments (Balmforth et al. 2005; Darbois Texier et al. 2020, 2023). However, Balmforth et al. (2005) report that waves become very steep in front of their crests, often overturning there. Darbois Texier et al. do not comment on this aspect of their experiments, although the downward profiles of their ‘Oobleck waves’ also look to quickly steepen. Excessive wave steepening and overturning cannot be captured by the thin-film asymptotics inherent in the model presented here.

Similarly, the linear stability theory predicts that preferred wavelengths are relatively short, implying further limitations on thin-film theory: in the model, the dimensional wavelength, $2{\rm \pi} k^{-1} {\mathcal {L}} = 2{\rm \pi} k^{-1} {\mathcal {H}} \cot \theta$, should greatly the fluid depth ${\mathcal {H}}$; i.e. the dimensionless wavenumber $k$ should be much less than $2{\rm \pi} \cot \theta$. For the slopes of the channels used in laboratory experiments (of order $10^\circ$), this translates to the constraint $k\ll O(30)$. Consequently, if relaxation times are relatively small, the predicted preferred wavelengths are too short to be accurately captured in the long-wave model (preferred wavenumbers are predicted to be $O(10)$ or smaller when ${\mathcal {T}}>0.1$).

The theoretically predicted linear wave speeds are also smaller than those observed experimentally by Balmforth et al. (2005) and Darbois Texier et al. (2020, 2023), who both noted that waves travelled significantly faster than the mean flow. In the model, the waves travel closer to the mean flow speed (for finite relaxation time), unless the wavenumber is arbitrarily decreased below that of the most unstable mode. Moreover, because nonlinear waves invariably create shear-thickened barriers to flow, those disturbances invariably decelerate further on reaching finite amplitude in the model. It therefore seems challenging to explain the relatively fast experimental wave speeds. One immediate explanation for this discrepancy is that the spatially periodic setting and initialization of the model lead to differences with the experiments, in which waves develop along the channel from an inlet with its own dynamics.

In conclusion, thin-film theory incorporating instantaneous shear thickening within the framework of a generalized Newtonian fluid model predicts linearly unstable waves in the inertialess limit. However, this theory is not sufficient to explain the detailed properties (wavelengths and wave speeds) of the waves observed in flowing films of cornstarch solutions. Here, it has been shown that the addition of time-dependent relaxation of frictional contacts may partly help to save this situation. Overall, the instabilities observed on flowing films of discontinuously shear-thickening fluids provide interesting constraints on the underlying constitutive behaviour, as in some other flows cornstarch suspensions (e.g. Merkt et al. 2004; von Kann et al. 2011; Brown & Jaeger 2014; Ovarlez et al. 2020; Bougouin et al. 2024). In more general settings, one wonders whether phenomena of this kind act as practical rheometers to probe and inform the rheology of complex fluids or granular media (cf. Edwards & Gray 2015).