Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T03:13:55.211Z Has data issue: false hasContentIssue false
  • English
  • Français

Instability of an inhomogeneous bacterial suspension subjected to a chemo-attractant gradient

Published online by Cambridge University Press:  17 February 2014

T. V. Kasyap  and
Donald L. Koch
T. V. Kasyap
Affiliation:
School of Chemical and Biomolecular Engineering, Cornell University, Ithaca, NY 14853, USA
Donald L. Koch*
Affiliation:
School of Chemical and Biomolecular Engineering, Cornell University, Ithaca, NY 14853, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The stability of a suspension of chemotactic bacteria confined in an infinitely long channel and subjected to a stationary, linear chemo-attractant gradient is investigated. While swimming, individual bacteria exert force dipoles on the fluid, which at the continuum level lead to a stress depending upon the bacterial orientation and number density fields. The presence of the attractant gradient causes bacteria to tumble less frequently when swimming along the gradient, leading to a mean orientation and a non-zero chemotactic drift velocity 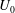$U_0$ in that direction. At long length and time scales compared to those associated with the persistence of bacterial swimming, fluxes due to chemotaxis and the random run–tumble motion of bacteria balance to yield an exponentially varying number density profile across the channel in the base state. The associated bacterial stress field is also exponentially varying and is normal. This spatially non-uniform base state is unstable to fluctuations in the bacterial concentration field when the scaled bacterial concentration 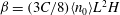$\beta = (3 C/8) \langle n_0\rangle L^2 H$ exceeds a critical value determined by a Péclet number defined as 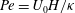${\mathit{Pe}} = U_0 H/\kappa $. Here, 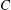$C$ is a non-dimensional dipole strength, which depends on the geometry of the bacterium, 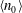$\langle n_0\rangle $ is the bacterial concentration averaged across the channel of dept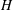h $H$, 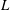$L$ is the total length of the bacterium, $\kappa $ is the bacterial diffusivity, and 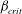$\beta _{\mathit{crit}}$ is a monotonically decreasing function of 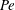${\mathit{Pe}}$, with 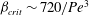$\beta _{\mathit{crit}} \sim 720/{\mathit{Pe}}^3$ for 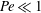${\mathit{Pe}} \ll 1$ and 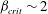$\beta _{\mathit{crit}} \sim 2$ for 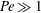${\mathit{Pe}} \gg 1$. The instability is the result of the coupling between the active stress-driven fluid flow and the bacterial concentration, and manifests as rectangular convection patterns. When 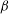$\beta $ first exceeds 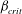$\beta _{\mathit{crit}}$, the unstable wavelengths are large with 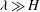$\lambda \gg H$ and the mode of instability is stationary. Although oscillatory modes appear when 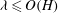$\lambda \leq O(H)$ and 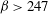$\beta > 247$, the most dangerous mode of instability is found to be always stationary with a wavelength 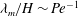$\lambda _m/H \sim {\mathit{Pe}}^{-1}$. To study the coupling between the previously analysed orientation shear instability mechanism of bacterial suspensions and the new chemotaxis-driven instability, a new set of continuum equations that consistently account for weak chemotaxis, rotation of bacteria by weak fluid shear and weak non-continuum effects along with their coupled effects has been derived. The stability analysis of those equations showed that the orientation shear mechanism has only a negligible influence on the critical concentration for the present chemotaxis-induced instability when the suspension depth is large, and it is the latter that has the lowest critical concentration.

JFM classification

Instability: Instability Biological Fluid Dynamics: Micro-organism dynamics Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 741 , 25 February 2014 , pp. 619 - 657
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1972 Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. (Applied Mathematics Series), vol. vol. 55. National Bureau of Standards, (10th printing).Google Scholar
Aderogba, K. & Blake, J. R. 1978 Action of a force near the planar surface between two semi-infinite immiscible liquids at very low Reynolds numbers. Bull. Austral. Math. Soc. 18 (3), 345–356.Google Scholar
Angelini, T. E., Roper, M., Kolter, R., Weitz, D. A. & Brenner, M. P. 2009 Bacillus subtilis spreads by surfing on waves of surfactant. Proc. Natl Acad. Sci. USA 106, 18109–18113.Google Scholar
Bearon, R. N. 2003 An extension of generalized Taylor dispersion in unbounded homogeneous shear flows to run-and-tumble chemotactic bacteria. Phys. Fluids 15, 1552–1563.Google Scholar
Bearon, R. & Pedley, T. 2000 Modelling run-and-tumble chemotaxis in a shear flow. Bull. Math. Biol. 62, 775–791.CrossRefGoogle Scholar
Berg, H. C. 2003 E. coli in Motion. Springer.Google Scholar
Berke, A. P., Turner, L, Berg, H. C. & Lauga, E. 2008 Hydrodynamic attraction of swimming microorganisms by surfaces. Phys. Rev. Lett. 101, 038102.Google Scholar
Blake, J. R. 1971 A note on the image system for a stokeslet in a no-slip boundary. Math. Proc. Camb. Philos. Soc. 70 (2), 303–310.Google Scholar
Brenner, M. P., Levitov, L. S. & Budrene, E. O. 1998 Physical mechanisms for chemotactic pattern formation by bacteria. Biophys. J. 74, 1677–1693.CrossRefGoogle ScholarPubMed
Budrene, E. O. & Berg, H. C. 1991 Complex patterns formed by motile cells of Escherichia coli. Nature 349, 630–633.Google Scholar
Budrene, E. O. & Berg, H. C. 1995 Dynamics of formation of symmetrical patterns by chemotactic bacteria. Nature 376, 49–53.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Dover.Google Scholar
Chen, K. C., Ford, R. M. & Cummings, P. T. 2003 Cell balance equation for chemotactic bacteria with a biphasic tumbling frequency. J. Math. Biol. 47, 518–546.Google Scholar
Cheng, S. Y., Heilman, S., Wasserman, M., Archer, S., Shuler, M. L. & Wu, M. 2007 A hydrogel-based microfluidic device for the studies of directed cell migration. Lab on a Chip 7, 763–769.Google Scholar
Childress, S., Levandowsky, M. & Spiegel, E. A. 1975 Pattern formation in a suspension of swimming microorganisms: equations and stability theory. J. Fluid Mech. 69, 591–613.Google Scholar
Cisneros, L., Dombrowski, C., Goldstein, R. E. & Kessler, J. O. 2006 Reversal of bacterial locomotion at an obstacle. Phys. Rev. E 73, 030901.Google Scholar
DiLuzio, W. R., Turner, L., Mayer, M., Garstecki, P., Weibel, D. B., Berg, H. C. & Whitesides, G. M. 2005 Escherichia coli swim on the right-hand side. Nature 435 (7046), 1271–1274.Google Scholar
Dombrowski, C., Cisneros, L., Chatkaew, S., Goldstein, R. E. & Kessler, J. O. 2004 Self-concentration and large-scale coherence in bacterial dynamics. Phys. Rev. Lett. 93, 098103.Google Scholar
Ezhilan, B., Pahlavan, A. A. & Saintillan, D. 2012 Chaotic dynamics and oxygen transport in thin films of aerotactic bacteria. Phys. Fluids 24 (9), 091701.Google Scholar
Ferrell, R. T. & Himmelblau, D. M. 1967 Diffusion coefficients of nitrogen and oxygen in water. J. Chem. Engng Data 12 (1), 111–115.CrossRefGoogle Scholar
Hernandez-Ortiz, J. P., Stoltz, C. G. & Graham, M. D. 2005 Transport and collective dynamics in suspensions of confined swimming particles. Phys. Rev. Lett. 95, 204501.Google Scholar
Hill, N. A., Pedley, T. J. & Kessler, J. O. 1989 Growth of bioconvection patterns in a suspension of gyrotactic micro-organisms in a layer of finite depth. J. Fluid Mech. 208, 509–543.Google Scholar
Hillesdon, A. J. & Pedley, T. J. 1996 Bioconvection in suspensions of oxytactic bacteria: linear theory. J. Fluid Mech. 324, 223–259.Google Scholar
Hohenegger, C. & Shelley, M. J. 2010 Stability of active suspensions. Phys. Rev. E 81, 046311.Google ScholarPubMed
Jánosi, I. M., Kessler, J. O. & Horváth, V. K. 1998 Onset of bioconvection in suspensions of Bacillus subtilis. Phys. Rev. E 58, 4793–4800.Google Scholar
Kalinin, Y. V., Jiang, L., Tu, Y. & Wu, W. 2009 Logarithmic sensing in Escherichia coli bacterial chemotaxis. Biophys. J. 96, 2439–2448.Google Scholar
Kasyap, T. V. & Koch, D. L. 2012 Chemotaxis driven instability of a confined bacterial suspension. Phys. Rev. Lett. 108, 038101.Google Scholar
Keller, E. F. & Segel, L. A. 1971 Model for chemotaxis. J. Theor. Biol. 30, 225–234.Google Scholar
Kim, M. J. & Breuer, K. S. 2004 Enhanced diffusion due to motile bacteria. Phys. Fluids 16, L78–L81.Google Scholar
Kim, M. J. & Breuer, K. S. 2007 Controlled mixing in microfluidic systems using bacterial chemotaxis. Analyt. Chem 79, 955–959.Google Scholar
Kim, S. & Karrila, S. J. 1991 Microhydrodynamics. Butterworth-Heinemann.Google Scholar
Koch, D. L. & Subramanian, G. 2011 Collective hydrodynamics of swimming microorganisms: living fluids. Annu. Rev. Fluid Mech. 43, 637–659.Google Scholar
Lauga, E., DiLuzio, W. R., Whitesides, G. M. & Stone, H. A. 2006 Swimming in circles: motion of bacteria near solid boundaries. Biophys. J. 90 (2), 400–412.Google Scholar
Lauga, E. & Powers, T. R. 2009 The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72, 096601.Google Scholar
Li, G. & Tang, J. X. 2009 Accumulation of microswimmers near a surface mediated by collision and rotational Brownian motion. Phys. Rev. Lett. 103, 078101.Google Scholar
Lushi, E., Goldstein, R. E. & Shelley, M. J. 2012 Collective chemotactic dynamics in the presence of self-generated fluid flows. Phys. Rev. E 86, 040902.Google Scholar
Mendelson, N. H., Bourque, A., Wilkening, K., Anderson, K. R. & Watkins, J. C. 1999 Organized cell swimming motions in Bacillus subtilis colonies: patterns of short-lived whirls and jets. J. Bacteriol. 181, 600–609.Google Scholar
Mesibov, R. & Adler, J. 1972 Chemotaxis toward amino acids in Escherichia coli. J. Bacteriol. 112, 315–326.CrossRefGoogle ScholarPubMed
Pedley, T. J. & Kessler, J. O. 1992 Hydrodynamic phenomena in suspensions of swimming microorganisms. Annu. Rev. Fluid Mech. 24, 313–358.Google Scholar
Rivero, M. A., Tranquillo, R. T., Buettner, H. M. & Lauffenburger, D. A. 1989 Transport models for chemotactic cell populations based on individual cell behaviour. Chem. Engng Sci. 44, 2881–2897.Google Scholar
Saintillan, D. & Shelley, M. J. 2007 Orientational order and instabilities in suspensions of self-locomoting rods. Phys. Rev. Lett. 99, 058102.CrossRefGoogle ScholarPubMed
Saintillan, D. & Shelley, M. J. 2008a Instabilities and pattern formation in active particle suspensions: kinetic theory and continuum simulations. Phys. Rev. Lett. 100, 178103.Google Scholar
Saintillan, D. & Shelley, M. J. 2008b Instabilities, pattern formation, and mixing in active suspensions. Phys. Fluids 20, 123304.Google Scholar
Sartori, P. & Tu, Y. 2011 Noise filtering strategies in adaptive biochemical signaling networks. J. Stat. Phys. 142 (6), 1206–1217.Google Scholar
Simha, R. A. & Ramaswamy, S. 2002 Hydrodynamic fluctuations and instabilities in ordered suspensions of self-propelled particles. Phys. Rev. Lett. 89, 058101.Google Scholar
Sokolov, A., Aranson, I. S., Kessler, J. O. & Goldstein, R. E. 2007 Concentration dependence of the collective dynamics of swimming bacteria. Phys. Rev. Lett. 98, 158102.Google Scholar
Sokolov, A., Goldstein, R. E., Feldchtein, F. I. & Aranson, I. S. 2009 Enhanced mixing and spatial instability in concentrated bacterial suspensions. Phys. Rev. E 80, 031903.Google Scholar
Stocker, R. 2011 Reverse and flick: hybrid locomotion in bacteria. Proc. Natl Acad. Sci. USA 108 (7), 2635–2636.Google Scholar
Subramanian, G. & Koch, D. L. 2009 Critical bacterial concentration for the onset of collective swimming. J. Fluid Mech. 632, 359–400.Google Scholar
Subramanian, G., Koch, D. L. & Fitzgibbon, S. R. 2011 The stability of a homogeneous suspension of chemotactic bacteria. Phys. Fluids 23, 041901.Google Scholar
Underhill, P. T., Hernandez-Ortiz, J. P. & Graham, M. D. 2008 Diffusion and spatial correlations in suspensions of swimming particles. Phys. Rev. Lett. 100, 248101.Google Scholar
Vuppula, R. R., Tirumkudulu, M. S. & Venkatesh, K. V. 2010 Chemotaxis of Escherichia coli to L-serine. Phys. Biol. 7, 026007.Google Scholar
Wu, X. L. & Libchaber, A. 2000 Particle diffusion in a quasi-two-dimensional bacterial bath. Phys. Rev. Lett. 84, 3017–3020.Google Scholar