Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
TAMMISOLA, OUTI
LUNDELL, FREDRIK
SCHLATTER, PHILIPP
WEHRFRITZ, ARMIN
and
SÖDERBERG, L. DANIEL
2011.
Global linear and nonlinear stability of viscous confined plane wakes with co-flow.
Journal of Fluid Mechanics,
Vol. 675,
Issue. ,
p.
397.
Juniper, M. P.
Tammisola, O.
and
Lundell, F.
2011.
The local and global stability of confined planar wakes at intermediate Reynolds number.
Journal of Fluid Mechanics,
Vol. 686,
Issue. ,
p.
218.
Biancofiore, Luca
Gallaire, François
and
Pasquetti, Richard
2012.
Influence of confinement on obstacle-free turbulent wakes.
Computers & Fluids,
Vol. 58,
Issue. ,
p.
27.
Biancofiore, Luca
Gallaire, François
Laure, Patrice
and
Hachem, Elie
2014.
Direct numerical simulations of two-phase immiscible wakes.
Fluid Dynamics Research,
Vol. 46,
Issue. 4,
p.
041409.
Biancofiore, Luca
2014.
Crossover between two- and three-dimensional turbulence in spatial mixing layers.
Journal of Fluid Mechanics,
Vol. 745,
Issue. ,
p.
164.
Sherratt, Jonathan A.
Dagbovie, Ayawoa S.
and
Hilker, Frank M.
2014.
A Mathematical Biologist’s Guide to Absolute and Convective Instability.
Bulletin of Mathematical Biology,
Vol. 76,
Issue. 1,
p.
1.
Balestra, Gioele
Gloor, Michael
and
Kleiser, Leonhard
2015.
Absolute and convective instabilities of heated coaxial jet flow.
Physics of Fluids,
Vol. 27,
Issue. 5,
Horvath, Camila
Arratia, Cristóbal
and
Cordero, María Luisa
2015.
Measurement of the dispersion relation of a convectively unstable capillary jet under confinement.
Physics of Fluids,
Vol. 27,
Issue. 11,
Fani, Andrea
and
Gallaire, François
2015.
The motion of a 2D pendulum in a channel subjected to an incoming flow.
Journal of Fluid Mechanics,
Vol. 764,
Issue. ,
p.
5.
Yuan, Lei
and
Shen, Chibing
2016.
Computational investigation on combustion instabilities in a rocket combustor.
Acta Astronautica,
Vol. 127,
Issue. ,
p.
634.
Jiang, Hongyi
Cheng, Liang
Draper, Scott
and
An, Hongwei
2017.
Two- and three-dimensional instabilities in the wake of a circular cylinder near a moving wall.
Journal of Fluid Mechanics,
Vol. 812,
Issue. ,
p.
435.
Han, Lei
Mignot, Emmanuel
and
Riviere, Nicolas
2017.
Shallow Mixing Layer Downstream from a Sudden Expansion.
Journal of Hydraulic Engineering,
Vol. 143,
Issue. 5,
Tammisola, Outi
Loiseau, Jean-Christophe
and
Brandt, Luca
2017.
Effect of viscosity ratio on the self-sustained instabilities in planar immiscible jets.
Physical Review Fluids,
Vol. 2,
Issue. 3,
Arratia, Cristóbal
Mowlavi, Saviz
and
Gallaire, François
2018.
Absolute/convective secondary instabilities and the role of confinement in free shear layers.
Physical Review Fluids,
Vol. 3,
Issue. 5,
MUTO, Daiki
TERASHIMA, Hiroshi
and
TSUBOI, Nobuyuki
2019.
Effects of a Recess on Supercritical Co-Flowing Planar Jets.
TRANSACTIONS OF THE JAPAN SOCIETY FOR AERONAUTICAL AND SPACE SCIENCES,
Vol. 62,
Issue. 4,
p.
203.
Martins Afonso, Marco
Meliga, Philippe
and
Serre, Eric
2019.
Optimal Transient Growth in an Incompressible Flow past a Backward-Slanted Step.
Fluids,
Vol. 4,
Issue. 1,
p.
33.
Bozonnet, Cyril
Matas, Jean-Philippe
Balarac, Guillaume
and
Desjardins, Olivier
2022.
Stability of an air–water mixing layer: focus on the confinement effect.
Journal of Fluid Mechanics,
Vol. 933,
Issue. ,
Muto, Daiki
Terashima, Hiroshi
Araki, Takahide
and
Tsuboi, Nobuyuki
2022.
Effects of a Recess on Coaxial Cryogenic Injections at Supercritical Pressure.
Journal of Propulsion and Power,
Vol. 38,
Issue. 4,
p.
581.
Vedeneev, Vasily
and
Nikitin, Nikolay
2023.
Absolute instability of plane incompressible jets.
Journal of Fluid Mechanics,
Vol. 962,
Issue. ,
Liu, Jinyuan
Puthan, Pranav
and
Sarkar, Sutanu
2024.
Effect of rotation on wake vortices in stratified flow.
Journal of Fluid Mechanics,
Vol. 999,
Issue. ,
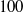 and
and 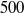 . The comparison of such limit curves with theoretical results obtained by Juniper (J. Fluid Mech., vol. 565, 2006, pp. 171–195) confirms the existence of a region at moderate confinement where the instability is maximal. Moreover, instabilities are also observed under sustained co-flow, in the form of a vacillating front. Using a direct computation of the two-dimensional base flow, we perform a local linear stability analysis for several velocity profiles prevailing at different spatial locations, so as to determine the local spatio-temporal nature of the flow: convectively unstable or absolutely unstable. Comparisons of the DNS and local stability analysis results are provided and discussed.
. The comparison of such limit curves with theoretical results obtained by Juniper (J. Fluid Mech., vol. 565, 2006, pp. 171–195) confirms the existence of a region at moderate confinement where the instability is maximal. Moreover, instabilities are also observed under sustained co-flow, in the form of a vacillating front. Using a direct computation of the two-dimensional base flow, we perform a local linear stability analysis for several velocity profiles prevailing at different spatial locations, so as to determine the local spatio-temporal nature of the flow: convectively unstable or absolutely unstable. Comparisons of the DNS and local stability analysis results are provided and discussed.