Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T07:28:02.644Z Has data issue: false hasContentIssue false
  • English
  • Français

Horizontal diffusive motion of columnar vortices in rotating Rayleigh–Bénard convection

Published online by Cambridge University Press:  21 May 2019

D. Noto Open the ORCID record for D. Noto [Opens in a new window] ,
Y. Tasaka Open the ORCID record for Y. Tasaka [Opens in a new window] ,
T. Yanagisawa  and
Y. Murai
D. Noto
Affiliation:
Laboratory for Flow Control, Faculty of Engineering, Hokkaido University, Sapporo, Japan
Y. Tasaka*
Affiliation:
Laboratory for Flow Control, Faculty of Engineering, Hokkaido University, Sapporo, Japan
T. Yanagisawa
Affiliation:
Laboratory for Flow Control, Faculty of Engineering, Hokkaido University, Sapporo, Japan Japan Agency for Marine-Earth Science and Technology (JAMSTEC), Yokosuka, Japan
Y. Murai
Affiliation:
Laboratory for Flow Control, Faculty of Engineering, Hokkaido University, Sapporo, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In laboratory experiments, horizontal translational motion of columnar vortices formed in rotating Rayleigh–Bénard convection was investigated. Two types of measurements, vertical velocity fields and horizontal temperature fields, were conducted with water as the test fluid. Using particle image velocimetry, the vertical velocity fields determined the parameter range at which the quasi-two-dimensional columnar vortices emerged. Locally, the duration characteristics of the columns, evaluated with their vertical coherence, indicate the minimum time scale of translational motion of the vortices in the horizontal plane. Vortex tracking of the horizontal temperature fields over long observation periods (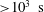${>}10^{3}~\text{s}$) was conducted using encapsulated thermochromic liquid crystal visualization. Two cylindrical vessels with different radii showed the emergence of the centrifugal effect in 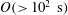$O({>}10^{2}~\text{s})$ despite the small Froude number (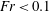$Fr<0.1$). Further, in the horizontal plane the columnar vortices behaved in a random-walk-like diffusive motion. The statistically calculated mean-squared displacements indicated anomalous diffusive motion of the columns; displacement increasing with time as 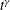$t^{\unicode[STIX]{x1D6FE}}$ with 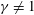$\unicode[STIX]{x1D6FE}\neq 1$. We discuss the causes of this anomaly in both the instantaneous and long-term statistical data gathered from experimental observations over different time scales. The enclosure effect from the repulsion of up-welling and down-welling vortices ensures that vortices diffuse only little, resulting in a sub-diffusive (decelerated) motion 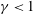$\unicode[STIX]{x1D6FE}<1$ in 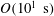$O(10^{1}~\text{s})$. With this weak centrifugal contribution, the translational motion of the columns slowly accelerates in the radial direction and thereby yields a super-diffusive (accelerated) motion 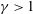$\unicode[STIX]{x1D6FE}>1$ in 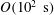$O(10^{2}~\text{s})$.

JFM classification

Geophysical and Geological Flows: Rotating flows Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 871 , 25 July 2019 , pp. 401 - 426
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdullah, N., Talib, A. R. A., Jaafar, A. A., Salleh, M. A. M. & Chonga, W. T. 2010 The basics and issues of thermochromic liquid crystal calibrations. Exp. Therm. Fluid Sci. 34, 1089–1121.Google Scholar
Aurnou, J. M., Calkins, M. A., Cheng, J. S., Julien, K., King, E. M., Nieves, D., Soderlund, K. M. & Stellmach, S. 2015 Rotating convective turbulence in earth and planetary cores. Phys. Earth Planet. Inter. 246, 52–71.Google Scholar
Boubnov, B. M. & Golitsyn, G. S. 1986 Experimental study of convective structures in rotating fluids. J. Fluid Mech. 167, 503–531.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Oxford University Press.Google Scholar
Cheng, J. S., Aurnou, J. M., Julien, K. & Kunnen, R. P. J. 2018 A heuristic framework for next-generation models of geostrophic convective turbulence. Geophys. Astrophys. Fluid Dyn. 112 (4), 277–300.Google Scholar
Cheng, J. S., Stellmach, S., Ribeiro, A., Grannan, A., King, E. M. & Aurnou, J. M. 2015 Laboratory-numerical models of rapidly rotating convection in planetary cores. Geophys. J. Intl 201, 1–17.Google Scholar
Grannan, A. M., Favier, B., Le Bars, M. & Aurnou, J. M. 2016 Tidally forced turbulence in planetary interiors. Geophys. J. Intl 208 (3), 1690–1703.Google Scholar
Grooms, I., Julien, K., Weiss, J. B. & Knobloch, E. 2010 Model of convective Taylor column in rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 104, 224501.Google Scholar
Horn, S. & Aurnou, J. M. 2018 Regimes of Coriolis–centrifugal convection. Phys. Rev. Lett. 120 (20), 204502.Google Scholar
Jones, C. A. 2011 Planetary magnetic fields and fluid dynamos. Annu. Rev. Fluid Mech. 43, 583–614.Google Scholar
Julien, K., Aurnou, J. M., Calkins, M. A., Knobloch, E., Marti, P., Stellmach, S. & Vasil, G. M. 2016 A nonlinear model for rotationally constrained convection with Ekman pumping. J. Fluid Mech. 798, 50–87.Google Scholar
Julien, K., Legg, S., McWilliams, J. & Werne, J. 1996 Rapidly rotating turbulent Rayleigh–Bénard convection. J. Fluid Mech. 322, 243–273.Google Scholar
Julien, K., Rubio, A. M., Grooms, I. & Knobloch, E. 2012 Statistical and physical balances in low Rossby number Rayleigh–Bénard convection. Geophys. Astrophys. Fluid Dyn. 106, 392–428.Google Scholar
Kunnen, R. P. J., Clercx, H. J. H. & Geurts, B. J. 2010 Vortex statics in turbulent rotating convection. Phys. Rev. E 82 (3), 036306.Google Scholar
Kunnen, R. P. J., Corre, Y. & Clercx, H. J. H. 2014 Vortex plume distribution in confined turbulent rotating convection. Eur. Phys. Lett. 104 (5), 54002.Google Scholar
Liu, Y. & Ecke, R. E. 2009 Heat transport measurements in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. E 80, 036314.Google Scholar
Meuel, T., Prado, G., Seychelles, F., Bessafi, M. & Kellay, H. 2012 Hurricane track forecast cones from fluctuations. Sci. Rep. 2, 446.Google Scholar
Noto, D., Tasaka, Y., Yanagisawa, T., Park, H. J. & Murai, Y. 2018 Vortex tracking on visualized temperature fields in a rotating Rayleigh–Bénard convection. J. Vis. 21, 987–998.Google Scholar
Pieri, A. B., Falasca, F., Hardenberg, J. V. & Provenzale, A. 2016 Plume dynamics in rotating Rayleigh–Bénard convection. Phys. Lett. A 380, 1363–1367.Google Scholar
Rajaei, H., Kunnen, R. P. J. & Clercx, H. J. H. 2017 Exploring the geostrophic regime of rapidly rotating convection with experiments. Phys. Fluids 29 (4), 045105.Google Scholar
Rao, Y. & Zang, S. 2010 Calibrations and the measurement uncertainty of wide-band liquid crystal thermography. Meas. Sci. Technol. 21, 015105.Google Scholar
Sakai, S. 1997 The horizontal scale of rotating convection in the geostrophic regime. J. Fluid Mech. 333, 85–95.Google Scholar
Shlesinger, M. F., Zaslavsky, G. M. & Klafter, J. 1993 Strange kinetics. Nature 363 (6424), 31–37.Google Scholar
Solomon, T. H., Weeks, E. R. & Swinney, H. L. 1993 Observation of anomalous diffusion and Lévy flights in a two-dimensional rotating flow. Phys. Rev. Lett. 71 (24), 3975–3978.Google Scholar
Sprague, M., Julien, K., Knobloch, E. & Werne, J. 2006 Numerical simulation of an asymptotically reduced system for rotationally constrained convection. J. Fluid Mech. 551, 141–174.Google Scholar
Stellmach, S., Lischper, M., Julien, K., Vasil, G., Cheng, J. S., Ribeiro, A., King, E. M. & Aurnou, J. M. 2014 Approaching the asymptotic regime of rapidly rotating convection: boundary layers versus interior dynamics. Phys. Rev. Lett. 113, 254501.Google Scholar
Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2012 Breakdown of the large-scale wind in 𝛾 = 1/2 rotating Rayleigh–Bénard flow. Phys. Rev. E 86, 056311.Google Scholar
Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2013 Heat transport and flow structure in rotating Rayleigh–Bénard convection. Eur. J. Mech. (B/Fluids) 40, 41–49.Google Scholar
Vorobieff, P. & Ecke, R. E. 1998 Vortex structure in rotating Rayleigh–Bénard convection. Physica D 123, 153–160.Google Scholar
Vorobieff, P. & Ecke, R. E. 2002 Turbulent rotating convection: an experimental study. J. Fluid Mech. 458, 191–218.Google Scholar
Weiss, S. & Ahlers, G. 2011 Heat transport by turbulent rotating Rayleigh–Bénard convection and its dependence on the aspect ratio. J. Fluid Mech. 309, 1–20.Google Scholar
Wiberg, R. & Lior, N. 2004 Errors in thermochromic liquid crystal thermometry. Rev. Sci. Instrum. 75, 2985–2994.Google Scholar
Zhong, F., Ecke, R. E. & Steinberg, V. 1993 Rotating Rayleigh–Bénard convection: asymmetric modes and vortex states. J. Fluid Mech. 249, 135–159.Google Scholar