Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-01T01:59:01.854Z Has data issue: false hasContentIssue false
  • English
  • Français

Heat transfer and shear-induced migration in dense non-Brownian suspension flows: modelling and simulation

Published online by Cambridge University Press:  13 February 2018

T. Dbouk Open the ORCID record for T. Dbouk [Opens in a new window]
T. Dbouk*
Affiliation:
IMT Lille Douai, Energy Engineering Department, 59500 Douai, France University of Lille, 59000 Lille, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Modelling and simulation are developed, generalized and validated for both heat transfer and shear-induced particle migration in dense non-colloidal laminar suspension flows. Past theory and measurements for the effective thermal conductivity in porous materials at zero shear rate are coupled to more recent effective thermal diffusivity measurements of sheared suspensions. The suspension effective heat transfer affected by the local shear rate ($\dot{\unicode[STIX]{x1D6FE}}$), the phenomenon of shear-induced particle migration (SIM), the buoyancy effects ($\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$) and the thermal Péclet number (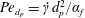$Pe_{d_{p}}=\dot{\unicode[STIX]{x1D6FE}}d_{p}^{2}/\unicode[STIX]{x1D6FC}_{f}$, where 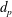$d_{p}$ is the diameter of rigid particles and 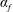$\unicode[STIX]{x1D6FC}_{f}$ is the fluid phase thermal diffusivity) at the particle scale are all considered in the present constitutive three-dimensional modelling. Moreover, the influence of the temperature, the shear rate and the particle volume fraction ($\unicode[STIX]{x1D719}$) on the suspension effective viscosity ($\unicode[STIX]{x1D702}_{S}$), the suspension effective thermal properties and the fluid density (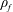$\unicode[STIX]{x1D70C}_{f}$) are taken also into account. The present contribution represents an emerging field of heat transfer applications of complex fluid flows and is very beneficial for many future applications where concentrated suspension laminar flows with conjugate heat transfer may be present (e.g. for designing more innovative and compact heat exchangers).

JFM classification

Mathematical Foundations: Computational methods Multiphase and Particle-laden Flows: Multiphase flow Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 840 , 10 April 2018 , pp. 432 - 454
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahuja, A. S. 1975a Augmentation of heat transport in laminar flow of polystyrene suspensions. I. Experiments and results. J. Appl. Phys. 48, 3408–3416.CrossRefGoogle Scholar
Ahuja, A. S. 1975b Augmentation of heat transport in laminar flow of polystyrene suspensions. II. Analysis of the data. J. Appl. Phys. 48, 3417–3425.Google Scholar
Andreotti, B., Forterre, Y. & Pouliquen, O. 2013 Granular Media: Between Fluid and Solid. Cambridge University Press.Google Scholar
Boyer, F., Guazzelli, É. & Pouliquen, O. 2011a Unifying suspension and granular rheology. Phys. Rev. Lett. 107, 188301.Google Scholar
Boyer, F., Pouliquen, O. & Guazzelli, É. 2011b Dense suspensions in rotating-rod flows: normal stresses and particle migration. J. Fluid Mech. 686, 5–25.Google Scholar
Bricker, J. M. & Butler, J. E. 2006 Oscillatory shear of suspensions of noncolloidal particles. J. Rheol. 50 (5), 711–728.CrossRefGoogle Scholar
Chapman, B.1990 Shear-induced migration phenomena in concentrated suspensions. PhD thesis, University of Notre Dame, Indiana, USA.Google Scholar
Chow, A. W., Sinton, S. W., Iwamiya, J. H. & Stephens, T. S. 1994 Shear-induced migration in Couette and parallel-plate viscometers: Nmr imaging and stress measurements. Phys. Fluids 6, 2561.Google Scholar
Coble, R. L. & Kingery, W. D. 1956 Effect of porosity on physical properties of sintered alumina. J. Am. Ceram. Soc. 39, 377–385.CrossRefGoogle Scholar
Davis, R. H. & Acrivos, A. 1985 Sedimentation of non-colloidal particles at low Reynolds numbers. Annu. Rev. Fluid Mech. 17, 91–118.CrossRefGoogle Scholar
Dbouk, T.2011 Rheology of concentrated suspensions and shear-induced migration. PhD thesis, University of Nice-Sophia Antipolis, Nice, France.Google Scholar
Dbouk, T. 2016 A suspension balance direct-forcing immersed boundary model for wet granular flows over obstacles. J. Non-Newtonian Fluid Mech. 230, 68–79.Google Scholar
Dbouk, T., Lobry, L. & Lemaire, E. 2013a Normal stresses in concentrated non-Brownian suspensions. J. Fluid Mech. 715, 239–272.Google Scholar
Dbouk, T., Lobry, L., Lemaire, E. & Moukalled, F. 2013b Shear-induced particles migration; predictions from experimental determination of the particle stress tensor. J. Non-Newtonian Fluid Mech. 198, 78–95.Google Scholar
Eucken, A. 1932 Thermal conductivity of ceramic refractory materials, calculation from thermal conductivity of constituents. VDI Forsch. 353, 16.Google Scholar
Ferziger, J. H. & Peric, M. 2002 Computational Methods for Fluid Dynamics. Springer.Google Scholar
Gadala-Maria, F. & Acrivos, A. 1980 Shear-induced structure in a concentrated suspension of solid spheres. J. Rheol. 24, 799.Google Scholar
Gallier, S., Lemaire, E., Lobry, L. & Peters, F. 2016 Effect of confinement in wall-bounded non-colloidal suspensions. J. Fluid Mech. 799, 100–127.Google Scholar
Guazzelli, É. 2017 Rheology of dense suspensions of non colloidal particles. Powders and Grains EPJ Web of Conferences 140, 01001.Google Scholar
Guazzelli, É. & Morris, J. 2011 A Physical Introduction to Suspension Dynamics, Cambridge Texts in Applied Mathematics. Cambridge University Press.CrossRefGoogle Scholar
Kim, J. M., Lee, S. G. & Kim, D. C. 2008 Numerical simulations of particle migration in suspension flows: frame-invariant formulation of curvature-induced migration. J. Non-Newtonian Fluid Mech. 150, 162.CrossRefGoogle Scholar
Krieger, I. M. & Dougherty, T. 1959 A mechanism for non-Newtonian flow in suspensions of rigid spheres. Soc. Rheol. 3, 137.Google Scholar
Leighton, D. & Acrivos, A. 1987a Measurement of self-diffusion in concentrated suspensions of spheres. J. Fluid Mech. 177, 109–131.Google Scholar
Leighton, D. & Acrivos, A. 1987b The shear-induced migration of particles in concentrated suspensions. J. Fluid Mech. 181, 415–439.Google Scholar
Lhuillier, D. 2009 Migration of rigid particles in non-Brownian viscous suspensions. Phys. Fluids 21, 023302.CrossRefGoogle Scholar
Lyczkowski, R. W., Solbirg, C. W. & Gidaspow, D.1969 Forced convective heat transfer in rectangular ducts – general case of wall resistances and peripheral conduction. Institute of Gas Technology, Tech. Info. Center III. 60616, 3229–3424 S. State Street, Chicago.Google Scholar
Lyon, M. K. & Leal, L. G. 1998 An experimental study of the motion of concentrated suspensions in two-dimensional channel flow. Part 1. Monodisperse systems. J. Fluid Mech. 363, 25–56.Google Scholar
Maxwell, J. C. 1873 A Treatise on Electricity and Magnetism. Clarendon.Google Scholar
Merhi, D., Lemaire, E., Bossis, G. & Moukalled, F. 2005 Particle migration in a concentrated suspension flowing between rotating parallel plates: investigation of diffusion flux coefficients. J. Rheol. 49, 1429.CrossRefGoogle Scholar
Metzger, B., Rahli, O. & Yin, X. 2013 Heat transfer across sheared suspensions: role of the shear-induced diffusion. J. Fluid Mech. 724, 527–552.Google Scholar
Miller, R. M. & Morris, J. F. 2006 Normal stress-driven migration and axial development in pressure-driven flow of concentrated suspensions. J. Non-Newtonian Fluid Mech. 135, 149–165.CrossRefGoogle Scholar
Morris, J. F. & Boulay, F. 1999 Curvilinear flows of non-colloidal suspensions: the role of normal stresses. J. Rheol. 43, 1213–1237.Google Scholar
Morris, J. F. & Brady, J. F. 1998 Pressure-driven flow of a suspension: buoyancy effects. Intl J. Multiphase Flow 24, 105–130.CrossRefGoogle Scholar
Moukalled, F., Mangani, L. & Darwish, M. 2015 The Finite Volume Method in Computational Fluid Dynamics. An Advanced Introduction with OpenFOAM® and Matlab® . Springer.Google Scholar
Nott, P. R. & Brady, J. F. 1994 Pressure-driven flow of suspensions: simulation and theory. J. Fluid Mech. 275, 157.Google Scholar
OpenFOAM2017 Openfoam (open field operation and manipulation) open source cfd toolbox.Google Scholar
Pabst, W. 2004 Simple second-order expression: for the porosity dependence of thermal conductivity. J. Mater. Sci. 40, 2667–2669.Google Scholar
Peters, F., Ghigliotti, G., Gallier, S., Blanc, F., Lemaire, E. & Lobry, L. 2016 Rheology of non-Brownian suspensions of rough frictional particles under shear reversal: a numerical study. J. Rheol. 60, 715.Google Scholar
Phillips, R. J., Armstrong, R. C., Brown, R. A., Graham, A. & Abbott, J. R. 1992 A constitutive model for concentrated suspensions that accounts for shear-induced particle migration. Phys. Fluids A 4, 30–40.Google Scholar
Rebouas, R. B., Siqueira, I. R., de Souza Mendes, P. R. & Carvalho, M. S. 2016 On the pressure-driven flow of suspensions: particle migration in shear sensitive liquids. J. Non-Newtonian Fluid Mech. 234, 178–187.CrossRefGoogle Scholar
Ribaud, M. 1937 Theoretical study of the thermal conductivity of porous and pulverulent materials. Chaleur et ind. 118, 36.Google Scholar
Richardson, J. F. & Zaki, W. N. 1954 Sedimentation and fluidization: part I. Trans. Inst. Chem. Engrs 32, 35–47.Google Scholar
Russell, H. W. 1935 Principles of heat flow in porous insulators. J. Am. Ceram. Soc. 18, 1–12.Google Scholar
Semwogerere, D., Morris, J. F. & Weeks, E. R. 2007 Development of particle migration in pressure-driven flow of a Brownian suspension. J. Fluid Mech. 581, 437–451.Google Scholar
Shah, R. K. & London, A. L. 1974 Thermal boundary conditions and some solutions for laminar duct flow forced convection. Trans. ASME J. Heat Transfer 96 (2), 159–165.CrossRefGoogle Scholar
Shah, R. K. & London, A. L. 1978 Laminar Flow Forced Convection in Ducts. Academic Press.Google Scholar
Shin, S. & Lee, S. 2000 Thermal conductivity of suspensions in shear flow fields. Intl J. Heat Mass Transfer 43, 4275–4284.Google Scholar
Sohn, C. W. & Chen, M. M. 1981 Microconvective thermal conductivity in disperse two-phase mixtures as observed in a low velocity Couette flow experiment. Trans. ASME J. Heat Transfer 103, 47–51.CrossRefGoogle Scholar
Sugawara, A. & Yoshizawa, Y. 1961 An investigation of the thermal conductivity of porous materials and its application to porous rock. Austral. J. Phys. 14, 169–480.Google Scholar
Sugawara, A. & Yoshizawa, Y. 1962 An experimental investigation on the thermal conductivity of consolidated porous materials. J. Appl. Phys. 33, 3135.Google Scholar
Wibulswas, P.1966 Laminar-flow heat transfer in non-circular ducts. PhD thesis, London University, London, UK.Google Scholar
Wu, W. T., Zhou, Z. F., Aubry, N., Antaki, J. F. & Massoudi, M. 2017 Heat transfer and flow of a dense suspension between two cylinders. Intl J. Heat Mass Transfer 112, 597–606.Google Scholar