Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-01-08T21:51:38.079Z Has data issue: false hasContentIssue false
  • English
  • Français

Haemorheology in dilute, semi-dilute and dense suspensions of red blood cells

Published online by Cambridge University Press:  14 June 2019

Naoki Takeishi Open the ORCID record for Naoki Takeishi [Opens in a new window] ,
Marco E. Rosti Open the ORCID record for Marco E. Rosti [Opens in a new window] ,
Yohsuke Imai Open the ORCID record for Yohsuke Imai [Opens in a new window] ,
Shigeo Wada  and
Luca Brandt Open the ORCID record for Luca Brandt [Opens in a new window]
Naoki Takeishi*
Affiliation:
Graduate School of Engineering Science, Osaka University, 1-3 Machikaneyama, Toyonaka, Osaka 560-8531, Japan
Marco E. Rosti
Affiliation:
Linné Flow Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE 100 44 Stockholm, Sweden
Yohsuke Imai
Affiliation:
Graduate School of Engineering, Kobe University, 1-1 Rokkodai, Nada, Kobe 657-8501, Japan
Shigeo Wada
Affiliation:
Graduate School of Engineering Science, Osaka University, 1-3 Machikaneyama, Toyonaka, Osaka 560-8531, Japan
Luca Brandt
Affiliation:
Linné Flow Centre and SeRC (Swedish e-Science Research Centre), KTH Mechanics, SE 100 44 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a numerical analysis of the rheology of a suspension of red blood cells (RBCs) in a wall-bounded shear flow. The flow is assumed as almost inertialess. The suspension of RBCs, modelled as biconcave capsules whose membrane follows the Skalak constitutive law, is simulated for a wide range of viscosity ratios between the cytoplasm and plasma, 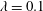$\unicode[STIX]{x1D706}=0.1$–10, for volume fractions up to 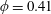$\unicode[STIX]{x1D719}=0.41$ and for different capillary numbers (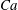$Ca$). Our numerical results show that an RBC at low 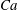$Ca$ tends to orient to the shear plane and exhibits so-called rolling motion, a stable mode with higher intrinsic viscosity than the so-called tumbling motion. As 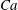$Ca$ increases, the mode shifts from the rolling to the swinging motion. Hydrodynamic interactions (higher volume fraction) also allow RBCs to exhibit tumbling or swinging motions resulting in a drop of the intrinsic viscosity for dilute and semi-dilute suspensions. Because of this mode change, conventional ways of modelling the relative viscosity as a polynomial function of 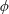$\unicode[STIX]{x1D719}$ cannot be simply applied in suspensions of RBCs at low volume fractions. The relative viscosity for high volume fractions, however, can be well described as a function of an effective volume fraction, defined by the volume of spheres of radius equal to the semi-middle axis of a deformed RBC. We find that the relative viscosity successfully collapses on a single nonlinear curve independently of 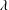$\unicode[STIX]{x1D706}$ except for the case with 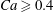$Ca\geqslant 0.4$, where the fit works only in the case of low/moderate volume fraction, and fails in the case of a fully dense suspension.

JFM classification

Biological Fluid Dynamics: Blood flow Biological Fluid Dynamics: Capsule/cell dynamics Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 872 , 10 August 2019 , pp. 818 - 848
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abkarian, M., Faivre, M. & Viallat, A. 2007 Swinging of red blood cells under shear flow. Phys. Rev. Lett. 98, 188302.Google Scholar
Barthés-Biesel, D. 1980 Motion of a spherical microcapsule freely suspended in a linear shear flow. J. Fluid. Mech. 100, 831–853.Google Scholar
Barthés-Biesel, D. & Sgaier, H. 1985 Role of membrane viscosity in the orientation and deformation of a spherical capsule suspended in shear flow. J. Fluid. Mech. 160, 119–135.Google Scholar
Batchelor, G. K. 1970 The stress system in a suspension of force-free particles. J. Fluid Mech. 41, 545–570.Google Scholar
Bhatnagar, P. L., Gross, E. P. & Krook, M. 1954 A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94, 511–525.Google Scholar
Brooks, D. E., Goodwin, J. W. & Seaman, G. V. 1970 Interactions among erythrocytes under shear. J. Appl. Physiol. 28, 172–177.Google Scholar
Chen, S. & Doolen, G. D. 1998 Lattice Boltzmann method for fluid flow. Annu. Rev. Fluid Mech. 30, 329–364.Google Scholar
Chien, S. 1970 Shear dependence of effective cell volume as a determinant of blood viscosity. Science 168, 977–979.Google Scholar
Chien, S., Usami, S. & Bertles, J. F. 1970 Abnormal rheology of oxygenated blood in sickle cell anemia. J. Clin. Invest. 49, 623–634.Google Scholar
Clausen, J. R., Reasor, D. A. Jr & Aidun, C. K. 2011 The rheology and microstructure of concentrated non-colloidal suspensions of deformable capsules. J. Fluid Mech. 685, 202–234.Google Scholar
Cokelet, G. R. & Meiselman, H. J. 1968 Rheological comparison of hemoglobin solutions and erythrocyte suspensions. Science 162, 275–277.Google Scholar
Cokelet, G. R. & Meiselman, H. J. 2007 Macro and micro rheological properties of blood. In Handbook of Hemorheology and Hemodynamics, pp. 45–71. IOS Press.Google Scholar
Cordasco, D. & Bagchi, P. 2014 Orbital drift of capsules and red blood cells in shear flow. Phys. Fluids 25, 091902.Google Scholar
Cordasco, D., Yazdani, A. & Bagchi, P. 2014 Comparison of erythrocyte dynamics in shear flow under different stress-free configurations. Phys. Fluids 26, 041902.Google Scholar
Dintenfass, L. & Somer, T. 1975 On the aggregation of red cells in Waldenström’s macroglobulinaemia and multiple myeloma. Microvasc. Res. 9, 279–286.Google Scholar
Dupin, M. M., Halliday, I., Care, C. M., Alboul, L. & Munn, L. L. 2007 Modeling the flow of dense suspensions of deformable particles in three dimensions. Phys. Rev. E 75, 066707.Google Scholar
Dupire, J., Abkarian, M. & Viallat, A. 2010 Chaotic dynamics of red blood cells in a sinusoidal flow. Phys. Rev. Lett. 104, 168101.Google Scholar
Dupire, J., Socol, M. & Viallat, A. 2012 Full dynamics of a red blood cell in shear flow. Proc. Natl Acad. Sci. USA 109, 20808–20813.Google Scholar
Einstein, A. 1911 Berichtigung zu meiner Arbeit:Eine neue Bestimmung der Moleküldimensionen. Ann. Phys. 34, 591–592.Google Scholar
Embury, S. H., Clark, M. R., Monroy, G. & Mohandas, N. 1984 Concurrent sickle cell anemia and alpha-thalassemia. Effect on pathological properties of sickle erythrocytes. J. Clin. Invest. 73, 116–123.Google Scholar
Evans, E., Mohandas, N. & Leung, A. 1984 Static and dynamic rigidities of normal and sickle erythrocytes. Major influence of cell hemoglobin concentration. J. Clin. Invest. 73, 477–488.Google Scholar
Fedosov, D. A., Panb, W., Caswell, B., Gomppera, G. & Karniadakis, G. E. 2011 Predicting human blood viscosity in silico. Proc. Natl Acad. Sci. USA 108, 11772–11777.Google Scholar
Fischer, T. M. 2004 Shape memory of human red blood cells. Biophys. J. 86, 3304–3313.Google Scholar
Fischer, T. M., Stöhr-Liesen, M. & Schmid-Schönbein, H. 1978 The red cell as a fluid droplet: tank tread-like motion of the human erythrocyte membrane in shear flow. Science 202, 894–896.Google Scholar
Foessel, É., Walter, J., Salsac, A.-V. & Barthés-Biesel, D. 2011 Influence of internal viscosity on the large deformation and buckling of a spherical capsule in a simple shear flow. J. Fluid Mech. 672, 477–486.Google Scholar
Freund, J. B. 2007 Leukocyte margination in a model microvessel. Phys. Fluids 19, 023301.Google Scholar
Goldsmith, H. L. 1972 The microrheology of human erythrocyte suspensions. In Proc. 13th IUTAM Congress on Theoretical and Applied Mechanics (ed. Becker, E. & Mikhailov, G. K.), pp. 85–103. Springer.Google Scholar
Gross, M., Krüger, T. & Varnik, F. 2014 Rheology of dense suspensions of elastic capsules: normal stresses, yield stress, jamming and confinement effects. Soft Matt. 10, 4360–4372.Google Scholar
Harkness, J. & Whittington, R. B. 1970 Blood-plasma viscosity: an approximate temperature-invariant arising from generalised concepts. Biorheology 6, 169–187.Google Scholar
Henríquez-Rivera, R. G., Sinha, K. & Graham, M. D. 2015 Margination regimes and drainage transition in confined multicomponent suspensions. Phys. Rev. Lett. 114, 188101.Google Scholar
Ishikawa, T. 2012 Vertical dispersion of model microorganisms in horizontal shear flow. J. Fluid Mech. 705, 98–119.Google Scholar
Ito, H., Murakami, R., Sakuma, S., Tsai, C.-H. D., Gutsmann, T., Brandenburg, K., Pöschl, J. M. B., Arai, F., Kaneko, M. & Tanaka, M. 2017 Mechanical diagnosis of human erythrocytes by ultra-high speed manipulation unraveled critical time window for global cytoskeletal remodeling. Sci. Rep. 7, 43134.Google Scholar
Jeffery, D. J., Morris, J. F. & Brandy, J. F. 1993 The pressure moments for two rigid spheres in low-Reynolds-number flow. Phys. Fluids A 5, 2317–2325.Google Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161–179.Google Scholar
Kaul, D. K. & Xue, H. 1991 Rate of deoxygenation and rheologic behavior of blood in sickle cell anemia. Blood 77, 1353–1361.Google Scholar
Koutsiaris, A. G., Tachmitzi, S. V. & Batis, N. 2013 Wall shear stress quantification in the human conjunctival pre-capillary arterioles in vivo . Microvasc. Res. 85, 34–39.Google Scholar
Koutsiaris, A. G., Tachmitzi, S. V., Batis, N., Kotoula, M. G., Karabatsas, C. H., Tsironi, E. & Chatzoulis, D. Z. 2007 Volume flow and wall shear stress quantification in the human conjunctival capillaries and post-capillary venules in vivo . Biorheology 44, 375–386.Google Scholar
Krieger, I. M. & Dougherty, T. J. 1959 A mechanism for non-Newtonian flow in suspensions of rigid spheres. Trans. Soc. Rheol. 3, 137–152.Google Scholar
Krüger, T., Varnik, F. & Raabe, D. 2011 Particle stress in suspensions of soft objects. Trans. R. Soc. Lond. A 369, 2414–2421.Google Scholar
Kumar, A., Henríquez-Rivera, R. G. & Graham, M. D. 2014 Flow-induced segregation in confined multicomponent suspensions: effects of particle size and rigidity. J. Fluid Mech. 738, 423–462.Google Scholar
Lanotte, L., Mauer, J., Mendez, S., Fedosov, D. A., Fromental, J.-M., Claveria, V., Nicoul, F., Gompper, G. & Abkarian, M. 2016 Red cells’ dynamic morphologies govern blood shear thinning under microcirculatory flow conditions. Proc. Natl Acad. Sci. USA 113, 13289–13294.Google Scholar
Lees, A. W. & Edwards, S. F. 1972 The computer study of transport processes under extreme conditions. J. Phys. C 1, 1921–1928.Google Scholar
Li, J., Dao, M., Lim, C. T. & Suresh, S. 2005 Spectrin-level modeling of the cytoskeleton and optical tweezers stretching of the erythrocyte. Phys. Fluids 88, 3707–6719.Google Scholar
Matsunaga, D., Imai, Y., Yamaguchi, T. & Ishikawa, T. 2016 Rheology of a dense suspension of spherical capsules under simple shear flow. J. Fluid Mech. 786, 110–127.Google Scholar
Mauer, J., Mendez, S., Lanotte, L., Nicoud, F., Abkarian, M., Gompper, G. & Fedosov, D. A. 2018 Flow-induced transitions of red blood cell shapes under shear. Phys. Rev. Lett. 121, 118103.Google Scholar
Miki, T., Wang, X., Aoki, T., Imai, Y., Ishikawa, T., Takase, K. & Yamaguchi, T. 2012 Patient-specific modeling of pulmonary air flow using GPU cluster for the application in medical particle. Comput. Meth. Biomech. Biomed. Engng 15, 771–778.Google Scholar
Mohandas, N. & Gallagher, P. G. 2008 Red cell membrane: past, present, and future. Blood 112, 3939–3948.Google Scholar
Omori, T., Imai, Y., Yamaguchi, T. & Ishikawa, T. 2012 Reorientation of a non-spherical capsule in creeping shear flow. Phys. Rev. Lett. 108, 138102.Google Scholar
Omori, T., Ishikawa, T., Imai, Y. & Yamaguchi, T. 2014 Hydrodynamic interaction between two red blood cells in simple shear flow: its impact on the rheology of a semi-dilute suspension. Comput. Mech. 54, 933–941.Google Scholar
Pedley, T. J. 1980 The Fluid Mechanics of Large Blood Vessels. Cambridge University Press.Google Scholar
Peng, Z., Mashayekh, A. & Zhu, Q. 2014 Erythrocyte responses in low-shear-rate flows: effects of non-biconcave stress-free state in the cytoskeleton. J. Fluid. Mech. 742, 96–118.Google Scholar
Peskin, C. S. 2002 The immersed boundary method. Acta Numerica 11, 479–517.Google Scholar
Picano, F., Breugem, W. P., Mitra, D. & Brandt, L. 2013 Shear thickening in non-Brownian suspensions: an excluded volume effect. Phys. Rev. Lett. 111, 098302.Google Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.Google Scholar
Puig-de-Morales-Marinkovic, M., Turner, K. T., Butler, J. P., Fredberg, J. J. & Suresh, S. 2007 Viscoelasticity of the human red blood cell. Am. J. Physiol. Cell Physiol. 293, C597–C605.Google Scholar
Ramanujan, S. & Pozrikidis, C. 1998 Deformation of liquid capsules enclosed by elastic membranes in simple shear flow: large deformations and the effect of fluid viscosities. J. Fluid Mech. 361, 117–143.Google Scholar
Reasor, D. A. Jr, Clausen, J. R. & Aidun, C. K. 2013 Rheological characterization of cellular blood in shear. J. Fluid Mech. 726, 497–516.Google Scholar
Rosti, M. E. & Brandt, L. 2018 Suspensions of deformable particles in a Couette flow. J. Non-Newtonian Fluid Mech. 262C, 3–11.Google Scholar
Rosti, M. E., Brandt, L. & Mitra, D. 2018 Rheology of suspensions of viscoelastic spheres: deformability as an effective volume fraction. Phys. Rev. Fluids 3, 012301.Google Scholar
Schmid-Schönbein, H. & Wells, R. 1969 Fluid drop-like transition of erythrocytes under shear. Science 165, 288–291.Google Scholar
Secomb, T. W. 2017 Blood flow in the microcirculation. Annu. Rev. Fluid Mech. 49, 443–461.Google Scholar
Sinha, K. & Graham, M. D. 2015 Dynamics of a single red blood cell in simple shear flow. Phys. Rev. E 92, 042710.Google Scholar
Skalak, R., Tozeren, A., Zarda, R. P. & Chien, S. 1973 Strain energy function of red blood cell membranes. Biophys. J. 13, 245–264.Google Scholar
Skovborg, F., Nielsen, A. A. V., Schlichtkrull, J. & Ditzel, J. 1966 Blood-viscosity in diabetic patients. Lancet 287, 129–131.Google Scholar
Somer, T. 1987 Rheology of paraproteinaemias and the plasma hyperviscosity syndrome. Bailliére’s Clin. Haematol. 1, 695–723.Google Scholar
Stickel, J. J. & Powell, R. L. 2005 Fluid mechanics and rheology of dense suspensions. Annu. Rev. Fluid Mech. 37, 129–149.Google Scholar
Suresh, S., Spatz, J., Mills, J. P., Micoulet, A., Dao, M., Lim, C. T., Beil, M. & Seufferlein, T. 2005 Connections between single-cell biomechanics and human diseases states: gastrointestinal cancer and malaria. Acta Biomater. 1, 15–30.Google Scholar
Takeishi, N. & Imai, Y. 2017 Capture of microparticles by bolus of red blood cells in capillaries. Sci. Rep. 7, 5381.Google Scholar
Takeishi, N., Imai, Y., Ishida, S., Omori, T., Kamm, R. D. & Ishikawa, T. 2016 Cell adhesion during bullet motion in capillaries. Am. J. Physiol. Heart Circ. Physiol. 311, H395–H403.Google Scholar
Takeishi, N., Imai, Y., Nakaaki, K., Yamaguchi, T. & Ishikawa, T. 2014 Leukocyte margination at arteriole shear rate. Physiol. Rep. 2, e12037.Google Scholar
Takeishi, N., Imai, Y. & Wada, S. 2019 Capture event of platelets by bolus flow of red blood cells in capillaries. J. Biomech. Sci. Engng (submitted), https://www.jstage.jst.go.jp/article/jbse/advpub/0/advpub_18-00535/_article.Google Scholar
Takeishi, N., Imai, Y., Yamaguchi, T. & Ishikawa, T. 2015 Flow of a circulating tumor cell and red blood cells in microvessels. Phys. Rev. E 92, 063011.Google Scholar
Tao, R. & Huang, K. 2011 Reducing blood viscosity with magnetic fields. Phys. Rev. E 84, 011905.Google Scholar
Taylor, G. T. 1923 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 58–61.Google Scholar
Taylor, G. T. 1932 The viscosity of a fluid containing small drops of another fluid. Proc. R. Soc. Lond. A 138, 41–48.Google Scholar
Tsubota, K., Wada, S. & Liu, H. 2014 Elastic behavior of a red blood cell with the membrane’s nonuniform natural state: equilibrium shape, motion transition under shear flow, and elongation during tank-treading motion. Biomech. Model. Mechanobiol. 13, 735–746.Google Scholar
Unverdi, S. O. & Tryggvason, G. 1992 A front-tracking method for viscous, incompressible, multi-fluid flows. J. Comput. Phys. 100, 25–37.Google Scholar
Usami, S., Chien, S., Scholtz, P. M. & Bertles, J. F. 1975 Effect of deoxygenation on blood rheology in sickle cell disease. Microvasc. Res. 9, 324–334.Google Scholar
Walter, J., Salsac, A. V., Barthés-Biesel, D. & Tallec, P. L. 2010 Coupling of finite element and boundary integral methods for a capsule in a stokes flow. Intl J. Numer. Meth. Engng 83, 829–850.Google Scholar
Xiao, F., Honma, Y. & kono, T. 2005 A simple algebraic interface capturing scheme using hyperbolic tangent function. Intl J. Numer. Meth. Fluids 48, 1023–1040.Google Scholar
Yokoi, K. 2007 Efficient implementation of THINC scheme: a simple and practical smoothed VOF algorithm. J. Comput. Phys. 226, 1985–2002.Google Scholar

Takeishi et al. supplementary movie 1

Tumbling RBC for Ca = 0.05 and λ = 5.0. The initial orientation angle is Ψ0 = π/2.

Download Takeishi et al. supplementary movie 1(Video)
Video 3.3 MB

Takeishi et al. supplementary movie 2

Rolling RBC for Ca = 0.05 and λ = 5.0. The initial orientation angle is Ψ0 = rand. (at least Ψ0 ≠ 0 or ≠ π/2).

Download Takeishi et al. supplementary movie 2(Video)
Video 3 MB

Takeishi et al. supplementary movie 3

RBC with complex deformed shape for Ca = 1.2 and λ = 5.0. The initial orientation angle is Ψ0 = π/4.

Download Takeishi et al. supplementary movie 3(Video)
Video 9 MB

Takeishi et al. supplementary movie 4

RBC with complex deformed shape for Ca = 0.8 and λ = 5.0. The initial orientation angle is Ψ0 = π/4.

Download Takeishi et al. supplementary movie 4(Video)
Video 8.9 MB

Takeishi et al. supplementary movie 5

RBC with periodic motion (kayaking motion) for Ca = 0.2 and λ = 0.1. The initial orientation angle is Ψ0 = π/4.

Download Takeishi et al. supplementary movie 5(Video)
Video 4.3 MB

Takeishi et al. supplementary movie 6

Semi-dilute suspension (φ = 0.05) of RBCs for Ca = 0.05 and λ = 5.0.

Download Takeishi et al. supplementary movie 6(Video)
Video 4.7 MB

Takeishi et al. supplementary movie 7

Dense suspension (φ = 0.41) of RBCs for Ca = 0.05 and λ = 5.0.

Download Takeishi et al. supplementary movie 7(Video)
Video 7.6 MB

Takeishi et al. supplementary movie 8

Semi-dilute suspension (φ = 0.05) of RBCs for Ca = 0.8 and λ = 5.0.

Download Takeishi et al. supplementary movie 8(Video)
Video 4.9 MB

Takeishi et al. supplementary movie 9

Dense suspension (φ = 0.41) of RBCs for Ca = 0.8 and λ = 5.0.

Download Takeishi et al. supplementary movie 9(Video)
Video 7.6 MB