Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-01T12:36:45.688Z Has data issue: false hasContentIssue false
  • English
  • Français

Gyrotactic bioconvection at pycnoclines

Published online by Cambridge University Press:  26 September 2013

A. Karimi  and
A. M. Ardekani
A. Karimi*
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Notre Dame, Notre Dame, IN 46556, USA
A. M. Ardekani
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Notre Dame, Notre Dame, IN 46556, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Bioconvection is an important phenomenon in aquatic environments, affecting the spatial distribution of motile micro-organisms and enhancing mixing within the fluid. However, stratification arising from thermal or solutal gradients can play a pivotal role in suppressing the bioconvective flows, leading to the aggregation of micro-organisms and growth of their patchiness. We investigate the combined effects by considering gyrotactic motility where the up-swimming cells are directed by the balance of the viscous and gravitational torques. To study this system, we employ a continuum model consisting of Navier–Stokes equations with the Boussinesq approximation coupled with two conservation equations for the concentration of cells and stratification agent. We present a linear stability analysis to determine the onset of bioconvection for different flow parameters. Also, using large-scale numerical simulations, we explore different regimes of the flow by varying the corresponding boundary conditions and dimensionless variables such as Rayleigh number and Lewis number (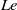$\mathit{Le}$) and we show that the cell distribution can be characterized using the ratio of the buoyancy forces as the determinant parameter when 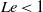$\mathit{Le}\lt 1$ and the boundaries are insulated. But, in thermally stratified fluids corresponding to 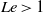$\mathit{Le}\gt 1$, temperature gradients are demonstrated to have little impact on the bioconvective plumes provided that the walls are thermally insulated. In addition, we analyse the dynamical behaviour of the system in the case of persistent pycnoclines corresponding to constant salinity boundary conditions and we discuss the associated inhibition threshold of bioconvection in the light of the stability of linearized solutions.

JFM classification

Biological Fluid Dynamics: Bioconvection Convection: Buoyancy-driven instability Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 733 , 25 October 2013 , pp. 245 - 267
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alldredge, A. L. & Gotschalk, C. C. 1989 Direct observations of the mass flocculation of diatom blooms: characteristics, settling velocities and formation of diatom aggregates. Deep-Sea Res. A 36 (2), 159–171.Google Scholar
Ardekani, A. M. & Stocker, R. 2010 Stratlets: low Reynolds number point-force solutions in a stratified fluid. Phys. Rev. Lett. 105 (8), 084502.Google Scholar
Ascher, U. M & Petzold, L. R. 1998 Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations. Society for Industrial and Applied Mathematics.Google Scholar
Bearon, R. N., Bees, M. A. & Croze, O. A. 2012 Biased swimming cells do not disperse in pipes as tracers: a population model based on microscale behaviour. Phys. Fluids 24, 121902.Google Scholar
Bearon, R. N. & Grunbaum, D. 2006 Bioconvection in a stratified environment: experiments and theory. Phys. Fluids 18 (12), 127102.CrossRefGoogle Scholar
Bearon, R. N., Hazel, A. L. & Thorn, G. J. 2011 The spatial distribution of gyrotactic swimming micro-organisms in laminar flow fields. J. Fluid Mech. 680, 602–635.Google Scholar
Bees, M. A. & Hill, N. A. 1997 Wavelengths of bioconvection patterns. J. Expl Biol. 200, 1515–1526.Google Scholar
Bergström, B. & Strömberg, J. O. 1997 Behavioural differences in relation to pycnoclines during vertical migration of the euphausiids Meganyctiphanes norvegica (m. sars) and Thysanoessa raschii (m. sars). J. Plankton Res. 19 (2), 255–261.CrossRefGoogle Scholar
Berke, A. P., Turner, L., Berg, H. C. & Lauga, E. 2008 Hydrodynamic attraction of swimming microorganisms by surfaces. Phys. Rev. Lett. 101, 038102.Google Scholar
Chiam, K. H., Cross, M. C., Greenside, H. S. & Fischer, P. F. 2005 Enhanced tracer transport by the spiral defect chaos state of a convecting fluid. Phys. Rev. E 71 (3), 036205.Google Scholar
Doostmohammadi, A., Stocker, R. & Ardekani, A. M. 2012 Low-Reynolds-number swimming at pycnoclines. Proc. Natl Acad. Sci. USA 109 (10), 3856–3861.CrossRefGoogle ScholarPubMed
Fischer, P. F. 1997 An overlapping Schwarz method for spectral element solution of the incompressible Navier–Stokes equations. J. Comput. Phys. 133, 84–101.Google Scholar
Ghorai, S. & Hill, N. A. 2000 Periodic arrays of gyrotactic plumes in bioconvection. Phys. Fluids 12 (1), 5–22.Google Scholar
Ghorai, S. & Hill, N. A. 2007 Gyrotactic bioconvection in three dimensions. Phys. Fluids 19 (5), 054107.Google Scholar
Ghorai, S., Panda, M. K. & Hill, N. A. 2010 Bioconvection in a suspension of isotropically scattering phototactic algae. Phys. Fluids 22, 071901.CrossRefGoogle Scholar
Hershberger, P. K., Rensel, J. E., Matter, A. L. & Taub, F. B. 1997 Vertical distribution of the chloromonad flagellate Heterosigma carterae in columns: implications for bloom development. Can. J. Fish. Aquat. Sci. 54 (10), 2228–2234.Google Scholar
Hill, N. A. & Bees, M. A. 2002 Taylor dispersion of gyrotactic swimming micro-organisms in a linear flow. Phys. Fluids 14, 2598–2605.Google Scholar
Hill, N. A. & Pedley, T. J. 2005 Bioconvection. Fluid Dyn. Res. 37 (1–2), 1–20.Google Scholar
Hill, N. A., Pedley, T. J. & Kessler, J. O. 1989 Growth of bioconvection patterns in a suspension of gyrotactic micro-organisms in a layer of finite depth. J. Fluid Mech. 208, 509–543.Google Scholar
Hillesdon, A. J. & Pedley, T. J. 1996 Bioconvection in suspensions of oxytactic bacteria: linear theory. J. Fluid Mech. 324, 223–259.Google Scholar
Hillesdon, A. J., Pedley, T. J. & Kessler, J. O. 1995 The development of concentration gradients in a suspension of chemotactic bacteria. Bull. Math. Biol. 57, 299–344.Google Scholar
Hopkins, M. M. & Fauci, L. J. 2002 A computational model of the collective fluid dynamics of motile micro-organisms. J. Fluid Mech. 455, 149–174.Google Scholar
Huppert, H. E. & Turner, J. S. 1981 Double-diffusive convection. J. Fluid Mech. 106, 299–329.Google Scholar
Jephson, T. & Carlsson, P. 2009 Species- and stratification-dependent diel vertical migration behaviour of three dinoflagellate species in a laboratory study. J. Plankton Res. 31 (11), 1353–1362.Google Scholar
Karimi, A. 2012 Gaining new insights into spatiotemporal chaos with numerics. PhD thesis, Virginia Polytechnic Institute and State University.Google Scholar
Karimi, A. & Paul, M. R. 2012 Quantifying spatiotemporal chaos in Rayleigh–Bénard convection. Phys. Rev. E 85 (4), 046201.Google Scholar
Karimi, A. & Paul, M. R. 2013 Bioconvection in spatially extended domains. Phys. Rev. E 87 (5), 053016.CrossRefGoogle ScholarPubMed
Kessler, J. O. 1984 Gyrotactic buoyant convection and spontaneous pattern formation in algal cell cultures. In Non-Equilibrium Cooperative Phenomena in Physics and Related Fields (ed. Velarde, M. G.), pp. 241–248. Plenum.Google Scholar
Kessler, J. O. 1985 Hydrodynamic focusing of motile algal cells. Nature 313 (5999), 218–220.Google Scholar
Kessler, J. O. 1986 Individual and collective fluid-dynamics of swimming cells. J. Fluid Mech. 173, 191–205.CrossRefGoogle Scholar
Loefer, J. B. & Mefferd, R. B. 1952 Concerning pattern formation by free-swimming microorganisms. Am. Nat. 86 (830), 325–329.Google Scholar
Manela, A. & Frankel, I. 2003 Generalized taylor dispersion in suspensions of gyrotactic swimming micro-organisms. J. Fluid Mech. 490, 99–127.Google Scholar
Mendelson, N. H. 1999 Bacillus subtilis macrofibres, colonies and bioconvection patterns use different strategies to achieve multicellular organization. Environ. Microbiol. 1 (6), 471–477.Google Scholar
Paul, M. R., Chiam, K. H., Cross, M. C., Fischer, P. F. & Greenside, H. S. 2003 Pattern formation and dynamics in Rayleigh–Bénard convection: numerical simulations of experimentally realistic geometries. Physica D 184, 114–126.Google Scholar
Paul, M. R., Cross, M. C., Fischer, P. F. & Greenside, H. S. 2001 Power-law behaviour of power spectra in low Prandtl number Rayleigh–Bénard convection. Phys. Rev. Lett. 87 (15), 154501.Google Scholar
Pedley, T. J., Hill, N. A. & Kessler, J. O. 1988 The growth of bioconvection patterns in a uniform suspension of gyrotactic microorganisms. J. Fluid Mech. 195, 223–237.Google Scholar
Pedley, T. J. & Kessler, J. O. 1987 The orientation of spheroidal microorganisms swimming in a flow field. Proc. R. Soc. Lond. B 231 (1262), 47–70.Google Scholar
Pedley, T. J. & Kessler, J. O. 1990 A new continuum model for suspensions of gyrotactic microorganisms. J. Fluid Mech. 212, 155–182.Google Scholar
Pedley, T. J. & Kessler, J. O. 1992 Hydrodynamic phenomena in suspensions of swimming microorganisms. Annu. Rev. Fluid Mech. 24, 313–358.CrossRefGoogle Scholar
Plesset, M. S. & Winet, H. 1974 Bioconvection patterns in swimming microorganism cultures as an example of Rayleigh–Taylor instability. Nature 248 (5447), 441–443.Google Scholar
Saintillan, D. & Shelley, M. J. 2008 Instabilities and pattern formation in active particle suspensions: kinetic theory and continuum simulations. Phys. Rev. Lett. 100, 178103.Google Scholar
Sherman, B. S., Webster, I. T., Jones, G. J. & Oliver, R. L. 1998 Transitions between Aulacoseira and Anabaena dominance in a turbid river weir pool. Limnol. Oceanogr. 43 (8), 1902–1915.CrossRefGoogle Scholar
Smayda, T. J. 1997 Harmful algal blooms: their ecophysiology and general relevance to phytoplankton blooms in the sea. Limnol. Oceanogr. 42 (5), 1137–1153.Google Scholar
Thorn, G. J. & Bearon, R. N. 2010 Transport of spherical gyrotactic organisms in general three-dimensional flow fields. Phys. Fluids 22 (4), 041902.Google Scholar
Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Turner, J. S. 1985 Multicomponent convection. Annu. Rev. Fluid Mech. 17, 11–44.Google Scholar
Wille, J. J. & Ehret, C. F. 1968 Circadian rhythm of pattern formation in populations of a free-swimming organism, Tetrahymena . J. Eukaryot. Microbiol. 15 (4), 789–792.Google Scholar
Yamamoto, Y., Okayama, T., Sato, K. & Takaoki, T. 1992 Relation of pattern-formation to external conditions in the flagellate, Chlamydomonas-Reinhardtii . Eur. J. Protistol. 28 (4), 415–420.Google Scholar
Yamazaki, H. & Squires, K. D. 1996 Comparison of oceanic turbulence and copepod swimming. Mar. Ecol. Prog. Ser. 14 (1), 299–301.Google Scholar

Karimi and A. M. Ardekani supplementary movies

Plume dynamics represented as the time evolution of isosurfaces of cell concentration. The background fluid is homogenous and the domain aspect ratios are Γh=Γv=1.

Download Karimi and A. M. Ardekani supplementary movies(Video)
Video 1.4 MB

Karimi and A. M. Ardekani supplementary movies

Temporal evolution of isosurfaces of cell concentration and vertical distribution of salinity. The domain aspect ratios are Γh=1 and Γv=5 with parameters Le=0.03 and Rs =104.

Download Karimi and A. M. Ardekani supplementary movies(Video)
Video 4.3 MB