Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-01T00:36:56.977Z Has data issue: false hasContentIssue false
  • English
  • Français

Global linear stability analysis of the wake and path of buoyancy-driven disks and thin cylinders

Published online by Cambridge University Press:  05 January 2014

Joël Tchoufag ,
David Fabre  and
Jacques Magnaudet
Joël Tchoufag
Affiliation:
Université de Toulouse, INPT, UPS, IMFT (Institut de Mécanique des Fluides de Toulouse), Allée Camille Soula, F-31400 Toulouse, France
David Fabre
Affiliation:
Université de Toulouse, INPT, UPS, IMFT (Institut de Mécanique des Fluides de Toulouse), Allée Camille Soula, F-31400 Toulouse, France
Jacques Magnaudet*
Affiliation:
Université de Toulouse, INPT, UPS, IMFT (Institut de Mécanique des Fluides de Toulouse), Allée Camille Soula, F-31400 Toulouse, France CNRS, IMFT, F-31400 Toulouse, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The stability of the vertical path of a gravity- or buoyancy-driven disk of arbitrary thickness falling or rising in a viscous fluid, recently studied through direct numerical simulation by Auguste, Magnaudet & Fabre (J. Fluid Mech., vol. 719, 2013, pp. 388–405), is investigated numerically in the framework of global linear stability. The disk is allowed to translate and rotate arbitrarily and the stability analysis is carried out on the fully coupled system obtained by linearizing the Navier–Stokes equations for the fluid and Newton’s equations for the body. Three disks with different diameter-to-thickness ratios are considered: one is assumed to be infinitely thin, the other two are selected as archetypes of thin and thick cylindrical bodies, respectively. The analysis spans the whole range of body-to-fluid inertia ratios and considers Reynolds numbers (based on the fall/rise velocity and body diameter) up to 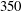$350$. It reveals that four unstable modes with an azimuthal wavenumber $m=\pm 1$ exist in each case. Three of these modes result from a Hopf bifurcation while the fourth is associated with a stationary bifurcation. Varying the body-to-fluid inertia ratio yields rich and complex stability diagrams with several branch crossings resulting in frequency jumps; destabilization/restabilization sequences are also found to take place in some subdomains. The spatial structure of the unstable modes is also examined. Analyzing differences between their real and imaginary parts (which virtually correspond to two different instants of time in the dynamics of a given mode) allows us to assess qualitatively the strength of the mutual coupling between the body and fluid. Qualitative and quantitative differences between present predictions and known results for wake instability past a fixed disk enlighten the fact that the first non-vertical regimes generally result from an intrinsic coupling between the body and fluid and not merely from the instability of the sole wake.

JFM classification

Aerodynamics: Aerodynamics Instability: Instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 740 , 10 February 2014 , pp. 278 - 311
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alben, S. 2008 An implicit method for coupled flow–body dynamics. J. Comput. Phys. 227, 4912–4933.CrossRefGoogle Scholar
Assemat, P., Fabre, D. & Magnaudet, J. 2012 The onset of unsteadiness of two-dimensional bodies falling or rising freely in a viscous fluid: a linear study. J. Fluid Mech. 690, 173–202.Google Scholar
Auguste, F. 2010 Instabilités de sillage générées derrière un corps solide cylindrique fixe ou mobile dans un fluide visqueux. PhD thesis, Université de Toulouse, Toulouse, France. Available at http://thesesups.ups-tlse.fr/1186/.Google Scholar
Auguste, F., Magnaudet, J. & Fabre, D. 2013 Falling styles of disks. J. Fluid Mech. 719, 388–405.Google Scholar
Chrust, M., Bouchet, G. & Dusek, J. 2013 Numerical simulation of the dynamics of freely falling discs. Phys. Fluids 25, 044102.Google Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Annu. Rev. Fluid Mech. 44, 97–121.CrossRefGoogle Scholar
Fabre, D., Assemat, P. & Magnaudet, J. 2011 A quasi-static approach to the stability of the path of heavy bodies falling within a viscous fluid. J. Fluids Struct. 27, 758–767.CrossRefGoogle Scholar
Fabre, D., Tchoufag, J. & Magnaudet, J. 2012 The steady oblique path of buoyancy-driven disks and spheres. J. Fluid Mech. 707, 24–36.CrossRefGoogle Scholar
Fernandes, P. C., Ern, P., Risso, F. & Magnaudet, J. 2008 Dynamics of axisymmetric bodies rising along a zigzag path. J. Fluid Mech. 606, 209–223.Google Scholar
Fernandes, P. C., Risso, F., Ern, P. & Magnaudet, J. 2007 Oscillatory motion and wake instability of freely-rising axisymmetric bodies. J. Fluid Mech. 573, 479–502.Google Scholar
Field, S. B., Klaus, M., Moore, M. G. & Nori, F. 1997 Chaotic dynamics of falling disks. Nature 388, 252–254.CrossRefGoogle Scholar
Horowitz, M. & Williamson, C. H. K. 2010 The effect of Reynolds number on the dynamics and wakes of freely rising and falling spheres. J. Fluid Mech. 651, 251–294.Google Scholar
Howe, M. S. 1995 On the force and moment on a body in an incompressible fluid, with application to rigid bodies and bubbles at high and low Reynolds numbers. Q. J. Mech. Appl. Maths 48, 401–426.Google Scholar
Jenny, M. & Dusek, J. 2004 Efficient numerical method for the direct numerical simulation of the flow past a single light moving spherical body in transitional regimes. J. Comput. Phys. 194, 215–232.Google Scholar
Jenny, M., Dusek, J. & Bouchet, G. 2004 Instabilities and transition of a sphere falling or ascending freely in a Newtonian fluid. J. Fluid Mech. 508, 201–239.Google Scholar
Magnaudet, J. 2011 A ‘reciprocal’ theorem for the prediction of loads on a body moving in an inhomogeneous flow at arbitrary Reynolds number. J. Fluid Mech. 689, 564–604.CrossRefGoogle Scholar
Meliga, P., Chomaz, J. M. & Sipp, D. 2009a Global mode interaction and pattern selection in the wake of a disk: a weakly nonlinear expansion. J. Fluid Mech. 633, 159–189.Google Scholar
Meliga, P., Chomaz, J. M. & Sipp, D. 2009b Unsteadiness in the wake of disks and spheres: instability, receptivity and control using direct and adjoint global stability analyses. J. Fluids Struct. 25, 601–616.CrossRefGoogle Scholar
Mougin, G. & Magnaudet, J. 2002a The generalized Kirchhoff equations and their application to the interaction between a rigid body and a arbitrary time-dependent viscous flow. Intl J. Multiphase Flow 28, 1837–1851.Google Scholar
Mougin, G. & Magnaudet, J. 2002b Path instability of a rising bubble. Phys. Rev. Lett. 88, 014502.Google Scholar
Natarajan, R. & Acrivos, A. 1993 The instability of the steady flow past spheres and disks. J. Fluid Mech. 254, 323–344.Google Scholar
Prosperetti, A. 2004 Bubbles. Phys. Fluids 16, 1852–1865.Google Scholar
Prosperetti, A., Ohl, C. D., Tijink, A., Mougin, G. & Magnaudet, J. 2003 Leonardo’s paradox (Appendix to ‘The added mass of an expanding bubble’ by C. D. Ohl, A. Tijink and A. Prosperetti). J. Fluid Mech. 482, 271–290.Google Scholar
Roos, F. & Willmarth, W. 1971 Some experimental results on sphere and disk drag. AIAA J. 9, 285–291.Google Scholar
Tchoufag, J., Magnaudet, J. & Fabre, D. 2013 Linear stability and sensitivity of the flow past a fixed oblate spheroidal bubble. Phys. Fluids 25, 054108.Google Scholar
Veldhuis, C. H. J. & Biesheuvel, A. 2007 An experimental study of the regimes of motion of spheres falling or ascending freely in a Newtonian fluid. Intl J. Multiphase Flow 33, 1074–1087.Google Scholar
Willmarth, W., Hawk, N. & Harvey, R. 1964 Steady and unsteady motions and wakes of freely falling disks. Phys. Fluids 7, 197–208.Google Scholar