Published online by Cambridge University Press: 21 July 2016
We report on the dynamics of circular finite-release Boussinesq gravity currents on a uniform slope. The study comprises a series of highly resolved direct numerical simulations for a range of slope angles between  $5^{\circ }$ and
$5^{\circ }$ and 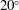 $20^{\circ }$. The simulations were fixed at Reynolds number
$20^{\circ }$. The simulations were fixed at Reynolds number 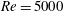 $Re=5000$ for all slopes considered. The temporal evolution of the front is compared to available experimental data. One of the interesting aspects of this study is the detection of a converging flow towards the centre of the gravity current. This converging flow is a result of the finite volume of the release coupled with the presence of a sloping boundary, which results in a second acceleration phase in the front velocity of the current. The details of the dynamics of this second acceleration and the redistribution of material in the current leading to its development will be discussed. These finite-release currents are invariably dominated by the head where most of the mixing and ambient entrainment occurs. We propose a simple method for defining the head of the current from which we extract various properties including the front Froude number and entrainment coefficient. The Froude number is seen to increase with steeper slopes, whereas the entrainment coefficient is observed to be weakly dependent on the bottom slope.
$Re=5000$ for all slopes considered. The temporal evolution of the front is compared to available experimental data. One of the interesting aspects of this study is the detection of a converging flow towards the centre of the gravity current. This converging flow is a result of the finite volume of the release coupled with the presence of a sloping boundary, which results in a second acceleration phase in the front velocity of the current. The details of the dynamics of this second acceleration and the redistribution of material in the current leading to its development will be discussed. These finite-release currents are invariably dominated by the head where most of the mixing and ambient entrainment occurs. We propose a simple method for defining the head of the current from which we extract various properties including the front Froude number and entrainment coefficient. The Froude number is seen to increase with steeper slopes, whereas the entrainment coefficient is observed to be weakly dependent on the bottom slope.