Published online by Cambridge University Press: 24 October 2011
An experimental and numerical study of the evolution of frequency spectra of dispersive focusing wave groups in a two-dimensional wave tank is presented. Investigations of both non-breaking and breaking wave groups are performed. It is found that dispersive focusing is far more than linear superposition, and that it undergoes strongly nonlinear processes. For non-breaking wave groups, as the wave groups propagate spatial evolution of wave frequency spectra, spectral bandwidth, surface elevation skewness, and kurtosis are examined. Nonlinear energy transfer between the above-peak (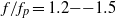 ) and the higher-frequency (
) and the higher-frequency (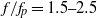 ) regions, with
) regions, with  being the spectral peak frequency, is demonstrated by tracking the energy level of the components in the focusing and defocusing process. Also shown is the nonlinear energy transfer to the lower-frequency components that cannot be detected easily by direct comparisons of the far upstream and downstream measurements. Energy dissipation in the spectral peak region (
being the spectral peak frequency, is demonstrated by tracking the energy level of the components in the focusing and defocusing process. Also shown is the nonlinear energy transfer to the lower-frequency components that cannot be detected easily by direct comparisons of the far upstream and downstream measurements. Energy dissipation in the spectral peak region (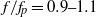 ) and the energy gain in the higher-frequency region (
) and the energy gain in the higher-frequency region (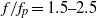 ) are quantified, and exhibit a dependence on the Benjamin–Feir Index (BFI). In the presence of wave breaking, the spectral bandwidth reduces as much as 40 % immediately following breaking and eventually becomes much smaller than its initial level. Energy levels in different frequency regions are examined. It is found that, before wave breaking onset, a large amount of energy is transferred from the above-peak region (
) are quantified, and exhibit a dependence on the Benjamin–Feir Index (BFI). In the presence of wave breaking, the spectral bandwidth reduces as much as 40 % immediately following breaking and eventually becomes much smaller than its initial level. Energy levels in different frequency regions are examined. It is found that, before wave breaking onset, a large amount of energy is transferred from the above-peak region (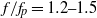 ) to the higher frequencies (
) to the higher frequencies (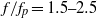 ), where energy is dissipated during the breaking events. It is demonstrated that the energy gain in the lower-frequency region is at least partially due to nonlinear energy transfer prior to wave breaking and that wave breaking may not necessarily increase the energy in this region. Complementary numerical studies for breaking waves are conducted using an eddy viscosity model previously developed by the current authors. It is demonstrated that the predicted spectral change after breaking agrees well with the experimental measurements.
), where energy is dissipated during the breaking events. It is demonstrated that the energy gain in the lower-frequency region is at least partially due to nonlinear energy transfer prior to wave breaking and that wave breaking may not necessarily increase the energy in this region. Complementary numerical studies for breaking waves are conducted using an eddy viscosity model previously developed by the current authors. It is demonstrated that the predicted spectral change after breaking agrees well with the experimental measurements.