Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-21T14:46:52.810Z Has data issue: false hasContentIssue false
  • English
  • Français

Force and torque acting on particles in a transitionally rough open-channel flow

Published online by Cambridge University Press:  13 September 2011

Clemens Chan-Braun ,
Manuel García-Villalba  and
Markus Uhlmann
Clemens Chan-Braun*
Affiliation:
Institute for Hydromechanics, Karlsruhe Institute of Technology, 76131 Karlsruhe, Germany
Manuel García-Villalba
Affiliation:
Institute for Hydromechanics, Karlsruhe Institute of Technology, 76131 Karlsruhe, Germany
Markus Uhlmann
Affiliation:
Institute for Hydromechanics, Karlsruhe Institute of Technology, 76131 Karlsruhe, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

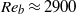Direct numerical simulation of open channel flow over a geometrically rough wall has been performed at a bulk Reynolds number of . The wall consisted of a layer of spheres in a square arrangement. Two cases have been considered. In the first case the spheres are small (with diameter equivalent to 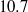wall units) and the limit of the hydraulically smooth flow regime is approached. In the second case the spheres are more than three times larger ( 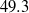wall units) and the flow is in the transitionally rough flow regime. Special emphasis is given to the characterisation of the force and torque acting on a particle due to the turbulent flow. It is found that in both cases the mean drag, lift and spanwise torque are to a large extent produced at the top region of the particle surface. The intensity of the particle force fluctuations is significantly larger in the large-sphere case, while the trend differs for the fluctuations of the individual components of the torque. A simplified model is used to show that the torque fluctuations might be explained by the spheres acting as a filter with respect to the size of the flow scales which can effectively generate torque fluctuations. Fluctuations of both force and torque are found to exhibit strongly non-Gaussian probability density functions with particularly long tails, an effect which is more pronounced in the small-sphere case. Some implications of the present results for sediment erosion are briefly discussed.

JFM classification

Geophysical and Geological Flows: Sediment transport Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 684 , 10 October 2011 , pp. 441 - 474
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Auton, T. 1987 The lift force on a spherical body in a rotational flow. J. Fluid Mech. 183, 199–218.CrossRefGoogle Scholar
2. Auton, T. R., Hunt, J. C. R. & Prud’homme, M. 1988 The force on a body in inviscid unsteady non-uniform rotational flow. J. Fluid Mech. 197, 241–257.CrossRefGoogle Scholar
3. Bagchi, P. & Balachandar, S. 2002 Steady planar straining flow past a rigid sphere at moderate Reynolds number. J. Fluid Mech. 466, 365–407.CrossRefGoogle Scholar
4. Bagchi, P. & Balachandar, S. 2003 Effect of turbulence on the drag and lift of a particle. Phys. Fluids 15 (11), 3496–3513.CrossRefGoogle Scholar
5. Bagchi, P. & Balachandar, S. 2004 Response of the wake of an isolated particle to an isotropic turbulent flow. J. Fluid Mech. 518, 95–123.CrossRefGoogle Scholar
6. Bayazit, M. 1983 Flow structure and sediment transport mechanics in steep channels. In Mechanics of Sediment Transport, Proc. EUROMECH 156 Colloquium (ed. Sumer, B. M. & Müller, A. ), pp. 197–206. A.A. Balkema.Google Scholar
7. Bradshaw, P. 2000 A note on ‘critical roughness height’ and ‘transitional roughness’. Phys. Fluids 12 (6), 1611–1614.CrossRefGoogle Scholar
8. Cameron, S. M. 2006 Near-boundary flow structure and particle entrainment. PhD thesis, University of Auckland.Google Scholar
9. Colebrook, C. F. 1939 Turbulent flow in pipes with particular reference to the transition region between the smooth- and rough-pipe laws. J. Inst. Civil Engrs 11, 133–156.CrossRefGoogle Scholar
10. Detert, M., Nikora, V. & Jirka, G. H. 2010a Synoptic velocity and pressure fields at the water-sediment interface of streambeds. J. Fluid Mech. 660, 55–86.CrossRefGoogle Scholar
11. Detert, M., Weitbrecht, V. & Jirka, G. H. 2010b Laboratory measurements on turbulent pressure fluctuations in and above gravel beds. J. Hydraul. Engng 1, 126–126.Google Scholar
12. Dittrich, A. 1998 Wechselwirkung Morphologie/Strömung naturnaher Fließgewässer. Habilitation, Univ. Karlsruhe (TH).Google Scholar
13. Einstein, H. A. & El-Samni, E.-S. A. 1949 Hydrodynamic forces on a rough wall. Rev. Mod. Phys. 21 (3), 520–524.CrossRefGoogle Scholar
14. Fadlun, E. A., Verzicco, R., Orlandi, P. & Mohd-Yusof, J. 2000 Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations. J. Comput. Phys. 161 (1), 35–60.CrossRefGoogle Scholar
15. Fenton, J. & Abbott, J. 1977 Initial movement of grains on a stream bed: the effect of relative protrusion. Proc. R. Soc. Lond. A 352 (1671), 523–537.Google Scholar
16. Flores, O. & Jiménez, J. 2006 Effect of wall-boundary disturbances on turbulent channel flows. J. Fluid Mech. 566, 357–376.CrossRefGoogle Scholar
17. García, M. H. 2008 Sedimentation Engineering: Processes, Measurements, Modeling, and Practice. American Soc. Civil Eng. (ASCE), ASCE Manual of Practice 110.CrossRefGoogle Scholar
18. Grass, A. J., Stuart, R. J. & Mansour-Tehrani, M. 1991 Vortical structures and coherent motion in turbulent flow over smooth and rough boundaries. Phil. Trans. R. Soc. Lond. A 336, 36–65.Google Scholar
19. Hall, D. 1988 Measurements of the mean force on a particle near a boundary in turbulent flow. J. Fluid Mech. 187, 451–466.CrossRefGoogle Scholar
20. Hofland, B. 2005 Rock and roll, turbulence-induced damage to granular bed protections. PhD thesis, Tech. Univ. Delft.Google Scholar
21. Hofland, B. & Battjes, J. 2006 Probability density functions of instantaneous drag forces and shear stresses on a bed. J. Hydraul. Engng 132 (11), 1169–1175.CrossRefGoogle Scholar
22. Hofland, B., Battjes, J. & Booij, R. 2005 Measurement of fluctuating pressures on coarse bed material. J. Hydraul. Engng 131 (9), 770–781.CrossRefGoogle Scholar
23. Jackson, P. S. 1981 On the displacement height in the logarithmic velocity profile. J. Fluid Mech. 111, 15–25.CrossRefGoogle Scholar
24. Jiménez, J. 2004 Turbulent flow over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.CrossRefGoogle Scholar
25. Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.CrossRefGoogle Scholar
26. Kim, J. 1989 On the structure of pressure fluctuations in simulated turbulent channel flow. J. Fluid Mech. 205, 421–451.CrossRefGoogle Scholar
27. Kim, I., Elghobashi, S. & Sirignano, W. A. 1993 Three-dimensional flow over two spheres placed side by side. J. Fluid Mech. 246, 465–488.CrossRefGoogle Scholar
28. Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
29. King, M. R. & Leighton, D. T. J. 1997 Measurement of the inertial lift on a moving sphere in contact with a plane wall in a shear flow. Phys. Fluids 9 (5), 1248–1255.CrossRefGoogle Scholar
30. Krishnan, G. P. & Leighton, D. T. J. 1995 Inertial lift on a moving sphere in contact with a plane wall in a shear flow. Phys. Fluids 7 (11), 2538–2545.CrossRefGoogle Scholar
31. Lee, H. & Balachandar, S. 2010 Drag and lift forces on a spherical particle moving on a wall in a shear flow at finite Re . J. Fluid Mech. 657, 89–125.CrossRefGoogle Scholar
32. Lee, S.-H. & Sung, H. J. 2007 Direct numerical simulation of the turbulent boundary layer over a rod-roughened wall. J. Fluid Mech. 584, 125–146.CrossRefGoogle Scholar
33. Lee, J. H., Sung, H. J. & Krogstad, P.-A. 2011 Direct numerical simulation of the turbulent boundary layer over a cube-roughened wall. J. Fluid Mech. 669, 397–431.CrossRefGoogle Scholar
34. Leonardi, S., Orlandi, P. & Antonia, R. A. 2007 Properties of d- and k-type roughness in a turbulent channel flow. Phys. Fluids 19 (12), 125101.CrossRefGoogle Scholar
35. Leonardi, S., Orlandi, P., Smalley, R. J., Djenidi, L. & Antonia, R. A. 2003 Direct numerical simulations of turbulent channel flow with transverse square bars on one wall. J. Fluid Mech. 491, 229–238.CrossRefGoogle Scholar
36. Ligrani, P. M. & Moffat, R. J. 1986 Structure of transitionally rough and fully rough turbulent boundary layers. J. Fluid Mech. 162, 69–98.CrossRefGoogle Scholar
37. Lucci, F., Ferrante, A. & Elghobashi, S. 2010 Modulation of isotropic turbulence by particles of Taylor length-scale size. J. Fluid Mech. 650, 5–55.CrossRefGoogle Scholar
38. Manes, C., Pokrajac, D. & McEwan, I. 2007 Double-averaged open-channel flows with small relative submergence. J. Hydraul. Engng 133 (8), 896–904.CrossRefGoogle Scholar
39. Manes, C., Pokrajac, D., Nikora, V. I., Ridolfi, L. & Poggi, D. 2011 Turbulent friction in flows over permeable walls. Geophys. Res. Lett. 38 (3), L03402.CrossRefGoogle Scholar
40. Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22 (6), 065103.CrossRefGoogle Scholar
41. Mollinger, A. & Nieuwstadt, F. 1996 Measurement of the lift force on a particle fixed to the wall in the viscous sublayer of a fully developed turbulent boundary layer. J. Fluid Mech. 316, 285–306.CrossRefGoogle Scholar
42. Muñoz Goma, R. J. & Gelhar, L. W. 1968 Turbulent pipe flow with rough and porous walls. Int. Rep. 109. Hydrodyn. Lab., Dep. Civil Eng., MIT.Google Scholar
43. Muthanna, C., Nieuwstadt, F. T. M. & Hunt, J. C. R. 2005 Measurement of the aerodynamic forces on a small particle attached to a wall. Exp. Fluids 39, 455–463.CrossRefGoogle Scholar
44. Nakagawa, H. & Nezu, I. 1977 Prediction of the contributions to the Reynolds stress from bursting events in open-channel flows. J. Fluid Mech. 80 (01), 99–128.CrossRefGoogle Scholar
45. Nezu, I. & Nakagawa, H. 1993 Turbulence in Open-Channel Flows. IAHR/AIRH Monograph Series , Balkema.Google Scholar
46. Nikora, V., McEwan, I., McLean, S., Coleman, S., Pokrajac, D. & Walters, R. 2007 Double-averaging concept for rough-bed open-channel and overland flows: theoretical background. J. Hydraul. Engng 133 (8), 873–883.CrossRefGoogle Scholar
47. Nikora, V. I., Goring, D. G., MacEwan, I. & Griffiths, G. 2001 Spatially averaged open-channel flow over rough bed. J. Hydraul. Engng 127 (2), 123–133.CrossRefGoogle Scholar
48. Nikuradse, J. 1933 Strömungsgesetze in rauhen Rohren. VDI-Forschungsheft 361, (translation 1950, Laws of flow in rough pipes. NACA TM 1292).Google Scholar
49. Orlandi, P. & Leonardi, S. 2008 Direct numerical simulation of three-dimensional turbulent rough channels: parameterization and flow physics. J. Fluid Mech. 606, 399–415.CrossRefGoogle Scholar
50. Orlandi, P., Leonardi, S., Tuzi, R. & Antonia, R. A. 2003 Direct numerical simulation of turbulent channel flow with wall velocity disturbances. Phys. Fluids 15 (12), 3587–3601.CrossRefGoogle Scholar
51. Papanicolaou, A., Diplas, P., Evaggelopoulos, N. & Fotopoulos, S. 2002 Stochastic incipient motion criterion for spheres under various packing conditions. J. Hydraul. Engng 128 (4), 369–380.CrossRefGoogle Scholar
52. Peskin, C. S. 1972 Flow patterns around heart valves: a digital computer method for solving the equation of motion. PhD thesis, Albert Einstein College of Medicine.CrossRefGoogle Scholar
53. Peskin, C. S. 2002 The immersed boundary method. Acta Numerica 11, 479–517.CrossRefGoogle Scholar
54. Pimenta, M. M., Moffat, R. J. & Kays, W. M. 1975 The turbulent boundary layer: an experimental study of the transport of momentum and heat with the effect of roughness. Int. Rep. HMT-21. Dep. Mech. Eng. Stanford Univ.Google Scholar
55. Poggy, D., Porporato, A. & Ridolfi, L. 2003 Analysis of the small-scale structure of turbulence on smooth and rough walls. Phys. Fluids 15 (1), 35–46.CrossRefGoogle Scholar
56. Pokrajac, D., Finnigan, J., Manes, C., McEwan, I. & Nikora, V. 2006 On the definition of shear velocity in rough bed open-channel flows. In River Flow 2006 (ed. Ferreiara, R., Alves, E., Leal, J. & Cardoso, A. ). A.A. Balkema.Google Scholar
57. Pokrajac, D. & Manes, C. 2009 Velocity measurements of a free-surface turbulent flow penetrating a porous medium composed of uniform-size spheres. Trans. Porous Med. 78, 367–383.CrossRefGoogle Scholar
58. Pope, S. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
59. Raupach, M. R., Antonia, R. A. & Rajagopalan, S. 1991 Rough-wall turbulent boundary layers. Appl. Mech. Rev. 44 (1), 1–25.CrossRefGoogle Scholar
60. van Rijn, L. C. 1993 Principles of Sediment Transport in Rivers, Estuaries, and Costal Seas. Aqua Publications.Google Scholar
61. Roma, A., Peskin, C. & Berger, M. 1999 An adaptive version of the immersed boundary method. J. Comput. Phys. 153 (2), 509–534.CrossRefGoogle Scholar
62. Saffman, P. G. 1965 The lift on a small sphere in a slow shear flow. J. Fluid Mech. 22 (2), 385–400.CrossRefGoogle Scholar
63. Schlichting, H. 1936 Experimentelle Untersuchungen zum Rauhigkeitsprobem. Ing.-Arch. 7, 1–34.CrossRefGoogle Scholar
64. Schlichting, H. 1965 Grenzschicht-Theorie, 5th edn. G. Braun.Google Scholar
65. Shields, A. 1936 Anwendung der Ähnlichkeitsmechanik und der Turbulenzforschung auf die Geschiebebewegung. Mitteilungen der Versuchsanstalt für Wasserbau und Schiffbau (Berlin) 26.Google Scholar
66. Shockling, M. A., Allen, J. J. & Smits, A. J. 2006 Roughness effects in turbulent pipe flow. J. Fluid Mech. 564, 267–285.CrossRefGoogle Scholar
67. Singh, K. M., Sandham, N. D. & Williams, J. J. R. 2007 Numerical simulation of flow over a rough bed. J. Hydraul. Engng 133 (4), 386–398.CrossRefGoogle Scholar
68. Thom, A. S. 1971 Momentum absorption by vegetation. Q. J. R. Meteorol. Soc. 97 (414), 414–428.CrossRefGoogle Scholar
69. Townsend, A. A. 1971 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
70. Uhlmann, M. 2003 New results on the simulation of particulate flows. Tech. Rep. 1038. CIEMAT, ISSN 1135-9420.Google Scholar
71. Uhlmann, M. 2005a An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 209 (2), 448–476.CrossRefGoogle Scholar
72. Uhlmann, M. 2005b An improved fluid–solid coupling method for DNS of particulate flow on a fixed mesh. In Proceedings of 11th Workshop on Two-Phase Flow Predictions (ed. Sommerfeld, M. ). Universität Halle, ISBN 3-86010-767-4.Google Scholar
73. Uhlmann, M. 2006 a Direct numerical simulation of sediment transport in a horizontal channel. Tech. Rep. CIEMAT, ISSN 1135-9420.Google Scholar
74. Uhlmann, M. 2006b Experience with DNS of particulate flow using a variant of the immersed boundary method. In Proceedings of ECCOMAS CFD 2006 (ed. Wesseling, P., Oñate, E. & Périaux, J. ). TU Delft, ISBN 90-9020970-0.Google Scholar
75. Uhlmann, M. 2008 Interface-resolved direct numerical simulation of vertical particulate channel flow in the turbulent regime. Phys. Fluids 20 (5), 053305.CrossRefGoogle Scholar
76. Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123, 402–414.CrossRefGoogle Scholar
77. Willetts, B. B. & Murray, C. G. 1981 Lift exerted on stationary spheres in turbulent flow. J. Fluid Mech. 105, 487–505.CrossRefGoogle Scholar
78. Yun, G., Kim, D. & Choi, H. 2006 Vortical structures behind a sphere at subcritical Reynolds numbers. Phys. Fluids 18 (1), 015102.CrossRefGoogle Scholar
79. Zeng, L., Balachandar, S., Fischer, P. & Najjar, F. 2008 Interactions of a stationary finite-sized particle with wall turbulence. J. Fluid Mech. 594, 271–305.CrossRefGoogle Scholar
80. Zeng, L., Najjar, F., Balachandar, S. & Fischer, P. 2009 Forces on a finite-sized particle located close to a wall in a linear shear flow. Phys. Fluids 21 (3), 033302.CrossRefGoogle Scholar