Article contents
Extension to nonlinear stability theory of the circular Couette flow
Published online by Cambridge University Press: 19 April 2016
Abstract
A nonlinear stability analysis of the viscous circular Couette flow to axisymmetric finite-amplitude perturbations under axial periodic boundary conditions is developed. The analysis is based on investigating the properties of a reduced Arnol’d energy-Casimir function 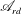 $\mathscr{A}_{rd}$ of Wang (Phys. Fluids, vol. 2, 2009, 084104). A weighted kinetic energy of the perturbation, which has a form of
$\mathscr{A}_{rd}$ of Wang (Phys. Fluids, vol. 2, 2009, 084104). A weighted kinetic energy of the perturbation, which has a form of 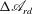 ${\rm\Delta}\mathscr{A}_{rd}$, the difference between the reduced Arnol’d function and its base flow value, is used as a Lyapunov function. We show that all the inviscid flow effects as well as all the viscous-dependent terms that are related to the flow boundaries vanish. The evolution of
${\rm\Delta}\mathscr{A}_{rd}$, the difference between the reduced Arnol’d function and its base flow value, is used as a Lyapunov function. We show that all the inviscid flow effects as well as all the viscous-dependent terms that are related to the flow boundaries vanish. The evolution of 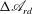 ${\rm\Delta}\mathscr{A}_{rd}$ depends only on the viscous effects of the perturbation’s dynamics inside the flow domain. The requirement for the temporal decay of
${\rm\Delta}\mathscr{A}_{rd}$ depends only on the viscous effects of the perturbation’s dynamics inside the flow domain. The requirement for the temporal decay of 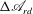 ${\rm\Delta}\mathscr{A}_{rd}$ leads to two novel sufficient conditions for the nonlinear stability of the circular Couette flow in response to axisymmetric perturbations. The linearized version of these conditions for infinitesimally small perturbations recovers the recent linear stability results by Kloosterziel (J. Fluid Mech., vol. 652, 2010, pp. 171–193). By examining the nonlinear stability conditions, we establish a definite operational region of the viscous circular Couette flow that is independent of the fluid viscosity. In this region of operation, the flow is nonlinearly stable in response to perturbations of any size, provided that the initial total circulation function is above a minimum level determined by the operational conditions of the base flow. Comparisons with historical studies show that our results shed light on the experimental measurements of Wendt (Ing.-Arch., vol. 4, 1933, pp. 577–595) and extend the classical nonlinear stability results of Serrin (Arch. Rat. Mech. Anal., vol. 3, 1959, pp. 1–13) and Joseph & Hung (Arch. Rat. Mech. Anal., vol. 44, 1971, pp. 1–22). When the flow is nonlinearly stable and evolves axisymmetrically for all time, then it always decays asymptotically in time to the circular Couette flow determined uniquely by the set-up of the rotating cylinders. Finally, we derive upper-bound estimates on the decay rate of finite-amplitude perturbations for the solid-body rotation flow between two coaxial rotating cylinders and for the circular Couette flow. We demonstrate via numerical simulations that the theoretical upper bound is relevant to the dynamics of various axisymmetric perturbations tested, where it is strictly obeyed. This present study provides new physical insights into a classical flow problem that was studied for many decades.
${\rm\Delta}\mathscr{A}_{rd}$ leads to two novel sufficient conditions for the nonlinear stability of the circular Couette flow in response to axisymmetric perturbations. The linearized version of these conditions for infinitesimally small perturbations recovers the recent linear stability results by Kloosterziel (J. Fluid Mech., vol. 652, 2010, pp. 171–193). By examining the nonlinear stability conditions, we establish a definite operational region of the viscous circular Couette flow that is independent of the fluid viscosity. In this region of operation, the flow is nonlinearly stable in response to perturbations of any size, provided that the initial total circulation function is above a minimum level determined by the operational conditions of the base flow. Comparisons with historical studies show that our results shed light on the experimental measurements of Wendt (Ing.-Arch., vol. 4, 1933, pp. 577–595) and extend the classical nonlinear stability results of Serrin (Arch. Rat. Mech. Anal., vol. 3, 1959, pp. 1–13) and Joseph & Hung (Arch. Rat. Mech. Anal., vol. 44, 1971, pp. 1–22). When the flow is nonlinearly stable and evolves axisymmetrically for all time, then it always decays asymptotically in time to the circular Couette flow determined uniquely by the set-up of the rotating cylinders. Finally, we derive upper-bound estimates on the decay rate of finite-amplitude perturbations for the solid-body rotation flow between two coaxial rotating cylinders and for the circular Couette flow. We demonstrate via numerical simulations that the theoretical upper bound is relevant to the dynamics of various axisymmetric perturbations tested, where it is strictly obeyed. This present study provides new physical insights into a classical flow problem that was studied for many decades.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 1
- Cited by



