No CrossRef data available.
Published online by Cambridge University Press: 10 December 2008
We present a series of laboratory experiments in which a steady stream of air is supplied through a small hole in the wall of a vertical pipe of rectangular cross-section down which there is a steady flux of water. For a range of liquid flow rates, the air forms a steady standing bubble whose nose is attached to the point of air supply. The steady bubble sheds a flux of much smaller air bubbles at its base, located downstream of the air injection point. The minimum liquid speed for which steady standing bubbles develop occurs at a particular Froude number of the liquid flow, Frd = U/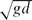 = 0.38, where U is the upstream speed, g the acceleration due to gravity and d the width of the cell. These trapped bubbles are distinct from the freely rising Taylor bubble, in that the Froude number at the nose is variable. Also, on a length scale greater than that influenced by surface tension, we find that the bubble nose asymptotes to a cusp-like shape, with an angle that decreases with Frd. We show that numerical solutions of the potential flow equations replicate the bubble shape and angle of the cusp, which appear independent of the gas flux. We also find that there is a minimum gas flux for which these standing bubbles develop. As the gas flux decreases below this threshold, the standing bubbles become unstable and, instead, a much shorter oscillating bubble develops. This produces a wake which has similarities with that formed downstream of a cylinder in a confined channel, but which also carries bubbles downstream. We also find that with sufficiently small gas flux, no bubble develops. For liquid flow rates smaller than the critical value, Frd < 0.38, we find that the bubbles become unstable and detach from the injection point and rise up the tube.
= 0.38, where U is the upstream speed, g the acceleration due to gravity and d the width of the cell. These trapped bubbles are distinct from the freely rising Taylor bubble, in that the Froude number at the nose is variable. Also, on a length scale greater than that influenced by surface tension, we find that the bubble nose asymptotes to a cusp-like shape, with an angle that decreases with Frd. We show that numerical solutions of the potential flow equations replicate the bubble shape and angle of the cusp, which appear independent of the gas flux. We also find that there is a minimum gas flux for which these standing bubbles develop. As the gas flux decreases below this threshold, the standing bubbles become unstable and, instead, a much shorter oscillating bubble develops. This produces a wake which has similarities with that formed downstream of a cylinder in a confined channel, but which also carries bubbles downstream. We also find that with sufficiently small gas flux, no bubble develops. For liquid flow rates smaller than the critical value, Frd < 0.38, we find that the bubbles become unstable and detach from the injection point and rise up the tube.