Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Klewicki, J.
Philip, J.
Marusic, I.
Chauhan, K.
and
Morrill-Winter, C.
2014.
Self-similarity in the inertial region of wall turbulence.
Physical Review E,
Vol. 90,
Issue. 6,
Lee, Myoungkyu
and
Moser, Robert D.
2015.
Direct numerical simulation of turbulent channel flow up to .
Journal of Fluid Mechanics,
Vol. 774,
Issue. ,
p.
395.
Vallikivi, M.
Hultmark, M.
and
Smits, A. J.
2015.
Turbulent boundary layer statistics at very high Reynolds number.
Journal of Fluid Mechanics,
Vol. 779,
Issue. ,
p.
371.
Klewicki, J.
and
Oberlack, M.
2015.
Finite Reynolds number properties of a turbulent channel flow similarity solution.
Physics of Fluids,
Vol. 27,
Issue. 9,
Hohman, T.C.
Buren, T. Van
Martinelli, L.
and
Smits, A.J.
2015.
Generating an artificially thickened boundary layer to simulate the neutral atmospheric boundary layer.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 145,
Issue. ,
p.
1.
Borisenkov, Youry
Kholmyansky, Michael
Krylov, Slava
Liberzon, Alex
and
Tsinober, Arkady
2015.
Multiarray Micromachined Probe for Turbulence Measurements Assembled of Suspended Hot-Film Sensors.
Journal of Microelectromechanical Systems,
Vol. 24,
Issue. 5,
p.
1503.
Schaefer, John A.
West, Thomas
Hosder, Serhat
Rumsey, Christopher L.
Carlson, Jan-Renee
and
Kleb, William L.
2015.
Uncertainty Quantification of Turbulence Model Closure Coefficients for Transonic Wall-Bounded Flows.
Rodríguez-López, Eduardo
Bruce, Paul J. K.
and
Buxton, Oliver R. H.
2015.
A robust post-processing method to determine skin friction in turbulent boundary layers from the velocity profile.
Experiments in Fluids,
Vol. 56,
Issue. 4,
Ostilla-Mónico, Rodolfo
Verzicco, Roberto
Grossmann, Siegfried
and
Lohse, Detlef
2016.
The near-wall region of highly turbulent Taylor–Couette flow.
Journal of Fluid Mechanics,
Vol. 788,
Issue. ,
p.
95.
Schaefer, John A.
Hosder, Serhat
Mani, Mortaza
Cary, Andrew W.
and
Krakos, Joshua
2016.
The Effect of Grid Topology and Flow Solver on Turbulence Model Closure Coefficient Uncertainties for a Transonic Airfoil.
Örlü, Ramis
Segalini, Antonio
Klewicki, Joseph
and
Alfredsson, P. Henrik
2016.
High-order generalisation of the diagnostic scaling for turbulent boundary layers.
Journal of Turbulence,
Vol. 17,
Issue. 7,
p.
664.
Trettel, Andrew
and
Larsson, Johan
2016.
Mean velocity scaling for compressible wall turbulence with heat transfer.
Physics of Fluids,
Vol. 28,
Issue. 2,
Bailey, S. C. C.
and
Witte, B. M.
2016.
On the universality of local dissipation scales in turbulent channel flow.
Journal of Fluid Mechanics,
Vol. 786,
Issue. ,
p.
234.
Grossmann, Siegfried
and
Lohse, Detlef
2017.
Curvature effects on the velocity profile in turbulent pipe flow.
The European Physical Journal E,
Vol. 40,
Issue. 2,
Mouri, Hideaki
Morinaga, Takeshi
Yagi, Toshimasa
and
Mori, Kazuyasu
2017.
Logarithmic scaling for fluctuations of a scalar concentration in wall turbulence.
Physical Review E,
Vol. 96,
Issue. 6,
Ahn, Junsun
Lee, Jinyoung
and
Sung, Hyung Jin
2017.
Contribution of large-scale motions to the Reynolds shear stress in turbulent pipe flows.
International Journal of Heat and Fluid Flow,
Vol. 66,
Issue. ,
p.
209.
Li, Zhiyong
Zhang, Huaibao
Bailey, Sean C.C.
Hoagg, Jesse B.
and
Martin, Alexandre
2017.
A data-driven adaptive Reynolds-averaged Navier–Stokes k–ω model for turbulent flow.
Journal of Computational Physics,
Vol. 345,
Issue. ,
p.
111.
Ansorge, Cedrick
2017.
Analyses of Turbulence in the Neutrally and Stably Stratified Planetary Boundary Layer.
p.
75.
Richard, G. L.
Rambaud, A.
and
Vila, J. P.
2017.
Consistent equations for open-channel flows in the smooth turbulent regime with shearing effects.
Journal of Fluid Mechanics,
Vol. 831,
Issue. ,
p.
289.
Guo, Junke
2017.
Eddy viscosity and complete log-law for turbulent pipe flow at high Reynolds numbers.
Journal of Hydraulic Research,
Vol. 55,
Issue. 1,
p.
27.
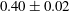 $0.40 \pm 0.02$. A more precise estimate will require improved instrumentation.
$0.40 \pm 0.02$. A more precise estimate will require improved instrumentation.