Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-20T17:58:00.212Z Has data issue: false hasContentIssue false
  • English
  • Français

Enhanced velocity fluctuations in interacting swimmer suspensions

Published online by Cambridge University Press:  25 November 2020

Sankalp Nambiar Open the ORCID record for Sankalp Nambiar [Opens in a new window] ,
Piyush Garg Open the ORCID record for Piyush Garg [Opens in a new window]  and
Ganesh Subramanian Open the ORCID record for Ganesh Subramanian [Opens in a new window]
Sankalp Nambiar
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkuru, Bangalore560064, India
Piyush Garg
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkuru, Bangalore560064, India
Ganesh Subramanian*
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkuru, Bangalore560064, India
*
†Email address of correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

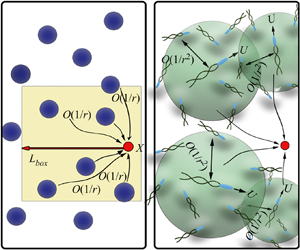
This paper characterizes the nature of velocity fluctuations in swimmer suspensions by determining the fluid velocity variance and the diffusivity of immersed passive tracers in dilute suspensions of hydrodynamically interacting slender microswimmers. The swimmers considered include straight-swimmers whose orientations change only on account of hydrodynamic interactions, and run-and-tumble particles (RTPs) whose orientations change in addition due to tumble events obeying Poisson statistics. In a dilute non-interacting swimmer suspension, the fluid velocity variance is finite and the covariance is short ranged, decaying for distances larger than the swimmer length. In contrast, we show, for a suspension of interacting straight-swimmers, that pair interactions lead to a non-decaying velocity covariance, and a variance that diverges logarithmically with system size. For suspensions of RTPs, the aforementioned divergence is arrested due to tumbling. While the variance remains finite, and the covariance short ranged, for suspensions of interacting rapid tumbling RTPs (short run lengths), the underlying straight-swimmer divergence manifests as a logarithmic increase of the variance with the swimmer run length for persistent RTPs (long run lengths), with a correspondingly long-ranged covariance. The tracer mean squared displacement undergoes an increasingly broad crossover from the ballistic to the diffusive regime for persistent RTPs, with the tracer diffusivity exhibiting a stronger linear increase with the swimmer run length. Our analysis explains the bifurcation of the velocity variance and tracer diffusivities between pusher and puller suspensions, as well as numerous observations of a volume-fraction-dependent crossover time for passive tracer dynamics.

JFM classification

Biological Fluid Dynamics: Micro-organism dynamics Complex Fluids: Suspensions Multiphase and Particle-laden Flows: Particle/fluid flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 907 , 25 January 2021 , A26
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Nordita, KTH Royal Institute of Technology and Stockholm University, Stockholm 10691, Sweden.

References

REFERENCES

Alarcón, F. & Pagonabarraga, I. 2013 Spontaneous aggregation and global polar ordering in squirmer suspensions. J. Mol. Liq. 185, 56–61.CrossRefGoogle Scholar
Alarcón, F., Valeriani, C. & Pagonabarraga, I. 2017 Morphology of clusters of attractive dry and wet self-propelled spherical particle suspensions. Soft Matt. 13 (4), 814–826.CrossRefGoogle ScholarPubMed
Aranson, I. S., Sokolov, A., Kessler, J. O. & Goldstein, R. E. 2007 Model for dynamical coherence in thin films of self-propelled microorganisms. Phys. Rev. E 75 (4), 040901(R).CrossRefGoogle ScholarPubMed
Argun, A., Moradi, A.-R., Pinçe, E., Bagci, G. B., Imparato, A. & Volpe, G. 2016 Non-Boltzmann stationary distributions and nonequilibrium relations in active baths. Phys. Rev. E 94 (6), 062150.CrossRefGoogle ScholarPubMed
Balakrishnan, V. 2008 Elements of Nonequilibrium Statistical Mechanics. Ane Books.Google Scholar
Batchelor, G. K. 1970 Slender-body theory for particles of arbitrary cross-section in Stokes flow. J. Fluid Mech. 44 (3), 419–440.CrossRefGoogle Scholar
Berg, H. C. 2004 E. coli in Motion. Springer.CrossRefGoogle Scholar
Berg, H. C. 1993 Random Walks in Biology. Princeton University Press.Google Scholar
Blake, J. 1973 A finite model for ciliated micro-organisms. Trans. ASME: J. Biomech. 6 (2), 133–140.Google ScholarPubMed
Blake, J. R. 1971 A spherical envelope approach to ciliary propulsion. J. Fluid Mech. 46 (1), 199–208.CrossRefGoogle Scholar
Bárdfalvy, D., Nordanger, H., Nardini, C., Morozov, A. & Stenhammar, J. 2019 Particle-resolved lattice Boltzmann simulations of 3-dimensional active turbulence. Soft Matt. 15 (39), 7747–7756.CrossRefGoogle ScholarPubMed
Caflisch, R. E. & Luke, J. H. C. 1985 Variance in the sedimentation speed of a suspension. Phys. Fluids 28 (3), 759–760.CrossRefGoogle Scholar
Chen, D. T. N., Lau, A. W. C., Hough, L. A., Islam, M. F., Goulian, M., Lubensky, T. C. & Yodh, A. G. 2007 Fluctuations and rheology in active bacterial suspensions. Phys. Rev. Lett. 99 (14), 148302.CrossRefGoogle ScholarPubMed
Clement, E., Lindner, A., Douarche, C. & Auradou, H. 2016 Bacterial suspensions under flow. Eur. Phys. J.: Spec. Top. 225 (11-12), 2389–2406.Google Scholar
Colin, R., Drescher, K. & Sourjik, V. 2019 Chemotactic behaviour of Escherichia coli at high cell density. Nat. Commun. 10, 5329.CrossRefGoogle ScholarPubMed
Delmotte, B., Keaveny, E. E., Climent, E. & Plouraboué, F. 2018 Simulations of Brownian tracer transport in squirmer suspensions. IMA J. Appl. Maths 83 (4), 680–699.CrossRefGoogle Scholar
Dombrowski, C., Cisneros, L., Chatkaew, S., Goldstein, R. E. & Kessler, J. O. 2004 Self-concentration and large-scale coherence in bacterial dynamics. Phys. Rev. Lett. 93 (9), 098103.CrossRefGoogle ScholarPubMed
Dunkel, J., Heidenreich, S., Bär, M. & Goldstein, R. E. 2013 a Minimal continuum theories of structure formation in dense active fluids. New J. Phys. 15 (4), 045016.CrossRefGoogle Scholar
Dunkel, J., Heidenreich, S., Drescher, K., Wensink, H. H., Bär, M. & Goldstein, R. E. 2013 b Fluid dynamics of bacterial turbulence. Phys. Rev. Lett. 110 (22), 228102.CrossRefGoogle ScholarPubMed
Evans, A. A., Ishikawa, T., Yamaguchi, T. & Lauga, E. 2011 Orientational order in concentrated suspensions of spherical microswimmers. Phys. Fluids 23 (11), 111702.CrossRefGoogle Scholar
Felderhof, B. U. 2016 Stokesian swimming of a prolate spheroid at low Reynolds number. Eur. J. Mech. B/Fluids 60, 230–236.CrossRefGoogle Scholar
Fokas, A. S. & Ablowitz, M. J. 2012 Complex Variables: Introduction and Applications. Cambridge University Press.Google Scholar
Gachelin, J., Rousselet, A., Lindner, A. & Clement, E. 2014 Collective motion in an active suspension of Escherichia coli bacteria. New J. Phys. 16 (2), 025003.CrossRefGoogle Scholar
Gakhov, F. D. 1966 Boundary Value Problems. Pergamon Press.CrossRefGoogle Scholar
Gelfand, I. M. & Shilov, G. E. 1964 Generalized Functions, Volume 1, Properties and Operators. AMS Chelsea Publishing.Google Scholar
Goldfriend, T., Diamant, H. & Witten, T. A. 2017 Screening, hyperuniformity, and instability in the sedimentation of irregular objects. Phys. Rev. Lett. 118 (15), 158005.CrossRefGoogle ScholarPubMed
Goldstein, R. E. 2015 Green algae as model organisms for biological fluid dynamics. Annu. Rev. Fluid Mech. 47, 343–375.CrossRefGoogle ScholarPubMed
Gradshteyn, I. M. & Ryzhik, I. S. 1980 Table of Integrals, Series, and Products, vol. 980. Academic Press.Google Scholar
Guasto, J. S, Rusconi, R. & Stocker, R. 2012 Fluid mechanics of planktonic microorganisms. Annu. Rev. Fluid Mech. 44, 373–400.CrossRefGoogle Scholar
Guazzelli, E. & Hinch, J. 2011 Fluctuations and instability in sedimentation. Annu. Rev. Fluid Mech. 43, 97–116.CrossRefGoogle Scholar
Guo, S., Samanta, D., Peng, Y., Xu, X. & Cheng, X. 2018 Symmetric shear banding and swarming vortices in bacterial superfluids. Proc. Natl Acad. Sci. USA 115 (28), 7212–7217.CrossRefGoogle ScholarPubMed
Heidenreich, S., Dunkel, J., Klapp, S. H. L. & Bär, M. 2016 Hydrodynamic length-scale selection in microswimmer suspensions. Phys. Rev. E 94 (2), 020601(R).CrossRefGoogle ScholarPubMed
Hinch, E. J. 1988 Hydrodynamics at low Reynolds numbers: a brief and elementary introduction. In Disorder and Mixing, pp. 43–56. Springer.CrossRefGoogle Scholar
Ishikawa, T. & Pedley, T. J. 2007 a Diffusion of swimming model micro-organisms in a semi-dilute suspension. J. Fluid Mech. 588, 437–462.CrossRefGoogle Scholar
Ishikawa, T. & Pedley, T. J. 2007 b The rheology of a semi-dilute suspension of swimming model micro-organisms. J. Fluid Mech. 588, 399–435.CrossRefGoogle Scholar
Ishikawa, T. & Pedley, T. J. 2008 Coherent structures in monolayers of swimming particles. Phys. Rev. Lett. 100 (8), 088103.CrossRefGoogle ScholarPubMed
Ishikawa, T., Simmonds, M. P. & Pedley, T. J. 2006 Hydrodynamic interaction of two swimming model micro-organisms. J. Fluid Mech. 568, 119–160.CrossRefGoogle Scholar
Jepson, A., Martinez, V. A., Schwarz-Linek, J., Morozov, A. & Poon, W. C. K. 2013 Enhanced diffusion of nonswimmers in a three-dimensional bath of motile bacteria. Phys. Rev. E 88 (4), 041002(R).CrossRefGoogle Scholar
Kanazawa, K., Sano, T. G., Cairoli, A. & Baule, A. 2020 Loopy Lévy flights enhance tracer diffusion in active suspensions. Nature 579, 364–367.CrossRefGoogle ScholarPubMed
Kasyap, T. V., Koch, D. L. & Wu, M. 2014 Hydrodynamic tracer diffusion in suspensions of swimming bacteria. Phys. Fluids (1994-present) 26 (8), 081901.CrossRefGoogle Scholar
Kessler, J. O. 1986 Individual and collective fluid dynamics of swimming cells. J. Fluid Mech. 173, 191–205.CrossRefGoogle Scholar
Kim, M. J. & Breuer, K. S. 2004 Enhanced diffusion due to motile bacteria. Phys. Fluids 16 (9), L78–L81.CrossRefGoogle Scholar
Kim, S. & Karrila, S. J. 1991 Microhydrodynamics: Principles and Selected Applications. Butterworth-Henemann.Google Scholar
Koch, D. L. & Shaqfeh, E. S. G. 1991 Screening in sedimenting suspensions. J. Fluid Mech. 224, 275–303.CrossRefGoogle Scholar
Koch, D. L. & Subramanian, G. 2011 Collective hydrodynamics of swimming microorganisms: living fluids. Annu. Rev. Fluid Mech. 43, 637–659.CrossRefGoogle Scholar
Krishnamurthy, D. & Subramanian, G. 2015 Collective motion in a suspension of micro-swimmers that run-and-tumble and rotary diffuse. J. Fluid Mech. 781, 422–466.CrossRefGoogle Scholar
Krishnamurthy, S., Ghosh, S., Chatterji, D., Ganapathy, R. & Sood, A. K. 2016 A micrometre-sized heat engine operating between bacterial reservoirs. Nat. Phys. 12 (12), 1134.CrossRefGoogle Scholar
Kyoya, K., Matsunaga, D., Imai, Y., Omori, T. & Ishikawa, T. 2015 Shape matters: near-field fluid mechanics dominate the collective motions of ellipsoidal squirmers. Phys. Rev. E 92 (6), 063027.CrossRefGoogle ScholarPubMed
Ladd, A. J. C. 1996 Hydrodynamic screening in sedimenting suspensions of non-Brownian spheres. Phys. Rev. Lett. 76 (8), 1392.CrossRefGoogle ScholarPubMed
Ladd, A. J. C. 1997 Sedimentation of homogeneous suspensions of non-Brownian spheres. Phys. Fluids 9 (3), 491–499.CrossRefGoogle Scholar
Larson, R. G. 2013 Constitutive Equations for Polymer Melts and Solutions: Butterworths Series in Chemical Engineering. Butterworth-Heinemann.Google Scholar
Lauga, E. & Powers, T. R. 2009 The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72, 096601.CrossRefGoogle Scholar
Laxminarsimharao, V., Garg, P. & Subramanian, G. 2020 Concentration banding instability of a sheared bacterial suspension. Journal: J. Fluid Mech. 904, A7.Google Scholar
Leptos, K. C., Guasto, J. S., Gollub, J. P., Pesci, A. I. & Goldstein, R. E. 2009 Dynamics of enhanced tracer diffusion in suspensions of swimming eukaryotic microorganisms. Phys. Rev. Lett. 103 (19), 198103.CrossRefGoogle ScholarPubMed
Levine, A., Ramaswamy, S., Frey, E. & Bruinsma, R. 1998 Screened and unscreened phases in sedimenting suspensions. Phys. Rev. Lett. 81 (26), 5944.CrossRefGoogle Scholar
Lin, Z., Thiffeault, J.-L. & Childress, S. 2011 Stirring by squirmers. J. Fluid Mech. 669, 167–177.CrossRefGoogle Scholar
Liu, Z., Zhang, K. & Cheng, X. 2019 Rheology of bacterial suspensions under confinement. Rheol. Acta 58 (8), 439–451.CrossRefGoogle Scholar
Lopez, H. M., Gachelin, J., Douarche, C., Auradou, H. & Clement, E. 2015 Turning bacteria suspensions into superfluids. Phys. Rev. Lett. 115, 028301.CrossRefGoogle ScholarPubMed
Luke, J. H. C. 2000 Decay of velocity fluctuations in a stably stratified suspension. Phys. Fluids 12 (6), 1619–1621.CrossRefGoogle Scholar
Lushi, E., Wioland, H. & Goldstein, R. E. 2014 Fluid flows created by swimming bacteria drive self-organization in confined suspensions. Proc. Natl Acad. Sci. USA 111 (27), 9733–9738.CrossRefGoogle ScholarPubMed
Mackaplow, M. B. & Shaqfeh, E. S. G. 1996 A numerical study of the rheological properties of suspensions of rigid, non-Brownian fibres. J. Fluid Mech. 329, 155–186.CrossRefGoogle Scholar
Maggi, C., Paoluzzi, M., Pellicciotta, N., Lepore, A., Angelani, L. & Di Leonardo, R. 2014 Generalized energy equipartition in harmonic oscillators driven by active baths. Phys. Rev. Lett. 113 (23), 238303.CrossRefGoogle ScholarPubMed
Marchetti, M. C., Joanny, J.-F., Ramaswamy, S., Liverpool, T. B., Prost, J., Rao, M. & Simha, R. A. 2013 Hydrodynamics of soft active matter. Rev. Mod. Phys. 85 (3), 1143.CrossRefGoogle Scholar
Martinez, V. A., Clément, E., Arlt, J., Douarche, C., Dawson, A., Schwarz-Linek, J., Creppy, A. K., Škultéty, V., Morozov, A. N., Auradou, H., et al. 2020 A combined rheometry and imaging study of viscosity reduction in bacterial suspensions. Proc. Natl Acad. Sci. USA 117 (5), 2326–2331.CrossRefGoogle ScholarPubMed
Mehandia, V. & Nott, P. R. 2008 The collective dynamics of self-propelled particles. J. Fluid Mech. 595, 239–264.CrossRefGoogle Scholar
Nambiar, S., Nott, P. R. & Subramanian, G. 2017 Stress relaxation in a dilute bacterial suspension. J. Fluid Mech. 812, 41–64.CrossRefGoogle Scholar
Nambiar, S., Phanikanth, S., Nott, P. R. & Subramanian, G. 2019 Stress relaxation in a dilute bacterial suspension: the active–passive transition. J. Fluid Mech. 870, 1072–1104.CrossRefGoogle Scholar
Nicolai, H., Herzhaft, B., Hinch, E. J., Oger, L. & Guazzelli, E. 1995 Particle velocity fluctuations and hydrodynamic self-diffusion of sedimenting non-Brownian spheres. Phys. Fluids 7 (1), 12–23.CrossRefGoogle Scholar
Othmer, H. G., Dunbar, S. R. & Alt, W. 1988 Models of dispersal in biological systems. J. Math. Biol. 26 (3), 263–298.CrossRefGoogle ScholarPubMed
Oyama, N., Molina, J. J. & Yamamoto, R. 2017 Do hydrodynamically assisted binary collisions lead to orientational ordering of microswimmers? Eur. Phys. J. E 40 (11), 95.CrossRefGoogle ScholarPubMed
Patteson, A. E., Gopinath, A., Purohit, P. K. & Arratia, P. E. 2016 Particle diffusion in active fluids is non-monotonic in size. Soft Matt. 12 (8), 2365–2372.CrossRefGoogle ScholarPubMed
Pedley, T. J. 2016 Spherical squirmers: models for swimming micro-organisms. IMA J. Appl. Maths 81 (3), 488–521.CrossRefGoogle Scholar
Peng, Y., Lai, L., Tai, Y.-S., Zhang, K., Xu, X. & Cheng, X. 2016 Diffusion of ellipsoids in bacterial suspensions. Phys. Rev. Lett. 116 (6), 068303.CrossRefGoogle ScholarPubMed
Poehnl, R., Popescu, M. N. & Uspal, W. E. 2020 Axisymmetric spheroidal squirmers and self-diffusiophoretic particles. J. Phys.: Condens. Matter 32 (16), 164001.Google Scholar
Pushkin, D. O. & Yeomans, J. M. 2014 Stirring by swimmers in confined microenvironments. J. Stat. Mech. 2014 (4), P04030.CrossRefGoogle Scholar
Qian, Y., Kramer, P. R. & Underhill, P. T. 2017 Stochastic kinetic theory for collective behavior of hydrodynamically interacting active particles. Phys. Rev. Fluids 2 (4), 043104.CrossRefGoogle Scholar
Ramaswamy, S. 2001 Issues in the statistical mechanics of steady sedimentation. Adv. Phys. 50 (3), 297–341.CrossRefGoogle Scholar
Ramaswamy, S. 2010 The mechanics and statistics of active matter. Annu. Rev. Condens. Matter Phys. 1 (1), 323–345.CrossRefGoogle Scholar
Saintillan, D. 2010 The dilute rheology of swimming suspensions: a simple kinetic model. Exp. Mech. 50, 1275–1281.CrossRefGoogle Scholar
Saintillan, D. 2018 Rheology of active fluids. Annu. Rev. Fluid Mech. 50, 563–592.CrossRefGoogle Scholar
Saintillan, D. & Shelley, M. J. 2007 Orientational order and instabilities in suspensions of self-locomoting rods. Phys. Rev. Lett. 99 (5), 058102.CrossRefGoogle ScholarPubMed
Saintillan, D. & Shelley, M. J. 2008 Instabilities and pattern formation in active particle suspensions: kinetic theory and continuum simulations. Phys. Rev. Lett. 100 (17), 178103.CrossRefGoogle ScholarPubMed
Saintillan, D. & Shelley, M. J. 2011 Emergence of coherent structures and large-scale flows in motile suspensions. J. R. Soc. Interface 9 (68), 571–585.CrossRefGoogle ScholarPubMed
Segre, P. N., Herbolzheimer, E. & Chaikin, P. M. 1997 Long-range correlations in sedimentation. Phys. Rev. Lett. 79 (13), 2574.CrossRefGoogle Scholar
Simha, R. A. & Ramaswamy, S. 2002 Hydrodynamic fluctuations and instabilities in ordered suspensions of self-propelled particles. Phys. Rev. Lett. 89 (5), 058101.CrossRefGoogle Scholar
Sokolov, A. & Aranson, I. S. 2009 Reduction of viscosity in suspension of swimming bacteria. Phys. Rev. Lett. 103 (14), 148101.CrossRefGoogle ScholarPubMed
Sokolov, A. & Aranson, I. S. 2012 Physical properties of collective motion in suspensions of bacteria. Phys. Rev. Lett. 109 (24), 248109.CrossRefGoogle ScholarPubMed
Sokolov, A., Goldstein, R. E., Feldchtein, F. I. & Aranson, I. S. 2009 Enhanced mixing and spatial instability in concentrated bacterial suspensions. Phys. Rev. E 80 (3), 031903.CrossRefGoogle ScholarPubMed
Stenhammar, J., Nardini, C., Nash, R. W., Marenduzzo, D. & Morozov, A. 2017 Role of correlations in the collective behavior of microswimmer suspensions. Phys. Rev. Lett. 119 (2), 028005.CrossRefGoogle ScholarPubMed
Subramanian, G. & Brady, J. F. 2006 Trajectory analysis for non-brownian inertial suspensions in simple shear flow. J. Fluid Mech. 559, 151–203.CrossRefGoogle Scholar
Subramanian, G. & Koch, D. L. 2009 Critical bacterial concentration for the onset of collective swimming. J. Fluid Mech. 632, 359–400.CrossRefGoogle Scholar
Subramanian, G. & Nott, P. R. 2011 The fluid dynamics of swimming microorganisms and cells. J. Indian I. Sci. 91, 283–313.Google Scholar
Thiffeault, J.-L. 2015 Distribution of particle displacements due to swimming microorganisms. Phys. Rev. E 92 (2), 023023.CrossRefGoogle ScholarPubMed
Toner, J., Tu, Y. & Ramaswamy, S. 2005 Hydrodynamics and phases of flocks. Ann. Phys. 318 (1), 170–244.CrossRefGoogle Scholar
Toppaladoddi, S. & Balmforth, N. J. 2014 Slender axisymmetric Stokesian swimmers. J. Fluid Mech. 746, 273–299.CrossRefGoogle Scholar
Underhill, P. T. & Graham, M. D. 2011 Correlations and fluctuations of stress and velocity in suspensions of swimming microorganisms. Phys. Fluids 23, 121902.CrossRefGoogle Scholar
Underhill, P. T., Hernandez-Ortiz, J. P. & Graham, M. D. 2008 Diffusion and spatial correlations in suspensions of swimming particles. Phys. Rev. Lett. 100 (24), 248101.CrossRefGoogle ScholarPubMed
Valeriani, C., Li, M., Novosel, J., Arlt, J. & Marenduzzo, D. 2011 Colloids in a bacterial bath: simulations and experiments. Soft Matt. 7 (11), 5228–5238.CrossRefGoogle Scholar
Van Dyke, M. 1964 Perturbation Methods in Fluid Mechanics, vol. 964. Academic Press.Google Scholar
Wensink, H. H., Dunkel, J., Heidenreich, S., Drescher, K., Goldstein, R. E., Löwen, H. & Yeomans, J. M. 2012 Meso-scale turbulence in living fluids. Proc. Natl Acad. Sci. USA 109 (36), 14308–14313.CrossRefGoogle ScholarPubMed
Wioland, H., Lushi, E. & Goldstein, R. E. 2016 Directed collective motion of bacteria under channel confinement. New J. Phys. 18 (7), 075002.CrossRefGoogle Scholar
Woodhouse, F. G. & Goldstein, R. E. 2012 Spontaneous circulation of confined active suspensions. Phys. Rev. Lett. 109 (16), 168105.CrossRefGoogle ScholarPubMed
Wu, K.-T., Hishamunda, J. B., Chen, D. T. N., DeCamp, S. J., Chang, Y.-W., Fernández-Nieves, A., Fraden, S. & Dogic, Z. 2017 Transition from turbulent to coherent flows in confined three-dimensional active fluids. Science 355 (6331), eaal1979.CrossRefGoogle ScholarPubMed
Wu, X. L. & Libchaber, A. 2000 Particle diffusion in a quasi-two-dimensional bacterial bath. Phys. Rev. Lett. 84, 3017–3020.CrossRefGoogle Scholar
Yang, O., Peng, Y., Liu, Z., Tang, C., Xu, X. & Cheng, X. 2016 Dynamics of ellipsoidal tracers in swimming algal suspensions. Phys. Rev. E 94 (4), 042601.CrossRefGoogle ScholarPubMed
Zaid, I. M., Dunkel, J. & Yeomans, J. M. 2011 Lévy fluctuations and mixing in dilute suspensions of algae and bacteria. J. R. Soc. Interface 8 (62), 1314–1331.CrossRefGoogle ScholarPubMed
Zwanzig, R. 2001 Nonequilibrium Statistical Mechanics. Oxford University Press.Google Scholar