Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T08:42:48.236Z Has data issue: false hasContentIssue false
  • English
  • Français

Energetics of horizontal convection

Published online by Cambridge University Press:  28 January 2013

Bishakhdatta Gayen ,
Ross W. Griffiths ,
Graham O. Hughes  and
Juan A. Saenz
Bishakhdatta Gayen
Affiliation:
Research School of Earth Sciences, Australian National University, Canberra, ACT 0200, Australia
Ross W. Griffiths*
Affiliation:
Research School of Earth Sciences, Australian National University, Canberra, ACT 0200, Australia
Graham O. Hughes
Affiliation:
Research School of Earth Sciences, Australian National University, Canberra, ACT 0200, Australia
Juan A. Saenz
Affiliation:
Research School of Earth Sciences, Australian National University, Canberra, ACT 0200, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

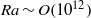Three-dimensional direct numerical simulation of horizontal convection is reported for a large Rayleigh number, $\mathit{Ra}\sim O(1{0}^{12} )$, and boundary conditions that allow comparison with previous laboratory experiments. The convection is forced by heating over half of the horizontal base of a long channel and cooling over the other half of the base. The solutions are consistent with the experiments, including small-scale streamwise roll instability developing into a convectively mixed layer within the bottom thermal boundary layer, and a turbulent endwall plume. The mechanical energy budget is shown to be dominated by conversions of available potential energy to kinetic energy by buoyancy flux in the plume and the reverse in the interior of the circulation. These local conversions are three orders of magnitude greater than the total rate of viscous dissipation. The total irreversible mixing is exactly equal to the generation of available potential energy by buoyancy forcing, and one order of magnitude larger than the viscous dissipation. This confirms that dissipation rate is not an indicator of the strength of the circulation and explains why horizontal convection is more energetic than might be expected.

JFM classification

Convection: Buoyancy-driven instability Convection: Convection Geophysical and Geological Flows: Ocean circulation
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 716 , 10 February 2013 , R10
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Gregory, J. M. & Tailleux, R. 2011 Kinetic energy analysis of the response of the Atlantic meridional overturning circulation to CO2-forced climate change. Clim. Dyn. 37, 893–914.Google Scholar
Hughes, G. O. & Griffiths, R. W. 2008 Horizontal convection. Annu. Rev. Fluid Mech. 40, 185–208.Google Scholar
Hughes, G. O., Griffiths, R. W., Mullarney, J. C. & Peterson, W. H. 2007 A theoretical model for horizontal convection at high Rayleigh number. J. Fluid Mech. 581, 251–276.Google Scholar
Hughes, G. O., Hogg, A. McC. & Griffiths, R. W. 2009 Available potential energy and irreversible mixing in the meridional overturning circulation. J. Phys. Oceanogr. 39, 3130–3146.Google Scholar
Mullarney, J. C., Griffiths, R. W. & Hughes, G. O. 2004 Convection driven by differential heating at a horizontal boundary. J. Fluid Mech. 516, 181–209.CrossRefGoogle Scholar
Paparella, F. & Young, W. R. 2002 Horizontal convection is non-turbulent. J. Fluid Mech. 466, 205–214.Google Scholar
Rossby, H. T. 1965 On thermal convection driven by non-uniform heating from below: an experimental study. Deep Sea Res. 12, 9–16.Google Scholar
Rossby, H. T. 1998 Numerical experiments with a fluid heated non-uniformly from below. Tellus A 50, 242–257.Google Scholar
Saenz, J. A., Hogg, A. McC., Hughes, G. O. & Griffiths, R. W. 2012 Mechanical power input from buoyancy and wind to the circulation in an ocean model. Geophys. Res. Lett. 39, L13605.CrossRefGoogle Scholar
Scotti, A. & White, B. 2011 Is horizontal convection really “non-turbulent”? Geophys. Res. Lett. 38, L21609.Google Scholar
Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2010 Radial boundary layer structure and Nusselt number in Rayleigh–Bénard convection. J. Fluid Mech. 643, 495–507.CrossRefGoogle Scholar
Stewart, K. D., Hughes, G. O. & Griffiths, R. W. 2011 When do marginal seas and topographic sills modify the ocean density structure? J. Geophys. Res. 116, C08021.Google Scholar
Stewart, K. D., Hughes, G. O. & Griffiths, R. W. 2012 The role of turbulent mixing in an overturning circulation maintained by surface buoyancy forcing. J. Phys. Oceanogr. 42, 1907–1922.CrossRefGoogle Scholar
Tailleux, R. 2009 On the energetics of stratified turbulent mixing, irreversible thermodynamics, Boussinesq models and the ocean heat engine controversy. J. Fluid Mech. 638, 339–382.Google Scholar
Turner, J. S. 1986 Turbulent entrainment: the development of the entrainment assumption, and its application in geophysical flows. J. Fluid Mech. 173, 431–471.Google Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.Google Scholar

Gayen et al. supplementary movie

Horizontal velocity field on the spanwise (y) mid-plane for the simulations at Ra = 5.86 x 1011, Pr = 5, and A = 0.16 (grid resolution 513 x 128 x 257 in x, y and z).

Download Gayen et al. supplementary movie(Video)
Video 9.6 MB

Gayen et al. supplementary movie

Vertical velocity field on the spanwise mid-plane for the simulations at Ra = 5.86 x 1011, Pr = 5, and A = 0.16 (grid resolution 513 x 128 x 257 in x, y and z).

Download Gayen et al. supplementary movie(Video)
Video 9.6 MB

Gayen et al. supplementary movie

Temperature field on the spanwise mid-plane for the simulations at Ra = 5.86 x 1011, Pr = 5, and A = 0.16 (grid resolution 513 x 128 x 257 in x, y and z).

Download Gayen et al. supplementary movie(Video)
Video 4.8 MB