Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-19T17:15:50.901Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of Schmidt number on the short-wavelength instabilities in stratified vortices

Published online by Cambridge University Press:  28 March 2019

Suraj Singh  and
Manikandan Mathur Open the ORCID record for Manikandan Mathur [Opens in a new window]
Suraj Singh*
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Madras, Chennai 600036, India
Manikandan Mathur*
Affiliation:
Department of Aerospace Engineering, Indian Institute of Technology Madras, Chennai 600036, India
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a local stability analysis to investigate the effects of differential diffusion between momentum and density (quantified by the Schmidt number 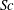$Sc$) on the three-dimensional, short-wavelength instabilities in planar vortices with a uniform stable stratification along the vorticity axis. Assuming small diffusion in both momentum and density, but arbitrary values for 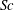$Sc$, we present a detailed analytical/numerical analysis for three different classes of base flows: (i) an axisymmetric vortex, (ii) an elliptical vortex and (iii) the flow in the neighbourhood of a hyperbolic stagnation point. While a centrifugally stable axisymmetric vortex remains stable for any 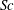$Sc$, it is shown that 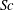$Sc$ can have significant effects in a centrifugally unstable axisymmetric vortex: the range of unstable perturbations increases when 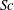$Sc$ is taken away from unity, with the extent of increase being larger for 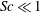$Sc\ll 1$ than for 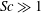$Sc\gg 1$. Additionally, for 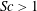$Sc>1$, we report the possibility of oscillatory instability. In an elliptical vortex with a stable stratification, 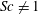$Sc\neq 1$ is shown to non-trivially influence the three different inviscid instabilities (subharmonic, fundamental and superharmonic) that have been previously reported, and also introduce a new branch of oscillatory instability that is not present at 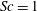$Sc=1$. The unstable parameter space for the subharmonic (instability IA) and fundamental (instability IB) inviscid instabilities are shown to be significantly increased for 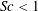$Sc<1$ and 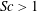$Sc>1$, respectively. Importantly, for sufficiently small and large 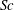$Sc$, respectively, the maximum growth rate for instabilities IA and IB occurs away from the inviscid limit. The new oscillatory instability (instability III) is shown to occur only for sufficiently small 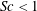$Sc<1$, the signature of which is nevertheless present with zero growth rate in the inviscid limit. The Schmidt number is then shown to play no role in the evolution of transverse perturbations on the flow around a hyperbolic stagnation point with a stable stratification. We conclude by discussing the physical length scales associated with the 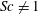$Sc\neq 1$ instabilities, and their potential relevance in various realistic settings.

JFM classification

Geophysical and Geological Flows: Stratified flows Vortex Flows: Vortex instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 867 , 25 May 2019 , pp. 765 - 803
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ajith Kumar, S., Mathur, M., Sameen, A. & Anil Lal, S. 2016 Effects of Prandtl number on the laminar cross flow past a heated cylinder. Phys. Fluids 28 (11), 113603.Google Scholar
Aravind, H. M., Mathur, M. & Dubos, T.2017 Short-wavelength secondary instabilities in homogeneous and stably stratified shear flows. arXiv:1712.05868v2.Google Scholar
Baker, D. J. 1971 Density gradients in a rotating stratified fluid: experimental evidence for a new instability. Science 172 (3987), 1029–1031.Google Scholar
Bayly, B. J. 1986 Three-dimensional instability of elliptical flow. Phys. Rev. Lett. 57 (17), 2160.Google Scholar
Bayly, B. J. 1988 Three-dimensional centrifugal-type instabilities in inviscid two-dimensional flows. Phys. Fluids 31 (1), 56–64.Google Scholar
Billant, P. & Gallaire, F. 2005 Generalized Rayleigh criterion for non-axisymmetric centrifugal instabilities. J. Fluid Mech. 542, 365–379.Google Scholar
Calman, J. 1977 Experiments on high Richardson number instability of a rotating stratified shear flow. Dyn. Atmos. Oceans 1 (4), 277–297.Google Scholar
Carton, X. 2001 Hydrodynamical modeling of oceanic vortices. Surv. Geophys. 22 (3), 179–263.Google Scholar
Corcos, G. M. & Lin, S. J. 1984 The mixing layer: deterministic models of a turbulent flow. Part 2. The origin of the three-dimensional motion. J. Fluid Mech. 139, 67–95.Google Scholar
Cortesi, A. B., Yadigaroglu, G. & Banerjee, S. 1998 Numerical investigation of the formation of three-dimensional structures in stably-stratified mixing layers. Phys. Fluids 10 (6), 1449–1473.Google Scholar
Craik, A. D. D. & Criminale, W. O. 1986 Evolution of wavelike disturbances in shear flows: a class of exact solutions of the Navier–Stokes equations. Proc. R. Soc. Lond. A 406, 13–26.Google Scholar
Davidson, P. A. 2016 Introduction to Magnetohydrodynamics, vol. 55. Cambridge University Press.Google Scholar
Emanuel, K. A. 1991 The theory of hurricanes. Annu. Rev. Fluid Mech. 23 (1), 179–196.Google Scholar
Gallaire, F., Marquillie, M. & Ehrenstein, U. 2007 Three-dimensional transverse instabilities in detached boundary layers. J. Fluid Mech. 571, 221–233.Google Scholar
Godeferd, F. S., Cambon, C. & Leblanc, S. 2001 Zonal approach to centrifugal, elliptic and hyperbolic instabilities in Stuart vortices with external rotation. J. Fluid Mech. 449, 1–37.Google Scholar
Huang, Y. & Yang, V. 2009 Dynamics and stability of lean-premixed swirl-stabilized combustion. Prog. Energy Combust. Sci. 35 (4), 293–364.Google Scholar
Jethani, Y., Kumar, K., Sameen, A. & Mathur, M. 2018 Local origin of mode-b secondary instability in the flow past a circular cylinder. Phys. Rev. Fluids 3 (10), 103902.Google Scholar
Kerswell, R. R. 2002 Elliptical instability. Annu. Rev. Fluid Mech. 34 (1), 83–113.Google Scholar
Kirillov, O. N. & Mutabazi, I. 2017 Short-wavelength local instabilities of a circular Couette flow with radial temperature gradient. J. Fluid Mech. 818, 319–343.Google Scholar
Klaassen, G. P. & Peltier, W. R. 1985 The effect of Prandtl number on the evolution and stability of Kelvin–Helmholtz billows. Geophys. Astrophys. Fluid Dyn. 32 (1), 23–60.Google Scholar
Landman, M. J. & Saffman, P. G. 1987 The three-dimensional instability of strained vortices in a viscous fluid. Phys. Fluids 30 (8), 2339–2342.Google Scholar
Le Dizès, S. 2000 Three-dimensional instability of a multipolar vortex in a rotating flow. Phys. Fluids 12 (11), 2762–2774.Google Scholar
Le Dizes, S. & Eloy, C. 1999 Short-wavelength instability of a vortex in a multipolar strain field. Phys. Fluids 11 (2), 500–502.Google Scholar
Leblanc, S. 1997 Stability of stagnation points in rotating flows. Phys. Fluids 9 (11), 3566–3569.Google Scholar
Lifschitz, A. & Hameiri, E. 1991 Local stability conditions in fluid dynamics. Phys. Fluids 3 (11), 2644–2651.Google Scholar
Mathur, M., Ortiz, S., Dubos, T. & Chomaz, J.-M. 2014 Effects of an axial flow on the centrifugal, elliptic and hyperbolic instabilities in Stuart vortices. J. Fluid Mech. 758, 565–585.Google Scholar
McIntyre, M. E. 1970 Diffusive destabilisation of the baroclinic circular vortex. Geophys. Astrophys. Fluid Dyn. 1 (1–2), 19–57.Google Scholar
Metcalfe, R. W., Orszag, S. A., Brachet, M. E., Menon, S. & Riley, J. J. 1987 Secondary instability of a temporally growing mixing layer. J. Fluid Mech. 184, 207–243.Google Scholar
Meunier, P., Miquel, B. & Le Dizès, S. 2014 Instabilities around a rotating ellipsoid in a stratified rotating flow. In 19th Australasian Fluid Mechanics Conferences, Melbourne, Australia (ed. Chowdhury, H. & Alam, F.), RMIT University.Google Scholar
Miyazaki, T. 1993 Elliptical instability in a stably stratified rotating fluid. Phys. Fluids 5 (11), 2702–2709.Google Scholar
Miyazaki, T. & Fukumoto, Y. 1992 Three-dimensional instability of strained vortices in a stably stratified fluid. Phys. Fluids 4 (11), 2515–2522.Google Scholar
Nagarathinam, D., Sameen, A. & Mathur, M. 2015 Centrifugal instability in non-axisymmetric vortices. J. Fluid Mech. 769, 26–45.Google Scholar
Orszag, S. A. & Patera, A. T. 1983 Secondary instability of wall-bounded shear flows. J. Fluid Mech. 128, 347–385.Google Scholar
Pierrehumbert, R. T. 1986 Universal short-wave instability of two-dimensional eddies in an inviscid fluid. Phys. Rev. Lett. 57 (17), 2157.Google Scholar
Pierrehumbert, R. T. & Widnall, S. E. 1982 The two-and three-dimensional instabilities of a spatially periodic shear layer. J. Fluid Mech. 114, 59–82.Google Scholar
Riedinger, X., Le Dizès, S. & Meunier, P. 2010 Viscous stability properties of a Lamb–Oseen vortex in a stratified fluid. J. Fluid Mech. 645, 255–278.Google Scholar
Sipp, D. & Jacquin, L. 2000 Three-dimensional centrifugal-type instabilities of two-dimensional flows in rotating systems. Phys. Fluids 12 (7), 1740–1748.Google Scholar
Spalart, P. R. 1998 Airplane trailing vortices. Annu. Rev. Fluid Mech. 30 (1), 107–138.Google Scholar
Waite, M. L. & Smolarkiewicz, P. K. 2008 Instability and breakdown of a vertical vortex pair in a strongly stratified fluid. J. Fluid Mech. 606, 239–273.Google Scholar
Yim, E. & Billant, P. 2016 Analogies and differences between the stability of an isolated pancake vortex and a columnar vortex in stratified fluid. J. Fluid Mech. 796, 732–766.Google Scholar