Published online by Cambridge University Press: 16 August 2016
Numerical simulations of three-dimensional rapidly rotating Rayleigh–Bénard convection are performed by employing an asymptotic quasi-geostrophic model that incorporates the effects of no-slip boundaries through (i) parametrized Ekman pumping boundary conditions and (ii) a thermal wind boundary layer that regularizes the enhanced thermal fluctuations induced by pumping. The fidelity of the model, obtained by an asymptotic reduction of the Navier–Stokes equations that implicitly enforces a pointwise geostrophic balance, is explored for the first time by comparisons of simulations against the findings of direct numerical simulations (DNS) and laboratory experiments. Results from these methods have established Ekman pumping as the mechanism responsible for significantly enhancing the vertical heat transport. This asymptotic model demonstrates excellent agreement over a range of thermal forcing for Prandtl number 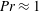 $Pr\approx 1$ when compared with results from experiments and DNS at maximal values of their attainable rotation rates, as measured by the Ekman number (
$Pr\approx 1$ when compared with results from experiments and DNS at maximal values of their attainable rotation rates, as measured by the Ekman number (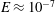 $E\approx 10^{-7}$); good qualitative agreement is achieved for
$E\approx 10^{-7}$); good qualitative agreement is achieved for 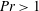 $Pr>1$. Similar to studies with stress-free boundaries, four spatially distinct flow morphologies exists. Despite the presence of frictional drag at the upper and/or lower boundaries, a strong non-local inverse cascade of barotropic (i.e. depth-independent) kinetic energy persists in the final regime of geostrophic turbulence and is dominant at large scales. For mixed no-slip/stress-free and no-slip/no-slip boundaries, Ekman friction is found to attenuate the efficiency of the upscale energy transport and, unlike the case of stress-free boundaries, rapidly saturates the barotropic kinetic energy. For no-slip/no-slip boundaries, Ekman friction is strong enough to prevent the development of a coherent dipole vortex condensate. Instead, vortex pairs are found to be intermittent, varying in both time and strength. For all combinations of boundary conditions, a Nastrom–Gage type of spectrum of kinetic energy is found, where the power-law exponent changes from
$Pr>1$. Similar to studies with stress-free boundaries, four spatially distinct flow morphologies exists. Despite the presence of frictional drag at the upper and/or lower boundaries, a strong non-local inverse cascade of barotropic (i.e. depth-independent) kinetic energy persists in the final regime of geostrophic turbulence and is dominant at large scales. For mixed no-slip/stress-free and no-slip/no-slip boundaries, Ekman friction is found to attenuate the efficiency of the upscale energy transport and, unlike the case of stress-free boundaries, rapidly saturates the barotropic kinetic energy. For no-slip/no-slip boundaries, Ekman friction is strong enough to prevent the development of a coherent dipole vortex condensate. Instead, vortex pairs are found to be intermittent, varying in both time and strength. For all combinations of boundary conditions, a Nastrom–Gage type of spectrum of kinetic energy is found, where the power-law exponent changes from 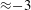 ${\approx}-3$ to
${\approx}-3$ to 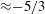 ${\approx}-5/3$, i.e. from steep to shallow, as the spectral wavenumber increases.
${\approx}-5/3$, i.e. from steep to shallow, as the spectral wavenumber increases.