Published online by Cambridge University Press: 02 September 2011
The linear spatiotemporal stability properties of axisymmetric laminar capillary jets with fully developed initial velocity profiles are studied for large values of both the Reynolds number, 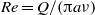 , and the Froude number,
, and the Froude number, 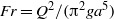 , where
, where  is the injector radius,
is the injector radius, 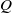 the volume flow rate,
the volume flow rate,  the kinematic viscosity and
the kinematic viscosity and 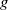 the gravitational acceleration. The downstream development of the basic flow and its stability are addressed with an approximate formulation that takes advantage of the jet slenderness. The base flow is seen to depend on two parameters, namely a Stokes number,
the gravitational acceleration. The downstream development of the basic flow and its stability are addressed with an approximate formulation that takes advantage of the jet slenderness. The base flow is seen to depend on two parameters, namely a Stokes number, 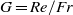 , and a Weber number,
, and a Weber number, 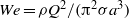 , where
, where 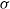 is the surface tension coefficient, while its linear stability depends also on the Reynolds number. When non-parallel terms are retained in the local stability problem, the analysis predicts a critical value of the Weber number,
is the surface tension coefficient, while its linear stability depends also on the Reynolds number. When non-parallel terms are retained in the local stability problem, the analysis predicts a critical value of the Weber number, 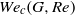 , below which a pocket of local absolute instability exists within the near field of the jet. The function
, below which a pocket of local absolute instability exists within the near field of the jet. The function 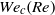 is computed for the buoyancy-free jet, showing marked differences with the results previously obtained with uniform velocity profiles. It is seen that, in accounting for gravity effects, it is more convenient to express the parametric dependence of the critical Weber number with use made of the Morton and Bond numbers,
is computed for the buoyancy-free jet, showing marked differences with the results previously obtained with uniform velocity profiles. It is seen that, in accounting for gravity effects, it is more convenient to express the parametric dependence of the critical Weber number with use made of the Morton and Bond numbers, 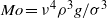 and
and 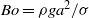 , as replacements for
, as replacements for 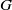 and
and 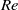 . This alternative formulation is advantageous to describe jets of a given liquid for a known value of
. This alternative formulation is advantageous to describe jets of a given liquid for a known value of 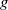 , in that the resulting Morton number becomes constant, thereby leaving
, in that the resulting Morton number becomes constant, thereby leaving 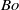 as the only relevant parameter. The computed function
as the only relevant parameter. The computed function 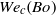 for a water jet under Earth gravity is shown to be consistent with the experimental results of Clanet and Lasheras for the transition from jetting to dripping of water jets discharging into air from long injection needles, which cannot be properly described with a uniform velocity profile assumed at the jet exit.
for a water jet under Earth gravity is shown to be consistent with the experimental results of Clanet and Lasheras for the transition from jetting to dripping of water jets discharging into air from long injection needles, which cannot be properly described with a uniform velocity profile assumed at the jet exit.