Article contents
The effect of an unsteady flow incident on an array of circular cylinders
Published online by Cambridge University Press: 13 June 2019
Abstract
In this paper we investigate the effect of an inhomogeneous and unsteady velocity field incident on an array of rigid circular cylinders arranged within a circular perimeter (diameter 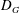 $D_{G}$) of varying solid fraction
$D_{G}$) of varying solid fraction 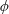 $\unicode[STIX]{x1D719}$, where the unsteady flow is generated by placing a cylinder (diameter
$\unicode[STIX]{x1D719}$, where the unsteady flow is generated by placing a cylinder (diameter 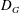 $D_{G}$) upwind of the array. Unsteady two-dimensional viscous simulations at a moderate Reynolds number (
$D_{G}$) upwind of the array. Unsteady two-dimensional viscous simulations at a moderate Reynolds number (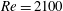 $Re=2100$) and also, as a means of extrapolating to a flow with a very high Reynolds number, inviscid rapid distortion theory (RDT) calculations were carried out. These novel RDT calculations required the circulation around each cylinder to be zero which was enforced using an iterative method. The two main differences which were highlighted was that the RDT calculations indicated that the tangential velocity component is amplified, both, at the front and sides of the array. For the unsteady viscous simulations this result did not occur as the two-dimensional vortices (of similar size to the array) are deflected away from the boundary and do not penetrate into the boundary layer. Secondly, the amplification is greater for the RDT calculations as for the unsteady finite Reynolds number calculations. For the two highest solid fraction arrays, the mean flow field has two recirculation regions in the near wake of the array, with closed streamlines that penetrate into the array which will have important implications for scalar transport. The increased bleed through the array at the lower solid fraction results in this recirculation region being displaced further downstream. The effect of inviscid blocking and viscous drag on the upstream streamwise velocity and strain field is investigated as it directly influences the ability of the large coherent structures to penetrate into the array and the subsequent forces exerted on the cylinders in the array. The average total force on the array was found to increase monotonically with increasing solid fraction. For high solid fraction
$Re=2100$) and also, as a means of extrapolating to a flow with a very high Reynolds number, inviscid rapid distortion theory (RDT) calculations were carried out. These novel RDT calculations required the circulation around each cylinder to be zero which was enforced using an iterative method. The two main differences which were highlighted was that the RDT calculations indicated that the tangential velocity component is amplified, both, at the front and sides of the array. For the unsteady viscous simulations this result did not occur as the two-dimensional vortices (of similar size to the array) are deflected away from the boundary and do not penetrate into the boundary layer. Secondly, the amplification is greater for the RDT calculations as for the unsteady finite Reynolds number calculations. For the two highest solid fraction arrays, the mean flow field has two recirculation regions in the near wake of the array, with closed streamlines that penetrate into the array which will have important implications for scalar transport. The increased bleed through the array at the lower solid fraction results in this recirculation region being displaced further downstream. The effect of inviscid blocking and viscous drag on the upstream streamwise velocity and strain field is investigated as it directly influences the ability of the large coherent structures to penetrate into the array and the subsequent forces exerted on the cylinders in the array. The average total force on the array was found to increase monotonically with increasing solid fraction. For high solid fraction 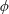 $\unicode[STIX]{x1D719}$, although the fluctuating forces on the individual cylinders is lower than for low
$\unicode[STIX]{x1D719}$, although the fluctuating forces on the individual cylinders is lower than for low 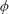 $\unicode[STIX]{x1D719}$, these forces are more correlated due to the proximity of the cylinders. The result is that for mid to high solid fraction arrays the fluctuating force on the array is insensitive to
$\unicode[STIX]{x1D719}$, these forces are more correlated due to the proximity of the cylinders. The result is that for mid to high solid fraction arrays the fluctuating force on the array is insensitive to 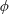 $\unicode[STIX]{x1D719}$. For low
$\unicode[STIX]{x1D719}$. For low 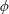 $\unicode[STIX]{x1D719}$, where the interaction of the cylinders is weak, the force statistics on the individual cylinders can be accurately estimated from the local slip velocity that occurs if the cylinders were removed.
$\unicode[STIX]{x1D719}$, where the interaction of the cylinders is weak, the force statistics on the individual cylinders can be accurately estimated from the local slip velocity that occurs if the cylinders were removed.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 12
- Cited by


