Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-04T19:27:59.005Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of line plumes on horizontal surfaces in turbulent convection

Published online by Cambridge University Press:  14 May 2014

G. S. Gunasegarane  and
Baburaj A. Puthenveettil
G. S. Gunasegarane
Affiliation:
Department of Applied Mechanics, Indian Institute of Technology Madras, Chennai, 600036, India
Baburaj A. Puthenveettil*
Affiliation:
Department of Applied Mechanics, Indian Institute of Technology Madras, Chennai, 600036, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the dynamics of line plumes on the bottom horizontal plate in turbulent convection over six decades of Rayleigh number 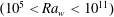$(10^5<\mathit{Ra}_w<10^{11})$ and two decades of Prandtl number or Schmidt number (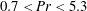$0.7<\mathit{Pr}<5.3$, 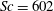$\mathit{Sc}=602$). From the visualisations of these plumes in a horizontal plane close to the plate, we identify the main dynamics as (i) motion along the plumes, (ii) lateral merging of the plumes and (iii) initiation of the plumes; various other minor types of motion also occur along with these main dynamics. In quantifying the three main motions, we first find that the spatiotemporal mean velocity along the length of the plumes (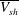$\overline{V_{sh}}$) scales as the large-scale flow velocity (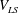$V_{LS}$), with the fraction of the length of the plumes affected by shear increasing with 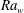$\mathit{Ra}_w$ as 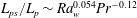$L_{ps}/L_p\sim \mathit{Ra}_w^{0.054} \mathit{Pr}^{-0.12}$. The mean time of initiation of the plumes 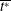$\overline{t^{*}}$, scales as the diffusive time scale near the plate, 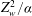$Z_w^2/\alpha $, where 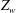$Z_w$ is the appropriate length scale near the plate, in agreement with Howard (Proc. 11th Int. Congress Applied Mechanics, Munich, 1964, pp. 1109–1115). Merging occurs in a large fraction of the area of the plate, with 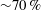${\sim }70\, \%$ of the length of the plumes undergoing merging at 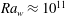$\mathit{Ra}_w\approx 10^{11}$ and 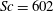$\mathit{Sc}= 602$. The fraction of the length of the plumes that undergoes merging decreases with increase in 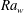$\mathit{Ra}_w$ as, 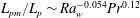$L_{pm}/L_p \sim \mathit{Ra}_w^{-0.054} \mathit{Pr}^{0.12}$; the exponents of 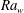$\mathit{Ra}_w$ and 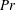$\mathit{Pr}$ being of the same magnitude but of opposite sign as that in the relation for 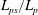$L_{ps}/L_p$. Measurements of the locational means of the velocities of merging of the plumes 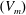$(V_m)$ show that 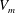$V_m$ is a constant during each merging cycle at any location. However, the values of these constant velocities depend on the location and the time of measurement, since the merging velocities are affected by the local shear, which is a function of space and time at any 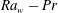$\mathit{Ra}_w-\mathit{Pr}$ combination. The merging velocities at all 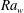$\mathit{Ra}_w$ and 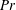$\mathit{Pr}$ have a common lognormal distribution, but their mean and variance increased with increasing 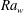$\mathit{Ra}_w$ and decreasing 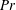$\mathit{Pr}$. Using mass and momentum balance of the region between two merging plumes, we show that the spatiotemporal mean merging velocities (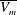$\overline{V_m}$), which are an order lower than 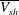$\overline{V_{sh}}$, scale as the entrainment velocity at the sides of the plumes, averaged over the height of the diffusive layer near the plate. This implies that 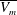$\overline{V_m}$ scales as the diffusive velocity scale near the plate 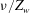$\nu /Z_w$. The Reynolds number in terms of 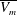$\overline{V_m}$ and the layer height 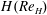$H(\mathit{Re}_H)$ scales as 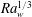$\mathit{Ra}_w^{1/3}$, in the same way as the Nusselt number (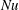$\mathit{Nu}$) scales approximately; therefore 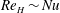$\mathit{Re}_{H}\sim \mathit{Nu}$. These relations imply that 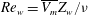$\mathit{Re}_w= \overline{V_m}Z_w/\nu $ a Reynolds number near the plate, is an invariant for a given fluid in turbulent convection.

JFM classification

Convection: Convection Convection: Plumes/thermals Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 749 , 25 June 2014 , pp. 37 - 78
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Bodenschatz, E., Funfschilling, D., Grossmann, S., He, X., Lohse, D., Stevens, R. J. A. M. & Verzicco, R. 2012 Logarithmic temperature profiles in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 109, 114501.Google Scholar
Ahlers, G., Grossman, S. & Lohse, D. 2009 Heat transfer and large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Baker, J. D. 1966 A technique for the precise measurement of small flow velocities. J. Fluid Mech. 26 (3), 573–575.Google Scholar
Bosbach, J., Weiss, S. & Ahlers, G. 2012 Plume fragmentation by bulk interactions in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 054501.Google Scholar
Deardorff, J. 1970 Convective velocity and temperature scales for the unstable planetary boundary layer and for Rayleigh convection. J. Atmos. Sci. 27, 1211–1213.Google Scholar
Funfschilling, D. & Ahlers, G. 2004 Plume motion and large scale circulation in a cylindrical Rayleigh–Bénard cell. Phys. Rev. Lett. 92 (19), 194502.CrossRefGoogle Scholar
Gebhart, B., Pera, L. & Schorr, A. W. 1970 Steady laminar natural convection plume above a horizontal line heat source. Intl J. Heat Mass Transfer 13, 161–171.Google Scholar
Grossman, S. & Lohse, D. 2002 Prandtl and Rayleigh number dependence of the Reynolds number in turbulent convection. Phys. Rev. E 66, 016305.Google Scholar
Gunasegarane, G. S.2014 Structure and dynamics of plumes in turbulent convection. PhD thesis, Department of Applied Mechanics, IIT Madras.Google Scholar
Haramina, T. & Tilgner, A. 2004 Coherent structures in boundary layers of Rayleigh–Bénard convection. Phys. Rev. E 69, 056306.Google Scholar
Hogg, J. & Ahlers, G. 2013 Reynolds number measurements for low-Prandtl-number turbulent convection of large aspect-ratio samples. J. Fluid Mech. 725, 664–680.Google Scholar
Howard, L. N.1964 Convection at high Rayleigh number. In Proc. 11th Int. Congress Applied Mechanics, Munich (ed. H. Gortler), pp. 1109–1115.Google Scholar
Husar, R. B. & Sparrow, E. M. 1968 Patterns of free convection flow adjacent to horizontal heated surfaces. Intl J. Heat Mass Transfer 11, 1208–1211.Google Scholar
Lam, S., Shang, X., Zhou, S. & Xia, K. 2002 Prandtl number dependence of the viscous boundary layer and the Reynolds numbers in Rayleigh number convection. Phys. Rev. E 65, 066306.Google Scholar
Parodi, A., Hardenberg, J., Passoni, G., Provenzale, A. & Spiegel, E. 2004 Clustering of plumes in turbulent convection. Phys. Rev. Lett. 92 (19), 194503.Google Scholar
Pera, L. & Gebhart, B. 1973 On the stability of natural convection boundary layer flow over horizontal and slightly inclined surfaces. Intl J. Heat Mass Transfer 16, 1147–1163.CrossRefGoogle Scholar
Puthenveettil, B. A., Ananthakrishna, G. & Arakeri, J. H. 2005 Multifractal nature of plume structure in high Rayliegh number convection. J. Fluid Mech. 526, 245–256.CrossRefGoogle Scholar
Puthenveettil, B. A. & Arakeri, J. H. 2005 Plume structure in high Rayleigh number convection. J. Fluid Mech. 542, 217–249.Google Scholar
Puthenveettil, B. A. & Arakeri, J. H. 2008 Convection due to an unstable density difference across a permeable membrane. J. Fluid Mech. 609, 139–170.Google Scholar
Puthenveettil, B. A., Gunasegarane, G. S., Yogesh, K. A., Schmeling, D., Bosbach, J. & Arakeri, J. H. 2011 Length of near-wall plumes in turbulent convection. J. Fluid Mech. 685, 335–364.Google Scholar
Qiu, X. L. & Xia, K. Q. 1998 Spatial structure of the viscous boundary layer in turbulent convection. Phys. Rev. E 58, 5816–5820.Google Scholar
Ramareddy, G. V. & Puthenveettil, B. A. 2011 The $\mathit{Pe}\sim 1$ regime of convection across a horizontal permeable membrane. J. Fluid Mech. 679, 476–504.Google Scholar
Schneider, W. 1981 Flow induced by jets and plumes. J. Fluid Mech. 108, 55–65.Google Scholar
Shi, N., Emran, M. S. & Schumacher, J. 2012 Boundary layer structure in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 706, 5–33.Google Scholar
Shishkina, O. & Thess, A. 2009 Mean temperature profiles in turbulent Rayleigh–Bénard convection of water. J. Fluid Mech. 633, 449–460.Google Scholar
Shishkina, O. & Wagner, C. 2008 Analysis of sheet-like thermal plumes in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 599, 383–404.Google Scholar
Spangenberg, W. G. & Rowland, W. G. 1961 Convective circulation in water induced by evaporative cooling. Phys. Fluids 4 (6), 743–750.CrossRefGoogle Scholar
Theerthan, S. A. & Arakeri, J. H. 1998 A model for near-wall dynamics in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 373, 221–254.CrossRefGoogle Scholar
Theerthan, S. A. & Arakeri, J. H. 2000 Planform structure and heat transfer in turbulent free convection over horizontal surfaces. Phys. Fluids 12, 884–894.Google Scholar
Vorobieff, P. & Ecke, R. 2002 Turbulent rotating convection: an experimental study. J. Fluid Mech. 458, 191–218.Google Scholar
Xia, K. Q., Lam, S. & Zhou, S. Q. 2002 Heat flux measurement in high Prandtl number turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 88 (6), 064501.Google Scholar
Zhou, Q., Sun, C. & Xia, K. Q. 2007 Morphological evolution of thermal plumes in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98, 074501.Google Scholar
Zhou, Q. & Xia, K. Q. 2010 Physical and geometrical properties of thermal plumes in turbulent Rayleigh–Bénard convection. New J. Phys. 12, 075006.Google Scholar
Zocchi, G., Moses, E. & Libchaber, A. 1990 Coherent structures in turbulent convection, an experimental study. Physica A 166, 387–407.Google Scholar