Published online by Cambridge University Press: 22 November 2018
An explosive gas mixture of hydrogen and oxygen is introduced in liquid water between two horizontal walls, forming a flat cylindrical bubble. Ignition and explosion of the bubble lead to a large depressurized cavity that finally implodes. We investigate the dynamics of the bubble collapse, which is qualitatively similar to the collapse of a spherical bubble. It exhibits a slightly weaker singularity than for spherical bubbles. We also analyse the explosion process. Starting with an initial radius 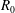 $R_{0}$, the bubble reaches a maximal radius
$R_{0}$, the bubble reaches a maximal radius 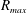 $R_{max}$ that depends on the gap thickness
$R_{max}$ that depends on the gap thickness 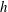 $h$ between the two walls: for a thinner gap, the condensation of water vapour is more efficient, the overpressure consecutive to the combustion is weaker, and its duration is shorter. This leads to a smaller maximal radius
$h$ between the two walls: for a thinner gap, the condensation of water vapour is more efficient, the overpressure consecutive to the combustion is weaker, and its duration is shorter. This leads to a smaller maximal radius 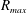 $R_{max}$. An indirect measurement of the transport coefficient of hot water vapour can be inferred from this observation.
$R_{max}$. An indirect measurement of the transport coefficient of hot water vapour can be inferred from this observation.
Expansion of a pure stoichiometric bubble with gap height h=0.92 mm, and initial radius $R_0$ = 2.1 mm. At maximal expansion, $R_{max}=3.1 mm$
Expansion of a bubble containing 50\% of inert gas, with similar characteristics of the bubble shown in movie 3: same gap height h=0.92 mm, and nearly same initial radius $R_0$ = 2 mm. Although this bubble contains less chemical energy it reaches a much larger maximal expansion ($R_{max}=3.9 mm ). As the inert gas do not condense they contribute significantly to the bubble expansion.