Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-21T14:43:16.988Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of a deformable, transversely rotating droplet released into a uniform flow

Published online by Cambridge University Press:  30 August 2011

Eric K. W. Poon ,
Shaoping Quan ,
Jing Lou ,
Matteo Giacobello  and
Andrew S. H. Ooi
Eric K. W. Poon
Affiliation:
Institute of High Performance Computing, 1 Fusionopolis Way, No. 16-16 Connexis, Singapore 138632, Singapore Department of Mechanical Engineering, University of Melbourne, Parkville, Victoria 3010, Australia
Shaoping Quan*
Affiliation:
Institute of High Performance Computing, 1 Fusionopolis Way, No. 16-16 Connexis, Singapore 138632, Singapore
Jing Lou
Affiliation:
Institute of High Performance Computing, 1 Fusionopolis Way, No. 16-16 Connexis, Singapore 138632, Singapore
Matteo Giacobello
Affiliation:
Air Vehicles Division, Defence Science and Technology Organisation, 506 Lorimer Street, Fishermans Bend, Victoria 3207, Australia
Andrew S. H. Ooi
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Parkville, Victoria 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The effects of transverse rotation on the dynamics of a droplet released into a uniform free stream are numerically investigated. The range of the dimensionless rotation rate is limited to 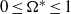, to avoid any possibility of the droplet breaking up. Droplet dynamics and deformations undergo distinct changes when the dimensionless rotational rate 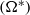reaches a critical value. The critical rotational rate 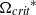is sensitive to the change in the density ratio, but less dependent on the viscosity ratio and interfacial tension. Below 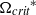, the droplet drag coefficients are reduced marginally as the effect of the rotation is quickly suppressed by the free stream. Above 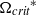, the drag coefficients decrease initially as the rotation effect dominates at earlier times, resulting in a global minimum. The drag coefficients increase monotonically at later times, when the rotation effects decrease and the free-stream effects become dominant. The only exception is with the increase in the viscosity ratio and the surface tension, which either inhibits droplet deformation or restores the droplet to a more spherical shape in the late stages of droplet evolution. The droplet also experiences lift due to the effects of the transverse rotation. It is observed that the lift coefficients are less dependent on the droplet frontal area as the lift is generated by the velocity difference between the upper and lower interface. In general, the lift coefficients increase with 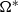at earlier times and decrease at later times as the difference in the velocity between the upper and lower interface decreases. In some extreme cases, the lift coefficients even become negative.

JFM classification

Drops and Bubbles: Drops and Bubbles
Type
Papers
Information
Journal of Fluid Mechanics , Volume 684 , 10 October 2011 , pp. 227 - 250
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Annamalai, P., Trinh, E. & Wang, T. G. 1985 Experimental study of the oscillations of a rotating drop. J. Fluid Mech. 158, 317–327.CrossRefGoogle Scholar
2. Biswas, A., Leung, E. W. & Trinh, E. H. 1991 Rotation of ultrasonically levitated glycerol drops. J. Acoust. Soc. Am. 90, 1502–1507.CrossRefGoogle Scholar
3. Bohr, N. & Wheeler, J. A. 1939 The mechanism of nuclear fission. Phys. Rev. 56 (5), 426–450.CrossRefGoogle Scholar
4. Brown, R. A. & Scriven, L. E. 1980 The shape and stability of rotating liquid drops. Proc. R. Soc. Lond. A 371, 331–357.Google Scholar
5. Busse, F. H. 1984 Oscillations of a rotating liquid drop. J. Fluid Mech. 142, 1–8.CrossRefGoogle Scholar
6. Cardoso, V. & Gualtieri, L. 2006 Equilibrium configurations of fluids and their stability in higher dimensions. Class. Quant. Grav. 23 (24), 7151–7198.CrossRefGoogle Scholar
7. Chabert, M., Dorfman, K. D. & Viovy, J. L. 2005 Droplet fusion by alternating current (AC) field electrocoalescence in microchannels. Electrophoresis 26, 3706–3715.CrossRefGoogle ScholarPubMed
8. Chabreyrie, R., Vainchtein, D., Chandre, C., Singh, P. & Aubry, N. 2010 Using resonances for the control of chaotic mixing within a translating and rotating droplet. Commun. Nonlinear Sci. Numer. Simul. 15, 2124–2132.CrossRefGoogle Scholar
9. Chandrasekhar, S. 1965 The stability of a rotating liquid drop. Proc. R. Soc. Lond. A 286, 1–26.Google Scholar
10. Chang, W., Giraldo, F. & Perot, B. 2002 Analysis of an exact fractional step method. J. Comput. Phys. 180, 183–199.CrossRefGoogle Scholar
11. Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. Phys. Fluids A 2, 765–777.CrossRefGoogle Scholar
12. Dai, M. & Schmidt, D. P. 2005 Adaptive tetrahedral meshing in free-surface flow. J. Comput. Phys. 208, 228–252.CrossRefGoogle Scholar
13. Dai, M., Wang, H., Perot, B. J. & Schmidt, D. P. 2002 Direct interface tracking of droplet deformation. Atomiz. Sprays 12, 721–735.Google Scholar
14. DeBar, R. 1974 Fundamentals of the KRAKEN code. Tech Rep. UCIR-760. Lawrence Livermore National Laboratory.Google Scholar
15. Feng, J., Hu, H. H. & Joseph, D. D. 1994 Direct simulation of initial value problems for the motion of solid bodies in a Newtonian fluid. Part 1. Sedimentation. J. Fluid Mech. 261, 95–134.CrossRefGoogle Scholar
16. Haeberle, S., Naegele, L., Zengerle, R. & Durcée, J. 2006 A digital centrifugal droplet-switch for routing of liquids. In 10th International Conference on Miniaturized Systems for Chemistry and Life Sciences, Tokyo, Japan (ed. Kitamori, T., Fujita, H. & Hasebe, S. ). pp. 570–572. Society for Chemistry and Micro-Nano Systems.Google Scholar
17. He, M., Edgar, J. S., Jeffries, G. D. M., Lorenz, R. M., Shelby, J. P. & Chiu, D. T. 2005 Selective encapsulation of single cells and subcellular organelles into picoliter- and femtoliter-volume droplets. Anal. Chem. 77, 1539–1544.CrossRefGoogle ScholarPubMed
18. Hsiang, L. P. & Faeth, G. M. 1992 Near-limit drop deformation and secondary breakup. Intl J. Multiphase Flow 18, 635–652.CrossRefGoogle Scholar
19. Khan, M. S., Kannangara, D., Shen, W. & Garnier, G. 2008 Isothermal noncoalescence of liquid droplets at the air–liquid interface. Langmuir 24, 3199–3204.CrossRefGoogle ScholarPubMed
20. Knupp, P. M. 2003 Algebraic mesh quality metrics for unstructured initial meshes. Finite Elem. Anal. Des. 39, 217–241.CrossRefGoogle Scholar
21. Lamb, H. 1945 Hydrodynamics, 6th edn. Dover.Google Scholar
22. Lee, C. P., Anilkumart, A. V., Hmelo, A. B. & Wang, T. G. 1998 Equilibrium of liquid drops under the effects of rotation and acoustic flattening: results from USML-2 experiments in space. J. Fluid Mech. 357, 43–67.CrossRefGoogle Scholar
23. Lee, C. P., Lyell, M. J. & Wang, T. G. 1985 Viscous damping of the oscillations of a rotating simple drop. Phys. Fluids 28 (11), 3187–3188.CrossRefGoogle Scholar
24. Li, Z. L. & Lai, M. C. 2001 The immersed interface method for the Navier–Stokes equations with singular forces. J. Comput. Phys. 171, 822–842.CrossRefGoogle Scholar
25. Loth, E. & Dorgan, A. J. 2009 An equation of motion for particles of finite Reynolds number and size. Environ. Fluid Mech. 9, 187–206.CrossRefGoogle Scholar
26. Lubarsky, E., Reichel, J. R., Zinn, B. T. & McAmis, R. 2010 Spray in crossflow: dependence on Weber number. Trans. ASME: J. Engng Gas Turbines Power 132, 021501.Google Scholar
27. Osher, S. & Fedkiw, R. P. 2001 Level set methods: an overview and some recent results. J. Comput. Phys. 169, 463–502.CrossRefGoogle Scholar
28. Pearlman, H. G. & Sohrab, S. H. 1991 The role of droplet rotation in turbulent spray combustion modeling. Combust. Sci. Technol. 76, 321–334.CrossRefGoogle Scholar
29. Perot, B. & Nallapati, R. 2003 A moving unstructured staggered mesh method for the simulation of incompressible free-surface flows. J. Comput. Phys. 184, 192–214.CrossRefGoogle Scholar
30. Plateau, J. A. F. 1863 Experimental and theoretical researches on the figures of equilibrium of a liquid mass withdrawn from the action of gravity. In Annual Report of the Board of Regents of the Smithsonian Institution, Washington, DC, pp. 270–285.Google Scholar
31. Quan, S. P. 2011 Simulations of multiphase flows with multiple length scales using moving mesh interface tracking with adaptive meshing. J. Comput. Phys. 230, 5430–5448.CrossRefGoogle Scholar
32. Quan, S. P., Lou, J. & Schmidt, D. P. 2009a Modeling merging and breakup in the moving mesh interface tracking method for multiphase flow simulations. J. Comput. Phys. 228, 2660–2675.CrossRefGoogle Scholar
33. Quan, S. P. & Schmidt, D. P. 2006 Direct numerical study of a liquid droplet impulsively accelerated by gaseous flow. Phys. Fluids 18, 102103.CrossRefGoogle Scholar
34. Quan, S. P. & Schmidt, D. P. 2007 A moving mesh interface tracking method for 3D incompressible two-phase flows. J. Comput. Phys. 221, 761–780.CrossRefGoogle Scholar
35. Quan, S. P., Schmidt, D. P., Hua, J. & Lou, J. 2009b A numerical study of the relaxation and breakup of an elongated drop in a viscous liquid. J. Fluid Mech. 640, 235–264.CrossRefGoogle Scholar
36. Rhim, W. K., Chung, S. K. & Elleman, D. D. 1988 Experiments on rotating charged liquid drops. In Drops and Bubbles: 3rd Intl Colloq. AIP Conf. Proc. Monterey, CA (ed. T. G. Wang).Google Scholar
37. Sethian, J. A. & Smereka, P. 2003 Level set methods for fluid interfaces. Annu. Rev. Fluid Mech. 35, 341–372.CrossRefGoogle Scholar
38. Son, Y., Kim, C., Yang, D. H. & Ahn, D. J. 2008 Spreading of an inkjet droplet on a solid surface with a controlled contact angle at low Weber and Reynolds numbers. Langmuir 24, 2900–2907.CrossRefGoogle ScholarPubMed
39. Swaminathan, T. N., Mukundakrishnan, K. & Hu, H. H. 2006 Sedimentation of an ellipsoid inside an infinitely long tube at low and intermediate Reynolds numbers. J. Fluid Mech. 551, 357–385.CrossRefGoogle Scholar
40. Tan, Z. W., Teo, S. G. G. & Hu, J. 2008 Ultrasonic generation and rotation of a small droplet at the tip of a hypodermic needle. J. Appl. Phys. 146, 501–523.Google Scholar
41. Temkin, S. & Kim, S. S. 1980 Droplet motion induced by weak shock waves. J. Fluid Mech. 96, 133–157.CrossRefGoogle Scholar
42. Unverdi, S. O. & Tryggvason, G. 1992 A front-tracking method for viscous, incompressible, multi-fluid flows. J. Comput. Phys. 100, 25–37.CrossRefGoogle Scholar
43. Wang, T. G., Anilkumart, A. V., Lee, C. P. & Lin, K. C. 1994 Bifurcation of rotating liquid drops: results from USML-1 experiments in space. J. Fluid Mech. 276, 389–403.CrossRefGoogle Scholar
44. Wang, T. G., Trinh, E. H., Croonquist, A. P. & Elleman, D. D. 1986 The shape of rotating free drops: Spacelab experimental results. Phys. Rev. Lett. 56, 452–455.CrossRefGoogle ScholarPubMed
45. Watanabe, T. 2008 Numerical simulation of oscillations and rotations of a free liquid droplet using the level set method. Comput. Fluids 31, 91–98.CrossRefGoogle Scholar
46. Youngren, G. K. & Acrivos, A. 1976 On the shape of a gas bubble in a viscous extensional flow. J. Fluid Mech. 76, 433–442.CrossRefGoogle Scholar
47. Youngs, D. L. 1982 Time-dependent multimaterial flow with large fluid distortion. In Numerical Methods for Fluid Dynamics (ed. Morton, K. W. & Baines, M. J. ), pp. 273–285. Academic.Google Scholar
48. Zhang, X., Schmidt, D. & Perot, B. 2002 Accuracy and conservation properties of a three-dimensional unstructured staggered mesh scheme for fluid dynamics. J. Comput. Phys. 175, 764–791.CrossRefGoogle Scholar
49. Zheng, H. W., Shu, C. & Chew, Y. T. 2006 A lattice Boltzmann model for multiphase flows with large density ratio. J. Comput. Phys. 218 (1), 353–371.CrossRefGoogle Scholar