Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-18T20:52:38.172Z Has data issue: false hasContentIssue false
  • English
  • Français

Dispersion in the large-deviation regime. Part 2. Cellular flow at large Péclet number

Published online by Cambridge University Press:  19 March 2014

P. H. Haynes  and
J. Vanneste
P. H. Haynes
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
J. Vanneste*
Affiliation:
School of Mathematics and Maxwell Institute for Mathematical Sciences, University of Edinburgh, King’s Buildings, Edinburgh EH9 3JZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A standard model for the study of scalar dispersion through the combined effect of advection and molecular diffusion is a two-dimensional periodic flow with closed streamlines inside periodic cells. Over long time scales, the dispersion of a scalar released in this flow can be characterized by an effective diffusivity that is a factor 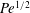$\mathit{Pe}^{1/2}$ larger than molecular diffusivity when the Péclet number 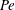$\mathit{Pe}$ is large. Here we provide a more complete description of dispersion in this regime by applying the large-deviation theory developed in Part 1 of this paper. Specifically, we derive approximations to the rate function governing the scalar concentration at large time $t$ by carrying out an asymptotic analysis of the relevant family of eigenvalue problems. We identify two asymptotic regimes and, for each, make predictions for the rate function and spatial structure of the scalar. Regime I applies to distances 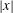$|\boldsymbol {x}|$ from the scalar release point that satisfy 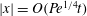$|\boldsymbol {x}|= O(\mathit{Pe}^{1/4} t)$. The concentration in this regime is isotropic at large scales, is uniform along streamlines within each cell, and varies rapidly in boundary layers surrounding the separatrices between adjacent cells. The results of homogenization theory, yielding the 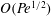$O(\mathit{Pe}^{1/2})$ effective diffusivity, are recovered from our analysis in the limit 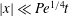$|\boldsymbol {x}|\ll \mathit{Pe}^{1/4} t$. Regime II applies when 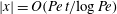$|\boldsymbol {x}|=O(\mathit{Pe}\, t/{\rm log}\, \mathit{Pe})$ and is characterized by an anisotropic concentration distribution that is localized around the separatrices. A novel feature of this regime is the crucial role played by the dynamics near the hyperbolic stagnation points. A consequence is that in part of the regime the dispersion can be interpreted as resulting from a random walk on the lattice of stagnation points. The two regimes overlap so that our asymptotic results describe the scalar concentration over a large range of distances 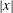$|\boldsymbol {x}|$. They are verified against numerical solutions of the family of eigenvalue problems yielding the rate function.

JFM classification

Mixing: Chaotic advection Reacting Flows: Laminar reacting flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 745 , 25 April 2014 , pp. 351 - 377
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abel, M., Cencini, M., Vergni, D. & Vulpiani, A. 2002 Front speed enhancement in cellular flows. Chaos 12, 481–488.Google Scholar
Bensoussan, A., Lions, J. L. & Papanicolaou, G. C. 1989 Asymptotic Analysis of Periodic Structures. Kluwer.Google Scholar
Childress, S. 1979 Alpha-effect in flux ropes and sheets. Phys. Earth Planet. Inter. 20, 172–180.Google Scholar
Childress, S. & Soward, A. M. 1989 Scalar transport and alpha-effect for a family of cat’s-eye flows. J. Fluid Mech. 205, 99–133.Google Scholar
Dembo, A. & Zeitouni, O. 1998 Large Deviations: Techniques and Applications. Springer.CrossRefGoogle Scholar
den Hollander, F. 2000 In Large Deviations Fields Institute Monographs, American Mathematical Society.Google Scholar
DLMF 2010, Digital library of mathematical functions, from http://dlmf.nist.gov/.Google Scholar
Ellis, R. S. 1995 An overview of the theory of large deviations and applications to statistical physics. Actuar. J. 1, 97–142.Google Scholar
Fannjiang, A. & Papanicolaou, G. 1994 Enhanced diffusion for periodic flows. SIAM J. Appl. Maths 54, 333–408.Google Scholar
Freidlin, M. 1985 Functional Integration and Partial Differential Equations. Princeton University Press.Google Scholar
Freidlin, M. & Wentzell, A. 1994 Random Perturbations of Hamiltonian Systems. American Mathematical Society.CrossRefGoogle Scholar
Gärtner, J. & Freidlin, M. I. 1979 The propagation of concentration waves in periodic and random media. Sov. Math. Dokl. 20, 1282–1286.Google Scholar
Gorb, Y., Nam, D. & Novikov, A. 2011 Numerical simulations of diffusion in cellular flows at high Péclet number. Discrete Continuous Dyn. Syst. B 15, 75–92.Google Scholar
Haynes, P. H. & Vanneste, J. 2005 What controls the decay rate of passive scalars in smooth random flows?. Phys. Fluids 17, 097103.Google Scholar
Haynes, P. H. & Vanneste, J. 2014 Dispersion in the large-deviation regime. Part 1. Shear flows and periodic flows. J. Fluid Mech. 745, 321–350.Google Scholar
Keller, J. B. 2004 Diffusion at finite speed and random walks. Proc. Natl Acad. Sci. USA 101, 1120–1122.Google Scholar
Koralov, L. 2004 Random perturbations of two-dimensional Hamiltonian flows. Probab. Theory Related Fields 129, 37–62.Google Scholar
Majda, A. J. & Kramer, P. R. 1999 Simplified models for turbulent diffusion: theory, numerical modelling and physical phenomena. Phys. Rep. 314, 237–574.CrossRefGoogle Scholar
Moffatt, H. K. 1983 Transport effects associated with turbulence with particular attention to the influence of helicity. Rep. Prog. Phys. 46, 621–664.Google Scholar
Novikov, A., Papanicolaou, G. & Ryzhik, L. 2005 Boundary layers for cellular flows at high Péclet numbers. Commun. Pure Appl. Maths 867–922, 563–580.Google Scholar
Novikov, A. & Ryzhik, L. 2007 Boundary layers and KPP fronts in a cellular flow. Arch. Rat. Mech. Anal. 184, 23–48.Google Scholar
Papanicolaou, G. C. 1995 In Diffusion in Random Media (ed. Keller, J. P.), Surveys in Applied Mathematics, vol. 1, pp. 205–253. Plenum.Google Scholar
Pauls, W. 2006 Transport in cellular flows from the viewpoint of stochastic differential equations. In Proceedings of the 2005 Program on Geophysical Fluid Dynamics (ed. Bühler, O. & Doering, C.), pp. 144–156. Woods Hole Oceanographic Institution.Google Scholar
Rhines, P. B. & Young, W. R. 1983 How rapidly is a passive scalar mixed within closed streamlines. J. Fluid Mech. 133, 133–145.Google Scholar
Rosenbluth, M. N., Berk, H. L., Doxas, I. & Horton, W. 1987 Effective diffusion in laminar convective flows. Phys. Fluids 30, 2636–2647.Google Scholar
Shraiman, B. I. 1987 Diffusive transport in a Rayleigh–Bénard convection cell. Phys. Rev. A 36, 261–267.Google Scholar
Soward, A. M. 1987 Fast dynamo action in a steady flow. J. Fluid Mech. 180, 267–295.CrossRefGoogle Scholar
Taylor, G. I. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219, 186–203.Google Scholar
Touchette, H. 2009 Large deviation approach to statistical mechanics. Phys. Rep. 478, 1–69.Google Scholar
Tsang, Y.-K., Antonsen, T. M. & Ott, E. 2005 Exponential decay of chaotically advected passive scalars in the zero diffusivity limit. Phys. Rev. E 71, 066301.Google Scholar
Tzella, A. & Vanneste, J.2014a Front propagation in cellular flows: a large-deviation approach (in preparation).Google Scholar
Tzella, A. & Vanneste, J.2014b Front propagation in cellular flows for fast reaction and small diffusivity (in preparation).Google Scholar
Xin, J. 2009 An Introduction to Fronts in Random Media. Springer.Google Scholar