Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-19T14:10:25.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Dispersal of buoyancy-driven flow in porous media with inclined baffles

Published online by Cambridge University Press:  08 November 2011

W. J. Rayward-Smith  and
Andrew W. Woods
W. J. Rayward-Smith*
Affiliation:
BP Institute for Multiphase Flow, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
Andrew W. Woods
Affiliation:
BP Institute for Multiphase Flow, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Here we explore the effect of a series of low-permeability tilted baffles on the ascent of a buoyant fluid injected into a porous rock from a linear well, motivated by several industrial processes, particularly CO2 sequestration. We first consider, both theoretically and experimentally, the dynamics associated with flow past an individual inclined baffle; if the incident flux is sufficiently large then a pool of injectate grows beneath the baffle and spills over both ends, partitioning the flux, but otherwise the injectate only flows over the updip end of the baffle, leaving a stagnant zone under the downdip part of the baffle. In a multi-layered system, the flow may then be described using nonlinear recurrence relations based on the flow past an individual baffle. Using this approach, in the particular case in which there is a regular distribution of baffles, we show that, on a scale greater than individual baffles, the flow adjusts to a plume of constant width rising at an angle 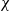to the vertical, which depends on the geometry of the baffles. This constant-width plume may be described by an effective directional permeability 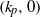at angles 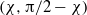to the vertical where we find 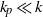, where 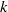is the effective permeability of the regions between baffles. Within the boundaries of this plume the majority of pore space is bypassed. Indeed, the plume-scale effective porosity is largely associated with the pools of injectate which collect beneath each baffle. We show that since the constant-width plume has such a large lateral extent, the total pore space occupied by the plume, per unit height, is larger than for a homogeneous formation. Furthermore, these pools lead to a large surface area between injectate and formation water, which enhances the reaction of the injectate with the formation water. However, we also show that, in steady state, it may be hard to determine this plume-scale effective porosity since the ratio of the effective Darcy speed and the effective interstitial speed of the plume only relates to the porosity of the updip part of these pools, in which the injectate is flowing.

JFM classification

Geophysical and Geological Flows: Gravity currents Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 689 , 25 December 2011 , pp. 517 - 528
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Allen, J. R. L. 1985 Principles of Physical Sedimentology. Allen & Unwin.Google Scholar
2. Arts, R., Eiken, O., Chadwick, A., Zweigel, P., Van Der Meer, L. & Zinszner, B. 2004 Monitoring of injected at Sleipner using time-lapse seismic data. Energy 29, 1383–1392.CrossRefGoogle Scholar
3. Bear, J. 1972 Dynamics of Fluids in Porous Materials. American Elsevier.Google Scholar
4. Braun, C., Helmig, R. & Manthey, S. 2003 Determination of constitutive relationships for two-phase flow processes in heterogeneous porous media with emphasis on the relative permeability-saturation relationship. J. Contam. Hydrol. 67, 47–85.Google Scholar
5. Durlofsky, L. J. 1991 Numerical calculation of equivalent grid block permeability tensors for heterogeneous media. Water Resour. Res. 27, 699–708.CrossRefGoogle Scholar
6. Eames, I. 1999 A hundred years of Hele-Shaw’s analogue computer. Maths Today June 85–88.Google Scholar
7. Eichel, H., Helmig, R., Neuweiler, I. & Cirpka, O. A. 2005 Upscaling of two-phase flow processes in porous media. In Upscaling Multiphase Flow in Porous Media (ed. Das, D. B. & Hassanizadeh, S. M. ). pp. 237–257. Springer.CrossRefGoogle Scholar
8. Golding, M. J., Neufeld, J. A., Hesse, M. A. & Huppert, H. E. 2011 Two-phase gravity currents in porous media. J. Fluid Mech. 678, 248–270.CrossRefGoogle Scholar
9. Green, C. P. & Ennis-King, J. 2010 Effect of vertical heterogeneity on long-term migration of CO2 in saline formations. Transp. Porous Med. 82, 31–47.CrossRefGoogle Scholar
10. Haldorsen, H. H. & Lake, L. W. 1984 A new approach to shale management in field-scale models. Soc. Petrol. Engrs J. 24 (4), 447–457.CrossRefGoogle Scholar
11. Hesse, M. A., Orr, F. M. Jr. & Tchelepi, J. A. 2008 Gravity currents with residual trapping. J. Fluid Mech. 611, 35–60.CrossRefGoogle Scholar
12. Hesse, M. A. & Woods, A. W. 2010 Buoyant dispersal of during geological storage. Geophys. Res. Lett. 37, L01403.CrossRefGoogle Scholar
13. Huppert, H. E. & Woods, A. W. 1995 Gravity-driven flows in porous layers. J. Fluid Mech. 292, 55–69.CrossRefGoogle Scholar
14. Johnson, J. W., Nitao, J. J. & Knauss, K. G. 2004 Reactive transport modelling of storage in saline aquifers to elucidate fundamental processes, trapping mechanisms and sequestration partitioning. Geol. Soc. Spec. Publ. 233, 107–128.CrossRefGoogle Scholar
15. Neufeld, J. A., Hesse, M. A., Riaz, A., Hallworth, M. A., Tchelepi, H. A. & Huppert, H. E. 2010 Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett. 37, L22404.CrossRefGoogle Scholar
16. Neufeld, J. A. & Huppert, H. E. 2009 Modelling carbon dioxide sequestration in layered strata. J. Fluid Mech. 625, 353–370.CrossRefGoogle Scholar
17. Pritchard, D., Woods, A. W. & Hogg, A. J. 2001 On the slow draining of a gravity current moving through a layered permeable medium. J. Fluid Mech. 444, 23–47.CrossRefGoogle Scholar
18. Richardson, J. G., Harris, D. G., Rossen, R. H. & Van Hee, G. 1978 The effect of small, discontinuous shales on oil recovery. J. Petrol. Tech. 30 (11), 1531–1537.CrossRefGoogle Scholar
19. Saadatpoor, E., Bryant, S. L. & Sepehrnoori, K. 2010 New trapping mechanism in carbon sequestration. Trans. Porous Med. 82, 3–17.CrossRefGoogle Scholar
20. Serra, O. 1984 Fundamentals of Well-Log Interpretation. Amsterdam Elsevier.Google Scholar
21. White, C. D. & Barton, M. D. 1999 Translating outcrop data to flow models, with applications to the Ferron sandstone. SPE Res. Evaluation & Engng 2 (4), 341–350.CrossRefGoogle Scholar
22. Woods, A. W. & Farcas, A. 2009 Capillary entry pressure and the leakage of gravity currents through a sloping layered permeable rock. J. Fluid Mech. 618, 361–379.CrossRefGoogle Scholar
23. Yeh, T. C. J., Gelhar, L. W. & Gutjahr, A. L. 1985 Stochastic analysis of unsaturated flow in heterogeneous soils 1–3. Water Resour. Res. 21 (4), 447–471.CrossRefGoogle Scholar