Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-08T21:59:51.475Z Has data issue: false hasContentIssue false
  • English
  • Français

Control of light gas releases in ventilated tunnels

Published online by Cambridge University Press:  10 June 2019

L. Jiang ,
M. Creyssels ,
G. R. Hunt Open the ORCID record for G. R. Hunt [Opens in a new window]  and
P. Salizzoni Open the ORCID record for P. Salizzoni [Opens in a new window]
L. Jiang
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, University of Lyon, CNRS UMR 5509, Ecole Centrale de Lyon, INSA Lyon, Université Claude Bernard, 36 Avenue Guy de Collongue, 69134 Ecully, France
M. Creyssels
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, University of Lyon, CNRS UMR 5509, Ecole Centrale de Lyon, INSA Lyon, Université Claude Bernard, 36 Avenue Guy de Collongue, 69134 Ecully, France
G. R. Hunt
Affiliation:
Department of Engineering, University of Cambridge, Cambridge CB2 1PZ, UK
P. Salizzoni*
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, University of Lyon, CNRS UMR 5509, Ecole Centrale de Lyon, INSA Lyon, Université Claude Bernard, 36 Avenue Guy de Collongue, 69134 Ecully, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The release of buoyant harmful gases within enclosed spaces, such as tunnels and corridors, may engender specific health, industrial and transportation risks. For safety, a simple ventilation strategy for these spaces is to impose a flow along the tunnel, whose velocity is defined as ‘critical’, that confines the front of harmful buoyant gases immediately downstream of the source of emission. Determining the critical velocity as a function of the geometrical and dynamical conditions at the source is a fundamental fluid mechanics problem which has yet to be elucidated; this problem concerns the dynamics of non-Boussinesq releases relating to large differences between the densities of the buoyant and the ambient fluids. We have investigated this problem theoretically, by means of a simplified model of a top-hat plume in a cross-flow, and in complementary experiments by means of tests in a reduced-scale ventilated tunnel, examining releases from circular sources. Experimental results reveal: (i) the existence of two flow regimes depending on the plume Richardson number at the source 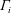$\unicode[STIX]{x1D6E4}_{i}$, one for momentum-dominated releases, 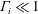$\unicode[STIX]{x1D6E4}_{i}\ll 1$, and a second for buoyancy-dominated releases, 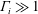$\unicode[STIX]{x1D6E4}_{i}\gg 1$, with a smooth transition between the two; and (ii) the presence of relevant non-Boussinesq effects only for momentum-dominated releases. All these features can be conveniently predicted by the plume-based model, whose validity is, strictly speaking, limited to releases issuing from ‘small’ sources in ‘weak’ ventilation flows. Analytical solutions of the model are generally in good agreement with the experimental data, even for values of the governing parameters that are beyond the range of validity for the model. The solutions aid to clarify the effect of the source radius, and reveal interesting behaviours in the limits 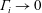$\unicode[STIX]{x1D6E4}_{i}\rightarrow 0$ and 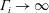$\unicode[STIX]{x1D6E4}_{i}\rightarrow \infty$. These findings support the adoption of simplified models to simulate light gas releases in confined ventilated spaces.

JFM classification

Convection: Plumes/thermals Turbulent Flows: Turbulent convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 872 , 10 August 2019 , pp. 515 - 531
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arya, S. P. S. & Lape, J. F. J. 1990 A comparative study of the different criteria for the physical modelling of buoyant plume rise in a neutral atmosphere. Atmos. Environ. 24, 289–295.Google Scholar
Aubry, T. J., Jelline, A. M., Carazzo, C., Gallo, R., Hatcher, K. & Dunning, J. 2017 A new analytical scaling for turbulent wind-bent plumes: comparison of scaling laws with analog experiments and a new database of eruptive conditions for predicting the height of volcanic plumes. J. Volcanol. Geotherm. Res. 343, 233–251.Google Scholar
Barnett, S. J. 1993 A vertical buoyant jet with high momentum in a long ventilated tunnel. J. Fluid Mech. 252, 279–300.Google Scholar
van den Bremer, T. S. & Hunt, G. R. 2010 Universal solutions for Boussinesq and non-Boussinesq plumes. J. Fluid Mech. 644, 165–192.Google Scholar
Carazzo, G., Kaminski, E. & Tait, S. 2006 The route to self-similarity in turbulent jets and plumes. J. Fluid Mech. 547, 137–148.Google Scholar
Carlotti, P. & Hunt, G. R. 2017 An entrainment model for lazy turbulent plumes. J. Fluid Mech. 811, 682–700.Google Scholar
Craske, J. & van Reeuwijk, M. 2015 Energy dispersion in turbulent jets: Part 1. Direct simulation of steady and unsteady jets. J. Fluid Mech. 763, 500–537.Google Scholar
Craske, J., Salizzoni, P. & van Reeuwijk, M. 2017 The turbulent Prandtl number in a pure plume is 3/5. J. Fluid Mech. 822, 774–790.Google Scholar
Devenish, B. J., Rooney, G. G., Webster, H. N. & Thomson, D. J. 2010 The entrainment rate for buoyant plumes in a crossflow. Boundary-Layer Meteorol. 134, 411–439.Google Scholar
Ezzamel, A.2011 Free and confined buoyant flows. PhD thesis, Imperial College London – Ecole Centrale de Lyon.Google Scholar
Ezzamel, A., Salizzoni, P. & Hunt, G. R. 2015 Dynamical variability of axisymmetric buoyant plumes. J. Fluid Mech. 765, 576–611.Google Scholar
Grant, G. B., Jagger, S. F. & Lea, C. J. 1998 Fires in tunnels. Phil. Trans. R. Soc. Lond. A 356, 2873–2906.Google Scholar
Hewett, T. A., Fay, J. A. & Hoult, D. P. 1971 Laboratory experiments of smokestack plumes in a stable atmosphere. Atmos. Environ. 5 (9), 767–789.Google Scholar
Hoult, D. P., Fay, J. A. & Forney, L. J. 1969 A theory of plume rise compared with field observation. J. Air Pollut. Control Assoc. 19, 585–590.Google Scholar
Hunt, G. R. & Kaye, N. B. 2005 Lazy plumes. J. Fluid Mech. 533, 329–338.Google Scholar
Hunt, J. C. R. 1991 Industrial and environmental fluid mechanics. Annu. Rev. Fluid Mech. 23, 1–41.Google Scholar
Jiang, L., Creyssels, M., Mos, A. & Salizzoni, P. 2018 Critical velocity in ventilated tunnels in the case of fire plumes and densimetric plumes. Fire Safety J. 101, 53–62.Google Scholar
Jirka, G. H. & Harleman, D. R. F. 1979 Stability and mixing of a vertical plane buoyant jet in confined depth. J. Fluid Mech. 94 (02), 275–304.Google Scholar
Kaye, N. B. & Hunt, G. R. 2007 Overturning in a filling box. J. Fluid Mech. 576, 297–323.Google Scholar
Le Clanche, J., Salizzoni, P., Creyssels, M., Mehaddi, R., Candelier, F. & Vauquelin, O. 2014 Aerodynamics of buoyant releases within a longitudinally ventilated tunnel. Exp. Therm. Fluid Sci. 57, 121–127.Google Scholar
Manins, P. C. 1979 Turbulent buoyant convection from a source in a confined region. J. Fluid Mech. 91, 765–781.Google Scholar
Marjanovic, G., Taub, G. N. & Balachandar, S. 2017 On the evolution of the plume function and entrainment in the near-source region of lazy plumes. J. Fluid Mech. 830, 736–759.Google Scholar
Marro, M., Salizzoni, P., Cierco, F. X., Korsakissok, I., Danzi, E. & Soulhac, L. 2014 Plume rise and spread in buoyant releases from elevated sources in the lower atmosphere. Environ. Fluid Mech. 55, 50–57.Google Scholar
Michaux, G. & Vauquelin, O. 2008 Solutions for turbulent buoyant plumes rising from circular sources. Phys. Fluids 20, 066601.Google Scholar
Morton, B. R., Taylor, G. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Oka, Y. & Atkinson, G. T. 1995 Control of smoke flow in tunnel fires. Fire Safety J. 25, 305–322.Google Scholar
van Reeuwijk, M., Salizzoni, P., Hunt, G. R. & Craske, J. 2016 Turbulent transport and entrainment in jets and plumes: A DNS study. Phys. Rev. Fluids 1, 074301.Google Scholar
Ricou, F. P. & Spalding, D. B. 1961 Measurements of entrainment by axisymmetrical turbulent jets. J. Fluid Mech. 11, 21–32.Google Scholar
Robins, A. G., Apsley, D. D., Carruthers, D. J., McHugh, C. A. & Dyster, S. J.2009 Plume rise model specification, Tech. Rep., University of Surrey, National Power and CERC.Google Scholar
Rooney, G. G. & Linden, P. F. 1996 Similarity considerations for non-Boussinesq plumes in an unstratified environment. J. Fluid Mech. 318, 237–250.Google Scholar
Salizzoni, P., Creyssels, M., Jiang, L., Mos, A., Mehaddi, R. & Vauquelin, O. 2018 Influence of source conditions and heat losses on the upwind back-layering flow in a longitudinally ventilated tunnel. Intl J. Heat Mass Transfer 117, 143–153.Google Scholar
Suzuki, Y. J. & Koyaguchi, T. 2015 Effects of wind on entrainment efficiency in volcanic plumes. J. Geophys. Res. 120 (9), 6122–6140.Google Scholar
Thomas, P. H.1968 The movement of smoke in horizontal passages against an air flow, Fire Research Note 723, Fire Research Station.Google Scholar
Vauquelin, O. 2008 Experimental simulations of fire-induced smoke control in tunnels using a helium reduced scale model: principle, limitations, results and future. Tunn. Undergr. Sp. Technol. 23, 171–178.Google Scholar
Woodhouse, M. J., Hogg, A. J., Phillips, J. C. & Sparks, R. S. J. 2013 Interaction between volcanic plumes and wind during the 2010 Eyjafjallajökull eruption, Iceland. J. Geophys. Res. 118 (1), 92–109.Google Scholar
Woods, A. W. 1997 A note on non-Boussinesq plumes in an incompressible stratified environment. J. Fluid Mech. 345, 347–356.Google Scholar
Wu, Y. & Bakar, M. Z. A. 2000 Control of smoke flow in tunnel fires using longitudinal ventilation systems – a study of the critical velocity. Fire Safety J. 35 (4), 363–390.Google Scholar