Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ng, Henry C.-H.
Collignon, Emile
Poole, Robert J.
and
Dennis, David J. C.
2021.
Energetic motions in turbulent partially filled pipe flow.
Physics of Fluids,
Vol. 33,
Issue. 2,
Nevolin, A M
Osipov, L E
and
Plotnikov, L V
2021.
Influence of gas flow turbulence scale on heat exchange intensity in a long smooth pipe.
Journal of Physics: Conference Series,
Vol. 1867,
Issue. 1,
p.
012001.
Duan, Yanchong
Zhong, Qiang
Wang, Guiquan
Chen, Qigang
Wang, Fujun
and
Li, Danxun
2021.
Additional spanwise vortices near the free surface in open channel flows.
Journal of Fluid Mechanics,
Vol. 924,
Issue. ,
Peruzzi, C.
Vettori, D.
Poggi, D.
Blondeaux, P.
Ridolfi, L.
and
Manes, C.
2021.
On the influence of collinear surface waves on turbulence in smooth-bed open-channel flows.
Journal of Fluid Mechanics,
Vol. 924,
Issue. ,
Camporeale, Carlo
Cannamela, Fabio
Canuto, Claudio
and
Manes, Costantino
2021.
Stability analysis of open-channel flows with secondary currents.
Journal of Fluid Mechanics,
Vol. 927,
Issue. ,
Duan, Yanchong
Zhong, Qiang
Wang, Guiquan
Zhang, Peng
and
Li, Danxun
2021.
Contributions of different scales of turbulent motions to the mean wall-shear stress in open channel flows at low-to-moderate Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 918,
Issue. ,
Proust, Sébastien
Berni, Céline
and
Nikora, Vladimir I.
2022.
Shallow mixing layers over hydraulically smooth bottom in a tilted open channel.
Journal of Fluid Mechanics,
Vol. 951,
Issue. ,
Chen, Yue
Yang, Wenjun
Lin, Haili
Li, Bin
and
Jing, Siyu
2022.
Modified kernel density-based algorithm for despiking acoustic Doppler velocimeter data.
Measurement,
Vol. 204,
Issue. ,
p.
112043.
Yan, Zili
Duan, Yanchong
Zhu, Dejun
and
Li, Danxun
2022.
Characteristics of very-large-scale motions in gradually varied open-channel flows upstream of a run-of-river dam.
Physics of Fluids,
Vol. 34,
Issue. 9,
Khan, Mohammad Amir
Sharma, Nayan
Aamir, Mohammad
Pandey, Manish
Garg, Rishav
and
Pourshahbaz, Hanif
2022.
Water Resource Modeling and Computational Technologies.
Vol. 7,
Issue. ,
p.
483.
Qi, Wen-Gang
Liu, Jun
Gao, Fu-Ping
Li, Biao
and
Chen, Qi-Gang
2022.
Quantifying the spatiotemporal evolution of the turbulent horseshoe vortex in front of a vertical cylinder.
Physics of Fluids,
Vol. 34,
Issue. 1,
Das, S.
Balachandar, R.
and
Barron, R.M.
2022.
Generation and characterization of fully developed state in open channel flow.
Journal of Fluid Mechanics,
Vol. 934,
Issue. ,
Yao, Jie
Chen, Xi
and
Hussain, Fazle
2022.
Direct numerical simulation of turbulent open channel flows at moderately high Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 953,
Issue. ,
Fu, Jiahao
He, Guojian
Huang, Lei
Dey, Subhasish
and
Fang, Hongwei
2023.
Swaying motions of submerged flexible vegetation.
Journal of Fluid Mechanics,
Vol. 971,
Issue. ,
Pirozzoli, Sergio
2023.
Searching for the log law in open channel flow.
Journal of Fluid Mechanics,
Vol. 971,
Issue. ,
Shen, Ying
Yang, Shengfa
and
Liu, Jie
2023.
Characteristics of Very Large-Scale Motions in Rough-Bed Open-Channel Flows.
Water,
Vol. 15,
Issue. 7,
p.
1433.
2023.
Statistical behavior of wall-attached motions in open- and closed-channel flows via direct numerical simulation.
Physics of Fluids,
Vol. 35,
Issue. 4,
Zampiron, Andrea
Cameron, Stuart M.
and
Nikora, Vladimir
2023.
On application of empirical mode decomposition for turbulence analysis in open-channel flows.
Journal of Hydraulic Research,
Vol. 61,
Issue. 5,
p.
788.
Yan, Zili
Zhu, Dejun
and
Li, Danxun
2023.
The vitality of very-large-scale motions upstream of an overflow structure.
AIP Advances,
Vol. 13,
Issue. 3,
Liu, Yixun
Liu, Chun-Ho
Brasseur, Guy P.
and
Chao, Christopher Y.H.
2023.
Empirical mode decomposition of the atmospheric flows and pollutant transport over real urban morphology.
Environmental Pollution,
Vol. 331,
Issue. ,
p.
121858.
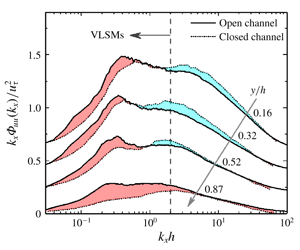
 $20h$ (
$20h$ ( $h$ is water depth), which is comparable to that in pipe and closed channels while smaller than that in rough-walled open channels, and they are shown to make a great contribution to turbulence statistics with over 50 % of streamwise turbulence intensity, Reynolds shear stress and negative net force coming from VLSMs in the outer layer. Compared with other wall-bounded flows, VLSMs maintain higher strength in the outer layer of open channel flows with non-negligible strength even in the near surface region (
$h$ is water depth), which is comparable to that in pipe and closed channels while smaller than that in rough-walled open channels, and they are shown to make a great contribution to turbulence statistics with over 50 % of streamwise turbulence intensity, Reynolds shear stress and negative net force coming from VLSMs in the outer layer. Compared with other wall-bounded flows, VLSMs maintain higher strength in the outer layer of open channel flows with non-negligible strength even in the near surface region ( $y\sim >0.8h$), indicating that the free surface seems to sustain/promote VLSMs. This strength difference of VLSMs closely relates to the TKE redistribution and smaller wake strength of the mean velocity in the outer layer of open channel flows. The higher streamwise turbulence intensity is mainly contributed from the higher strength of VLSMs therein. The decelerating role of VLSMs combining with their higher strength is vital for shaping the mean velocity profile, which therefore is speculated to make a great contribution to the smaller wake strength phenomenon.
$y\sim >0.8h$), indicating that the free surface seems to sustain/promote VLSMs. This strength difference of VLSMs closely relates to the TKE redistribution and smaller wake strength of the mean velocity in the outer layer of open channel flows. The higher streamwise turbulence intensity is mainly contributed from the higher strength of VLSMs therein. The decelerating role of VLSMs combining with their higher strength is vital for shaping the mean velocity profile, which therefore is speculated to make a great contribution to the smaller wake strength phenomenon.