Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-18T21:15:47.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Collision statistics of inertial particles in two-dimensional homogeneous isotropic turbulence with an inverse cascade

Published online by Cambridge University Press:  19 March 2014

Ryo Onishi  and
J. C. Vassilicos
Ryo Onishi*
Affiliation:
Earth Simulator Centre, Japan Agency for Marine–Earth Science and Technology, 3173-25 Showa-machi, Kanazawa-ku, Yokohama, Kanagawa 236-0001, Japan
J. C. Vassilicos
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This study investigates the collision statistics of inertial particles in inverse-cascading two-dimensional (2D) homogeneous isotropic turbulence by means of a direct numerical simulation (DNS). A collision kernel model for particles with small Stokes number (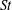$\mathit{St}$) in 2D flows is proposed based on the model of Saffman & Turner (J. Fluid Mech., vol. 1, 1956, pp. 16–30) (ST56 model). The DNS results agree with this 2D version of the ST56 model for 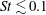$\mathit{St}\lesssim 0.1$. It is then confirmed that our DNS results satisfy the 2D version of the spherical formulation of the collision kernel. The fact that the flatness factor stays around 3 in our 2D flow confirms that the present 2D turbulent flow is nearly intermittency-free. Collision statistics for 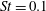$\mathit{St}= 0.1$, 0.4 and 0.6, i.e. for 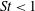$\mathit{St}<1$, are obtained from the present 2D DNS and compared with those obtained from the three-dimensional (3D) DNS of Onishi et al. (J. Comput. Phys., vol. 242, 2013, pp. 809–827). We have observed that the 3D radial distribution function at contact (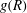$g(R)$, the so-called clustering effect) decreases for 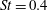$\mathit{St}= 0.4$ and 0.6 with increasing Reynolds number, while the 2D 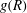$g(R)$ does not show a significant dependence on Reynolds number. This observation supports the view that the Reynolds-number dependence of 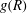$g(R)$ observed in three dimensions is due to internal intermittency of the 3D turbulence. We have further investigated the local 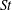$\mathit{St}$, which is a function of the local flow strain rates, and proposed a plausible mechanism that can explain the Reynolds-number dependence of 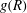$g(R)$. Meanwhile, 2D stochastic simulations based on the Smoluchowski equations for 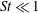$\mathit{St}\ll 1$ show that the collision growth can be predicted by the 2D ST56 model and that rare but strong events do not play a significant role in such a small-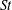$\mathit{St}$ particle system. However, the probability density function of local 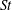$\mathit{St}$ at the sites of colliding particle pairs supports the view that powerful rare events can be important for particle growth even in the absence of internal intermittency when 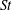$\mathit{St}$ is not much smaller than unity.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 745 , 25 April 2014 , pp. 279 - 299
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abrahamson, J. 1975 Collision rates of small particles in a vigorously turbulent fluid. Chem. Engng Sci. 30 (11), 1371–1379.Google Scholar
Allen, M. P. & Tildesley, D. J. 1987 Computer Simulation of Liquids. Oxford University Press.Google Scholar
Ayala, O., Rosa, B. & Wang, L.-P. 2008 Effects of turbulence on the geometric collision rate of sedimenting droplets. Part 2. Theory and parameterization. New J. Phys. 10 (7), 075016.Google Scholar
Blyth, A. M. 1993 Entrainment in cumulus clouds. J. Appl. Meteorol. 32, 626–641.Google Scholar
Bordas, R., Hagemeier, T., Wunderlich, B. & Thevenin, D. 2011 Droplet collisions and interaction with the turbulent flow within a two-phase wind tunnel. Phys. Fluids 23, 085105.Google Scholar
Chen, L., Goto, S. & Vassilicos, J. C. 2006 Turbulent clustering of stagnation points and inertial particles. J. Fluid Mech. 553, 143–154.CrossRefGoogle Scholar
Chun, J., Koch, D. L., Rani, S. L., Ahluwalia, A. & Collins, L. R. 2005 Clustering of aerosol particles in isotropic turbulence. J. Fluid Mech. 536, 219–251.CrossRefGoogle Scholar
Coleman, S. W. & Vassilicos, J. C. 2009 A unified sweep–stick mechanism to explain particle clustering in two- and three-dimensional homogeneous, isotropic turbulence. Phys. Fluids 21 (11), 113301.Google Scholar
Dallas, V. & Vassilicos, J. C. 2011 Rapid growth of cloud droplets by turbulence. Phys. Rev. E 84, 046315.Google Scholar
Derevyanko, S., Falkovich, G. & Turitsyn, S. 2008 Evolution of non-uniformly seeded warm clouds in idealized turbulent conditions. New J. Phys. 10, 075019.Google Scholar
Faber, T. & Vassilicos, J. C. 2010 Acceleration-based classification and evolution of fluid flow structures in two-dimensional turbulence. Phys. Rev. E 82, 026312.Google Scholar
Falkovich, G. & Pumir, A. 2007 Sling effect in collisions of water droplets in turbulent clouds. J. Atmos. Sci. 64 (12), 4497–4505.Google Scholar
Franklin, C. N., Vaillancourt, P. A. & Yau, M. K. 2007 Statistics and parameterizations of the effect of turbulence on the geometric collision kernel of cloud droplets. J. Atmos. Sci. 64 (3), 938–954.Google Scholar
Goto, S., Osborne, D. R., Vassilicos, J. C. & Haigh, J. D. 2005 Acceleration statistics as measures of statistical persistence of streamlines in isotropic turbulence. Phys. Rev. E 71, 015301.CrossRefGoogle ScholarPubMed
Goto, S. & Vassilicos, J. C. 2004 Particle pair diffusion and persistent streamline topology in two-dimensional turbulence. New J. Phys. 6, 65.Google Scholar
Grabowski, W. W. & Wang, L.-P. 2009 Diffusional and accretional growth of water drops in a rising adiabatic parcel: effects of the turbulent collision kernel. Atmos. Chem. Phys. 9, 2335–2353.Google Scholar
Grabowski, W. W. & Wang, L.-P. 2013 Growth of cloud droplets in a turbulent environment. Annu. Rev. Fluid Mech. 45, 293–324.Google Scholar
Krueger, S. K., Su, C. W. & McMurtry, P. A. 1997 Modelling entrainment and finescale mixing in cumulus clouds. J. Atmos. Sci. 54 (23), 2697–2712.2.0.CO;2>CrossRefGoogle Scholar
Lu, J., Nordsiek, H., Saw, E. W. & Shaw, R. A. 2010 Clustering of charged inertial particles in turbulence. Phys. Rev. Lett. 104 (18), 184505.CrossRefGoogle ScholarPubMed
MacPherson, J. I. & Isaac, G. A. 1977 Turbulent characteristics of some Canadian cumulus clouds. J. Appl. Meteorol. 16, 81–90.2.0.CO;2>CrossRefGoogle Scholar
Maxey, M. R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174, 441–465.Google Scholar
Onishi, R.2005 Numerical simulations of chemical reaction and droplet growth in environmental turbulent flows. PhD thesis, Kyoto University.Google Scholar
Onishi, R., Takagi, H., Takahashi, K. & Komori, S. 2006 Turbulence effects on cloud droplet collisions in mesoscale convective clouds. In Turbulence, Heat and Mass Transfer (ed. Hanjaric, K., Nagano, Y. & Jakirlic, S.), vol. 5, pp. 709–712. Begell House Inc.Google Scholar
Onishi, R., Takahashi, K. & Komori, S. 2009 Influence of gravity on collisions of monodispersed droplets in homogeneous isotropic turbulence. Phys. Fluids 21, 125108.Google Scholar
Onishi, R., Takahashi, K. & Komori, S. 2011 High-resolution simulations for turbulent clouds developing over the ocean. In Gas Transfer at Water Surfaces (ed. Komori, S., McGillis, W. & Kurose, R.), vol. 6, pp. 582–592. Kyoto University Press.Google Scholar
Onishi, R., Takahashi, K. & Vassilicos, J. C. 2013 An efficient parallel simulation of interacting inertial particles in homogeneous isotropic turbulence. J. Comput. Phys. 242, 809–827.Google Scholar
Rosa, B., Parishani, H., Ayala, O., Grabowski, W. & Wang, L.-P. 2013 Kinematic and dynamic collision statistics of cloud droplets from high-resolution simulations. New J. Phys. 15, 045032.Google Scholar
Saffman, P. G. & Turner, J. S. 1956 On the collision of drops in turbulent clouds. J. Fluid Mech. 1 (1), 16–30.CrossRefGoogle Scholar
Saw, E. W., Shaw, R. A., Ayyalasomayajula, S., Chuang, P. Y. & Gylfason, A. 2008 Inertial clustering of particles in high-Reynolds-number turbulence. Phys. Rev. Lett. 100 (21), 214501.Google Scholar
Sidin, R. S. R., Ijzermans, R. H. A. & Reeks, M. W. 2009 A Lagrangian approach to droplet condensation in atmospheric clouds. Phys. Fluids 21 (10), 106603.Google Scholar
Siebert, H., Lehmann, K. & Wendisch, M. 2006 Observations of small-scale turbulence and energy dissipation rates in the cloudy boundary layer. J. Atmos. Sci. 63, 1451–1466.Google Scholar
Sundaram, S. & Collins, L. R. 1996 Numerical considerations in simulating a turbulent suspension of finite-volume particles. J. Comput. Phys. 124 (2), 337–350.CrossRefGoogle Scholar
Sundaram, S. & Collins, L. R. 1997 Collision statistics in an isotropic particle-laden turbulent suspension. Part 1. Direct numerical simulations. J. Fluid Mech. 335, 75–109.Google Scholar
Tabeling, P. 2002 Two-dimensional turbulence: a physicist approach. Phys. Rep. 362, 1–62.Google Scholar
Taylor, G. I. 1935 Statistical theory of turbulence. Proc. R. Soc. Lond. A 151, 421–444.CrossRefGoogle Scholar
Van Den Heever, S. C. & Cotton, W. R. 2007 Urban aerosol impacts on downwind convective storms. J. Appl. Meteorol. Climatol. 46 (6), 828–850.CrossRefGoogle Scholar
Wang, L.-P., Rosa, B., Gao, H., He, G. & Jin, G. 2009 Turbulent collision of inertial particles: point-particle based, hybrid simulations and beyond. Int. J. Multiphase Flow 35 (9), 854–867.Google Scholar
Wang, L.-P., Wexler, A. S. & Zhou, Y. 1998a On the collision rate of small particles in isotropic turbulence. I. Zero-inertia case. Phys. Fluids 10, 266–276.Google Scholar
Wang, L.-P., Wexler, A. S. & Zhou, Y. 1998b Statistical mechanical descriptions of turbulent coagulation. Phys. Fluids 10, 2647–2651.Google Scholar
Wang, L.-P., Wexler, A. S. & Zhou, Y. 2000 Statistical mechanical description and modelling of turbulent collision of inertial particles. J. Fluid Mech. 415, 117–153.Google Scholar
Xue, Y., Wang, L.-P. & Grabowski, W. W. 2008 Growth of cloud droplets by turbulent collision–coalescence. J. Atmos. Sci. 65 (2), 331–356.CrossRefGoogle Scholar
Yin, Y., Levin, Z., Reisin, T. G. & Tzivion, S. 2000 The effects of giant cloud condensation nuclei on the development of precipitation in convective clouds—a numerical study. Atmos. Res. 53 (1–3), 91–116.CrossRefGoogle Scholar
Yoshimatsu, K., Okamoto, N., Schneider, K., Kaneda, Y. & Farge, M. 2009 Intermittency and scale-dependent statistics in fully developed turbulence. Phys. Rev. E 79 (2), 026303.Google Scholar
Zaichik, L. & Alipchenkov, V. 2009 Statistical models for predicting pair dispersion and particle clustering in isotropic turbulence and their applications. New J. Phys. 11, 103018.Google Scholar
Zaichik, L., Simonin, O. & Alipchenkov, V. 2003 Two statistical models for predicting collision rates of inertial particles in homogeneous isotropic turbulence. Phys. Fluids 15, 2995–3005.Google Scholar
Zhou, Y., Wexler, A. S. & Wang, L.-P. 2001 Modelling turbulent collision of bidisperse inertial particles. J. Fluid Mech. 433, 77–104.Google Scholar