Published online by Cambridge University Press: 01 February 2008
Collective diffusivity in a suspension of rigid particles in steady linear viscous flows is evaluated by investigating the dynamics of the time correlation of long-wavelength density fluctuations. In the absence of hydrodynamic interactions between suspended particles in a dilute suspension of identical hard spheres, closed-form asymptotic expressions for the collective diffusivity are derived in the limits of low and high Péclet numbers, where the Péclet number 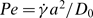 with
with 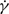 being the shear rate and D0 = kBT/6πη a is the Stokes–Einstein diffusion coefficient of an isolated sphere of radius a in a fluid of viscosity η. The effect of hydrodynamic interactions is studied in the analytically tractable case of weakly sheared (Pe ≪ 1) suspensions.
being the shear rate and D0 = kBT/6πη a is the Stokes–Einstein diffusion coefficient of an isolated sphere of radius a in a fluid of viscosity η. The effect of hydrodynamic interactions is studied in the analytically tractable case of weakly sheared (Pe ≪ 1) suspensions.
For strongly sheared suspensions, i.e. at high Pe, in the absence of hydrodynamics the collective diffusivity Dc = 6 Ds∞, where Ds∞ is the long-time self-diffusivity and both scale as 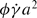 , where φ is the particle volume fraction. For weakly sheared suspensions it is shown that the leading dependence of collective diffusivity on the imposed flow is proportional to D0 φPeÊ, where Ê is the rate-of-strain tensor scaled by
, where φ is the particle volume fraction. For weakly sheared suspensions it is shown that the leading dependence of collective diffusivity on the imposed flow is proportional to D0 φPeÊ, where Ê is the rate-of-strain tensor scaled by 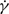 , regardless of whether particles interact hydrodynamically. When hydrodynamic interactions are considered, however, correlations of hydrodynamic velocity fluctuations yield a weakly singular logarithmic dependence of the cross-gradient-diffusivity on k at leading order as ak → 0 with k being the wavenumber of the density fluctuation. The diagonal components of the collective diffusivity tensor, both with and without hydrodynamic interactions, are of O(φPe2), quadratic in the imposed flow, and finite at k = 0.
, regardless of whether particles interact hydrodynamically. When hydrodynamic interactions are considered, however, correlations of hydrodynamic velocity fluctuations yield a weakly singular logarithmic dependence of the cross-gradient-diffusivity on k at leading order as ak → 0 with k being the wavenumber of the density fluctuation. The diagonal components of the collective diffusivity tensor, both with and without hydrodynamic interactions, are of O(φPe2), quadratic in the imposed flow, and finite at k = 0.
At moderate particle volume fractions, 0.10 ≤ φ ≤ 0.35, Brownian Dynamics (BD) numerical simulations in which there are no hydrodynamic interactions are performed and the transverse collective diffusivity in simple shear flow is determined via time evolution of the dynamic structure factor. The BD simulation results compare well with the derived asymptotic estimates. A comparison of the high-Pe BD simulation results with available experimental data on collective diffusivity in non-Brownian sheared suspensions shows a good qualitative agreement, though hydrodynamic interactions prove to be important at moderate concentrations.