Capillary ripples in thin viscous films

Abstract

Capillary ripples in thin viscous films are important features of coating and lubrication flows. Here, we present experiments based on digital holographic microscopy, measuring with nanoscale resolution the morphology of capillary ripples ahead of a viscous drop spreading on a prewetted surface. Our experiments reveal that upon increasing the spreading velocity, the amplitude of the ripples first increases and subsequently decreases. Above a critical spreading velocity, the ripples even disappear completely and this transition is accompanied by a divergence of the ripple wavelength. These observations are explained quantitatively using linear wave analysis, beyond the usual lubrication approximation, illustrating that new phenomena arise when the capillary number becomes of the order of unity.

1 Introduction

Visco-capillary ripples are common features of free-surface flows involving thin viscous films. A prime example of such ripples is given by long bubbles moving in a narrow tube that are separated from the wall by a thin lubrication layer, known as Bretherton bubbles (Bretherton 1961). While the interface shape is monotonic at the bubble’s advancing side, the thin film at the rear exhibits steady capillary waves, that are co-moving with the bubble. Such ripples are found in many other flow phenomena, for example in dip-coating processes, for both plunging and withdrawing plates (Wilson 1982; Snoeijer et al. 2008; Maleki et al. 2011), spreading droplets on a prewetted film (Tanner 1979; Tuck & Schwartz 1990; Cormier et al. 2012; Bergemann, Juel & Heil 2018; Teisala et al. 2018), dewetting fronts (Fetzer et al. 2006; Snoeijer & Eggers 2010) and levelling of capillary films (McGraw et al. 2012; Salez et al. 2012; Ilton et al. 2016). Understanding capillary ripples is important in various fields of applications such as spray coating and ink-jet and 3D printing, where droplets are deposited on either a dry or a wet surface. In coating problems (Ruschak 1985; Weinstein & Ruschak 2004), the ripples dictate the boundary conditions when small-scale flow properties determine far-field flow conditions (Bretherton 1961; Giavedoni & Saita 1999; Taroni et al. 2012). For forced wetting transitions, they give rise to intricate oscillatory bifurcation scenarios (Ziegler, Snoeijer & Eggers 2009; Köpf & Thiele 2014; Lin et al. 2016). In the context of dewetting polymer films, the shape of a ‘dimple’ was even used to quantify the presence of slip (Jacobs, Herminghaus & Mecke 1998; Fetzer et al. 2007; Bäumchen & Jacobs 2010), and thus served as a tool to infer material properties. Visco-capillary ripples can provide information about a flow or a fluid that is otherwise not readily accessed, such as the (nano-)rheological fingerprint of a material (Bäumchen et al. 2012).

The emergence of capillary ripples can be understood from the lubrication equation for thin films. The gradient of capillary pressure, driving the flow, involves the derivative of the curvature, and hence third-order spatial derivatives of the free-surface profile. These high-order derivatives are responsible for the ripples, as they lead to modes of complex wavenumbers and hence (exponentially damped) oscillatory shapes. Indeed, ripples do not appear in gravity-driven flows, for which the pressure gradient involves only the first spatial derivative of the film profile (Huppert 1982). As an illustrative example, we quote here the levelling of a sharp step in film thickness. The gravitational levelling is described by a diffusion-like equation that broadens the step along monotonic profiles, whereas capillary levelling gives rise to undulated profiles (McGraw et al. 2012).

Figure 1. (a) Sketch of the problem: a viscous drop is placed on a thin film of the same fluid and spreads (dimensions not to scale). The magnified view corresponds to the (numerical) solution of the one-dimensional lubrication equation, as presented by Tuck & Schwartz (1990). (b,c) Examples of experimentally obtained profiles, for $Ca=0.0125$ , where a distinct capillary ripple is observed (b), and for $Ca=0.3562$ , where no ripple occurs (c). The red lines indicate the interface profile that can be resolved by DHM (see § 2.1), whereas the grey dashed lines indicate noisy data. In all panels, the arrow shows the direction of the motion and the blue dashed-dotted line indicates the prewetted film thickness.

The theoretical coverage of capillary ripples in these studies is extensive, but several of the presented scenarios have yet to be confirmed experimentally. In this paper we experimentally study the prototypical example of a viscous drop spreading over a film of the same liquid (see figure 1 a). Using digital holographic microscopy (DHM), we quantify the visco-capillary ripples close to the ‘contact line’, where the front of the droplet connects to the prewetted film. Typical experimental results are shown in figure 1(b,c). The analysis of this problem using lubrication theory goes back to pioneering works of Tanner (1979) and Tuck & Schwartz (1990). In the limit where the drops are asymptotically large compared to the film thickness, the dimple is predicted to exhibit a universal profile (inset of figure 1 a) which also plays a key role in the description of dewetting fronts (Snoeijer & Eggers 2010). An interesting characteristic of this solution is that the minimal film thickness $h_{min}$ , compared to the film thickness $h_{\infty }$ , exhibits a significant depression $h_{min}/h_{\infty }\approx 0.82$ , as reported by Tanner (1979) and Tuck & Schwartz (1990).

Here, we show that the dimples can be less pronounced than the asymptotic value of $h_{min}/h_{\infty }\approx 0.82$ (e.g. see figure 1 b), and exhibit a non-trivial dependence on spreading velocity. Remarkably, the oscillations even disappear at both low and high spreading velocities: the ripples give way to a monotonic approach of the prewetted film (figure 1 c). The experiments are interpreted using a linear wave analysis, closely following theoretical work on generic coating flows by Taroni et al. (2012). At high velocity, it is shown that ripples disappear due to the effect of large capillary numbers, i.e. beyond the lubrication hypothesis. The wavelengths are found to diverge at a critical speed, in agreement with theory. At low velocity, we discuss the effect of gravity and the importance of separation of length scales.

2 Experiments

2.1 Materials and methods

A schematic of the experimental set-up is given in figure 2(a). Using a needle, we deposit an oil droplet on a prewetted oil surface. The fluid used in the experiments is a silicone oil of viscosity $\unicode[STIX]{x1D702}=12.125~\text{Pa}~\text{s}$ . The surface tension of the material is $\unicode[STIX]{x1D6FE}=0.021~\text{N}~\text{m}^{-1}$ and the density is $\unicode[STIX]{x1D70C}=972~\text{kg}~\text{m}^{-3}$ . Thin films of different thicknesses in the range $15~\unicode[STIX]{x03BC}\text{m}\leqslant h_{\infty }\leqslant 65~\unicode[STIX]{x03BC}\text{m}$ were acquired by spin-coating the silicone oil on cleaned glass slides. The height of the films was measured with a spectroscope at multiple locations to ensure flatness. We could control the spreading velocity by changing the rate of extrusion of the syringe pump (Harvard PHD ULTRA™ 70-3006) connected to the needle. When extruding, we ensured that the droplets were sufficiently large so that the presence of the needle had no influence on the spreading dynamics. In those cases, the height of the droplets is of the same order of magnitude as the capillary length, $\ell _{\unicode[STIX]{x1D6FE}}=\sqrt{\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D70C}g}\sim \mathit{O}(1~\text{mm})$ , and much larger than the film thickness. To achieve low spreading velocities, we deposited a droplet manually or with the syringe pump on the film. Without further extrusion, the droplets spread spontaneously because of capillary action, as well as their weight. Due to the high viscosity of the chosen silicone oil, some of the experiments take more than 30 h. The spreading velocity slowly decreases with time. However, in our analysis we assume quasi-steady dynamics, which is well in line with classical work (e.g. Hocking 1983). Our results will later confirm that this assumption is indeed valid. In order to measure the wavelengths in the lower $Ca$ range, we performed imaging at frame rates as low as 0.001 Hz and made use of a low-magnification lens ( $\times 1.25$ ), which provided a wider field of view. At very small velocities, the height of the droplet can become comparable to the height of the prewetted film. The spreading velocity, $v$ , was measured by dividing the distance the first extremum travelled between frames by the time passed between the frames. Once the ripples disappeared, we opted to measure the front velocity by setting the travelling point at the first measured height line of the phase image (e.g. see figure 2 c).

Figure 2. (a) The experimental set-up for investigations into the undulating surface of a thin film at the edge of a moving droplet. Droplets were gently placed (or extruded) on a thin layer of the same liquid. Holograms are captured from above using reflection DHM. Examples of phase images are shown for (b) $Ca=0.0125$ and (c) $Ca=0.3562$ . In (b,c), the diagonal arrows indicate the direction of motion. Along this diagonal, the height profiles seen in figure 1 are extracted. The phase images show noisy parts in the lower left-hand corners, where the surface slope of the droplet is too steep to be resolved. These parts correspond to the dashed lines in the profiles of figure 1. The blue arrows indicate the direction of spreading.

To measure the ripples, we imaged the droplets from above, where the front of the droplet invades a fixed field of view. Our main tool of measurement was a reflection digital holographic microscope (LynceeTec DHM^®-R1000). The device records holograms, created through laser interference, with a CCD (charge coupled device) camera (Mikrotron EoSens 4CXP). From these holograms, one can numerically reconstruct intensity and phase information. Herein, the phase information provides the height profile of the thin film. Figure 2(b,c) shows phase images corresponding to the reconstructed height profiles shown in figure 1(b,c). Digital holographic microscopy can offer a high resolution (of sub-nanometre) in line with the laser beam and in contrast to some other optical systems, such as confocal microscopy, does not require scanning motion (that limits the observable time scales of a phenomenon as well as the resolution). Furthermore, DHM is non-invasive, as compared to, for example, atomic force microscopy that requires physical contact between the probe and the sample. This presents another advantage of DHM for the investigation of thin-film flows. A disadvantage of the system for profilometry of thin films is its limitations for non-shallow surfaces. For a given laser, the maximum detectable slope depends on the numerical aperture of the objective lens used. Above a given slope, the reflected beam is no longer collected by the lens and hence, instead of interference fringes, noisy speckle-like patterns form. Examples of this limitation are shown in figure 2(b,c), where the data corresponding to the dashed-grey part of the profiles are noise. Therefore, depending on the application, one should find an optimal setting, considering the field of view, the lateral resolution and the slope of interest. For a more detailed description of DHM, see e.g. Kim (2010).

In our system, the vertical resolution in line with the laser beam is ${\sim}1~\text{nm}$ . The lateral resolution, limited by the used objective lens, ranges between $2.85~\unicode[STIX]{x03BC}\text{m}$ ( $\times 5$ magnification) and $8.5~\unicode[STIX]{x03BC}\text{m}$ ( $\times 1.25$ magnification). We record the holograms from 5 frames per second down to 1 frame every 15 min. The maximum slope varies between $3.4^{\circ }$ ( $\times 5$  magnification) and $1.1^{\circ }$ ( $\times 1.25$ magnification). The configurations above provide a suitable imaging set-up for our study, as all quantities of interest could be well resolved.

2.2 Amplitude and wavelength of the ripples

We extract two main features from the experimentally measured height profiles: the minimum height $h_{min}$ and the ripple wavelength $\unicode[STIX]{x1D706}$ . Note that the waves are exponentially damped, so that the position of the second minimum is difficult to determine experimentally. We therefore measure half of the wavelength, $\unicode[STIX]{x1D706}/2$ , from the distance between the minimum and the first maximum (see figure 1 b). Our prime interest is to investigate how $h_{min}$ and $\unicode[STIX]{x1D706}$ evolve as functions of the capillary number $Ca=\unicode[STIX]{x1D702}v/\unicode[STIX]{x1D6FE}$ .

Figure 3(a) shows the normalised film thickness $h_{min}/h_{\infty }$ versus the capillary number. Different symbols correspond to different film thickness, $h_{\infty }$ . The minimum film height in our experiments comes close to the predicted asymptotic value of $0.82h_{\infty }$ , but stays above that for all $Ca$ . The deepest dimples roughly correspond to $h_{min}/h_{\infty }\approx 0.85$ around $Ca\approx 2\times 10^{-3}$ . Intriguingly, however, the dimple height exhibits a non-monotonic dependence with $Ca$ . The ripples tend to flatten for both increasing and decreasing spreading velocities, with $h_{min}/h_{\infty }\rightarrow 1$ . This trend is observed for all film thicknesses.

A remarkable feature appears at large speeds. Namely, we can clearly identify a critical capillary number, $Ca\approx 0.295\pm 0.042$ (the grey zone in figure 3), at which the undulations suddenly disappear. At larger capillary numbers the droplet monotonically joins the viscous film, and no ripples are observed. This transition can also be observed in one single experiment, if the contact line velocity is high in the beginning and, during the spreading of the droplet, will drop below the threshold. Examples of an undulated and a monotonic contact line area can be found in the profiles in figure 1(b,c).

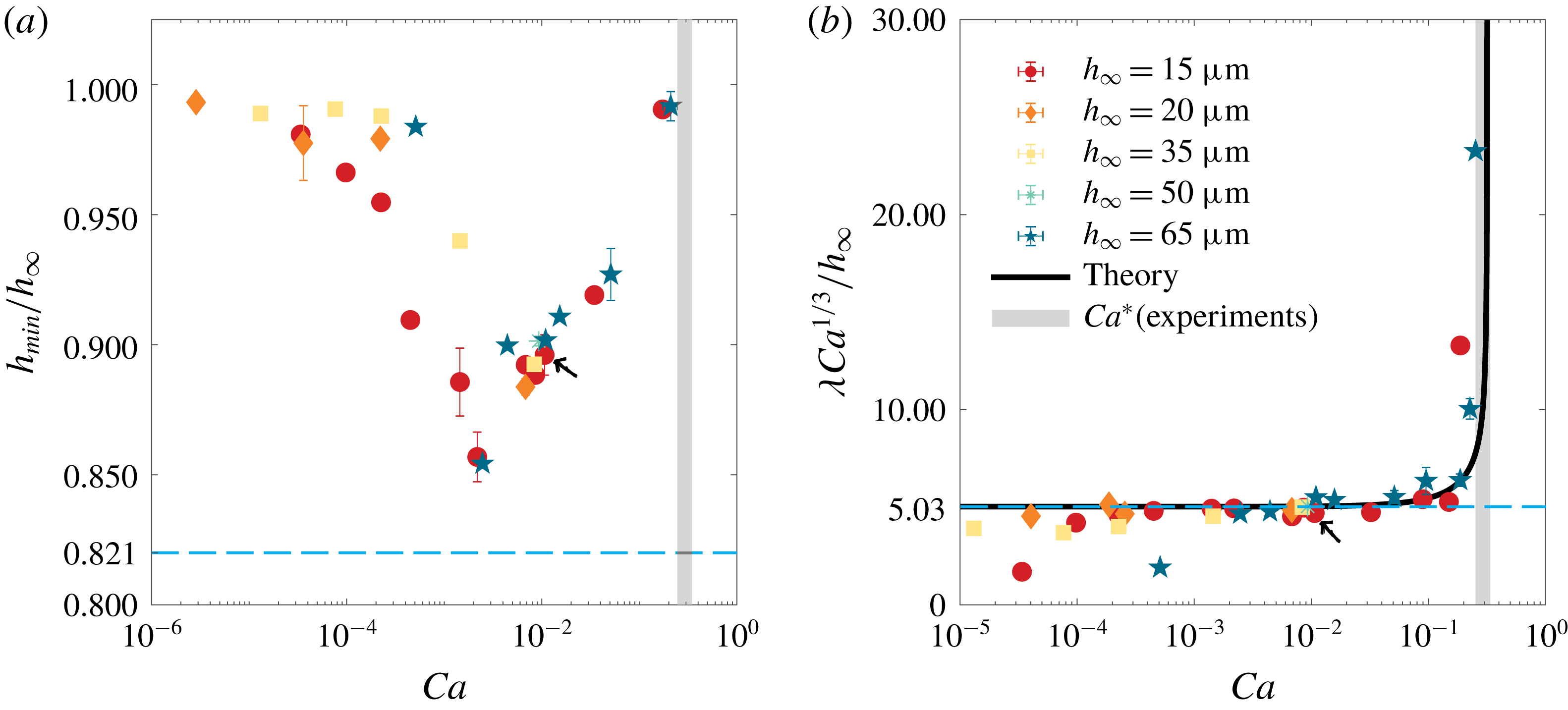
Figure 3. (a) The normalised value of the minimal film thickness $h_{min}/h_{\infty }$ and (b) the normalised wavelength as a function of the capillary number $Ca=\unicode[STIX]{x1D702}v/\unicode[STIX]{x1D6FE}$ . Different symbols correspond to different film thickness $h_{\infty }$ (see legend). The vertical grey regions (determined by statistical error) show the critical $Ca^{\ast }$ beyond which dimples are not observed. The dashed blue lines in (a,b) indicate the asymptotic prediction of lubrication theory without gravity. The solid line in (b) is the prediction of (3.5). For this range of $h_{\infty }$ , the Bond number varies from $Bo=0.0001$ to $Bo=0.0020$ . For the lowest value of $Ca$ , the ratio $Bo/Ca^{2/3}$ is approximately 0.92. The arrows indicate the data points corresponding to the profile shown in figure 1(b). Note that the profile shown in figure 1(c) is obtained for $Ca>Ca^{\ast }$ (the grey vertical line).

The evolution of the wavelength is reported in figure 3(b). The prediction based on linear analysis of lubrication theory without gravity can for example be found in Bretherton (1961), and gives

(2.1) $$\begin{eqnarray}\unicode[STIX]{x1D706}=\frac{4\unicode[STIX]{x03C0}h_{\infty }}{3^{5/6}Ca^{1/3}}\approx 5.03\frac{h_{\infty }}{Ca^{1/3}}.\end{eqnarray}$$

We therefore report our measurement of the wavelength according to $\unicode[STIX]{x1D706}Ca^{1/3}/h_{\infty }$ , as a function of $Ca$ . For small $Ca$ , the rescaled wavelength indeed reaches a constant value ${\approx}5$ , in excellent agreement with (2.1). Interestingly, the rescaled wavelength suddenly diverges when $Ca$ approaches the critical value of $Ca\approx 0.295\pm 0.042$ , at the point where the dimples disappear. Clearly, this feature is not covered by the lubrication result (2.1), predicting a constant value. This may seem somewhat counterintuitive, since the lubrication equation is usually more accurate when waves are longer. However, one should bear in mind that the thin-film equation results from an expansion $Ca\ll 1$ (Oron, Davis & Bankoff 1997). The diverging wavelength in figure 3(b) appears at relatively large velocities, where $Ca$ can no longer be considered asymptotically small. Qualitatively, a capillary number of order unity corresponds to the condition when the speed of the advancing contact line and the growth rate of a ripple are comparable, and therefore the dimples do not have enough time to grow.

3 Linear analysis of the ripples

3.1 Interpretation

We now interpret these experimental observations from the equations of Stokes flow. As far as we are aware, the non-monotonic behaviour of the dimple amplitude was not previously predicted. Here, we remark that, in general, $h_{min}$ cannot be predicted in a closed-form analytical expression. For example, the value $h_{min}/h_{\infty }\approx 0.82$ was obtained by a numerical solution of the lubrication equation, matching to a large drop in the absence of gravity. However, such a lubrication calculation is clearly not applicable at large speeds, where $Ca$ approaches values of order unity. Hence, predicting $h_{min}$ will require full numerical resolution of Stokes flow.

By contrast, explicit predictions for the wavelength $\unicode[STIX]{x1D706}$ can be obtained from a linear analysis of the ripples, for arbitrary $Ca$ . Such a linear analysis is indeed suitable, given that the ripples decay exponentially and thus have a small amplitude compared to the film thickness $h_{\infty }$ . Throughout, our theoretical analysis is one-dimensional, i.e. accounting only for the direction normal to the contact line, although the full problem itself is axially symmetric (see e.g. figure 2). However, two different length scales allow for the separation of the large-scale droplet region and the small-scale contact line region. Near the contact line, where the relevant scale is set by the film thickness, the one-dimensional approach is valid, since the curvature of the large-scale droplet is negligible compared to $h_{\infty }$ . The excellent correspondence between theory and experiments in figure 3(b) will confirm the validity of this approach. When applied to lubrication theory without gravity, this leads to (2.1). The linear analysis for finite $Ca$ , without gravity, was carried out by Taroni et al. (2012) for generic free surface inlet and outlet problems in coating flows. In fact, Taroni et al. (2012) identified a critical capillary number $Ca^{\ast }=1/\unicode[STIX]{x03C0}\approx 0.318$ in the dispersion relation – which coincides with the critical values of $Ca$ found in our experiments (the grey regions in figure 3). As we will show below, their analysis is indeed applicable to our experiments.

We furthermore introduce gravity into the theory, to study the possible effects on the ripples at low $Ca$ . This connects to works on withdrawing plates from a bath, where a steeper angle of the plate was predicted to lead to a disappearance of ripples due to the enhanced influence of gravity (Snoeijer et al. 2008). Indeed, we will find that gravity will introduce a second critical velocity: owing to the scaling $\unicode[STIX]{x1D706}\sim Ca^{-1/3}$ implied by (2.1), the wavelengths can indeed approach the capillary length, $\ell _{\unicode[STIX]{x1D6FE}}$ . The crossover to gravitational effects is expected when $\unicode[STIX]{x1D706}\sim \ell _{\unicode[STIX]{x1D6FE}}$ , which, using (2.1), can be inferred from

(3.1) $$\begin{eqnarray}\frac{\unicode[STIX]{x1D706}^{2}}{\ell _{\unicode[STIX]{x1D6FE}}^{2}}\sim \frac{Bo}{Ca^{2/3}},\end{eqnarray}$$

where $Bo=\unicode[STIX]{x1D70C}gh_{\infty }^{2}/\unicode[STIX]{x1D6FE}$ is the Bond number. The ratio $\unicode[STIX]{x1D706}/\ell _{\unicode[STIX]{x1D6FE}}$ can approach unity for the lowest spreading velocities in our experiment. Therefore, we derive the wavelengths of the ripples in the following, for arbitrary $Ca$ and $Bo$ , and will discuss to what extent they apply to our experiment.

3.2 The ripple wavelength at finite $Ca$ and $Bo$

We now compute the ripple wavelength from the perturbation analysis of the Stokes equation (i.e. neglecting inertia), but including gravity. The incompressible velocity is expressed using the streamfunction, $v_{x}=\unicode[STIX]{x2202}\unicode[STIX]{x1D713}/\unicode[STIX]{x2202}y$ and $v_{y}=-\unicode[STIX]{x2202}\unicode[STIX]{x1D713}/\unicode[STIX]{x2202}x$ , while we introduce the generalised pressure $\bar{p}=p+\unicode[STIX]{x1D70C}gy$ to account for gravity. Using the standard approach (Leal 2010), we can split the problem by respectively taking the curl and divergence of the Stokes equation, which leads to

(3.2a,b ) $$\begin{eqnarray}\unicode[STIX]{x1D6FB}^{4}\unicode[STIX]{x1D713}=0\quad \text{and}\quad \unicode[STIX]{x1D6FB}^{2}\bar{p}=0.\end{eqnarray}$$

We describe the ripple as a small perturbation around the flat state. We place ourselves in a reference frame where we move along with the capillary ripple at the edge of the drop, so that the ripple appears as a stationary profile. In this co-moving frame, the liquid flows to the left so that the unperturbed flat state implies $h=h_{\infty }$ , $\unicode[STIX]{x1D713}=-vy$ and $\bar{p}=0$ . The expansion then takes the form

(3.3a-c ) $$\begin{eqnarray}h(x)=h_{\infty }+\unicode[STIX]{x1D716}\text{e}^{-\unicode[STIX]{x1D70E}x},\quad \unicode[STIX]{x1D713}(x,y)=-vy+\unicode[STIX]{x1D716}f(y)\text{e}^{-\unicode[STIX]{x1D70E}x},\quad \bar{p}(x,y)=\unicode[STIX]{x1D716}q(y)\text{e}^{-\unicode[STIX]{x1D70E}x},\end{eqnarray}$$

and subsequently (3.2) implies

(3.4a,b ) $$\begin{eqnarray}f=A\cos (\unicode[STIX]{x1D70E}y)+B\sin (\unicode[STIX]{x1D70E}y)+Cy\cos (\unicode[STIX]{x1D70E}y)+Dy\sin (\unicode[STIX]{x1D70E}y),\quad q=E\cos (\unicode[STIX]{x1D70E}y)+F\sin (\unicode[STIX]{x1D70E}y).\end{eqnarray}$$

Note that by imposing the Stokes equation $\unicode[STIX]{x1D735}\bar{p}=\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}$ , one can express $\{E,F\}$ in terms of $\{C,D\}$ , so that (3.4) only contains four independent constants.

At the solid boundary we impose a no-slip boundary condition $\boldsymbol{u}=-v\boldsymbol{e}_{x}$ , while at the free surface $\boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{n}=0$ . The dynamic boundary condition at the free surface reads $\unicode[STIX]{x1D749}\boldsymbol{\cdot }\boldsymbol{n}=-\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D705}\boldsymbol{n}$ , where $\unicode[STIX]{x1D705}$ is the (linearised) interface curvature. Finally, the stress can be written as $\unicode[STIX]{x1D749}=-(\bar{p}-\unicode[STIX]{x1D70C}gy)\boldsymbol{I}+\unicode[STIX]{x1D702}(\unicode[STIX]{x1D735}\boldsymbol{u}+(\unicode[STIX]{x1D735}\boldsymbol{u})^{\text{T}})$ . These are five boundary conditions, which, after linearisation, constitute a problem for the four independent coefficients of (3.4). A non-trivial solution arises when satisfying the conditions

(3.5) $$\begin{eqnarray}2Ca(\cos ^{2}\bar{\unicode[STIX]{x1D70E}}-\bar{\unicode[STIX]{x1D70E}}^{2})+(1-\bar{\unicode[STIX]{x1D70E}}^{-2}Bo)(\bar{\unicode[STIX]{x1D70E}}-\sin \bar{\unicode[STIX]{x1D70E}}\cos \bar{\unicode[STIX]{x1D70E}})=0,\end{eqnarray}$$

where we introduced $\bar{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D70E}h_{\infty }$ . For $Bo=0$ , one recovers the result of Taroni et al. (2012), where further details of the calculation can be found.

The wavelength of the ripples is encoded in the roots $\bar{\unicode[STIX]{x1D70E}}$ of (3.5). The imaginary part $\text{Im}(\bar{\unicode[STIX]{x1D70E}})$ provides the wavenumber of the ripple, while the real part $\text{Re}(\bar{\unicode[STIX]{x1D70E}})>0$ describes the decay towards the prewetted film. We therefore visualise the location of the roots in the complex plane, and track their ‘migration’ upon varying the parameters $Ca$ and $Bo$ .

Figure 4(a) shows the roots for increasing $Ca$ when $Bo=0$ . At small $Ca$ , the roots behave as expected from the lubrication limit. Three roots emanate from the origin, two of which have $\text{Re}(\bar{\unicode[STIX]{x1D70E}})>0$ . These provide the oscillations as given by (2.1). At larger $Ca$ , however, the two roots with $\text{Re}(\bar{\unicode[STIX]{x1D70E}})>0$ return to the real axis and merge at the point indicated by the red circle in figure 4(a). This occurs at a critical capillary number $Ca^{\ast }=1/\unicode[STIX]{x03C0}$ , at which $\text{Im}(\bar{\unicode[STIX]{x1D70E}})=0$ for all three roots. For $Ca>Ca^{\ast }$ the third root dominates over the two discussed up until now. This third root has the smallest $\text{Re}(\bar{\unicode[STIX]{x1D70E}})$ of the three roots, which means that it has the slowest decay and is thus the asymptotic solution. Since this root has $\text{Im}(\bar{\unicode[STIX]{x1D70E}})=0$ , a solution without undulation remains. As the critical $Ca^{\ast }$ is approached from below, the wavelength diverges asymptotically as $\unicode[STIX]{x1D706}/h_{\infty }\sim 1/(Ca^{\ast }-Ca)^{1/3}$ , as already reported by Taroni et al. (2012). In fact, the prediction (3.5) provides an excellent description of the experimental data for the ripple wavelength (figure 3 b, solid line). The diverging wavelength indeed coincides with $h_{min}/h_{\infty }\rightarrow 1$ observed experimentally. Hence, the disappearance of the ripples at $Ca^{\ast }$ is due to the appearance of a critical point – a feature that is not present in lubrication theory. Note, that the excellent agreement between the theories and the experimental results also confirms the assumption of quasi-steady dynamics.

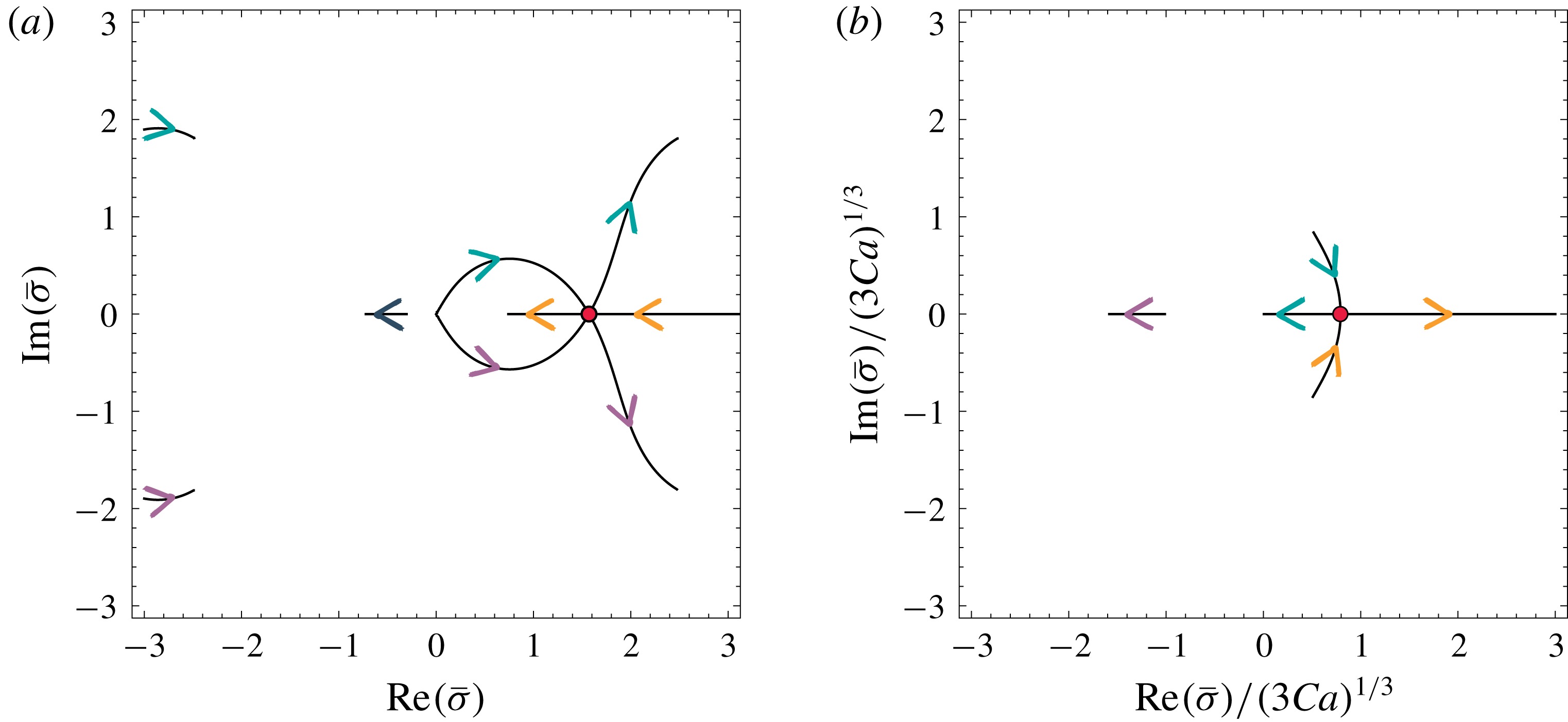
Figure 4. (a) The path of complex roots of (3.5), where $Bo=0$ . Arrows show the migration of the roots on increasing the values of $Ca$ . The red circle corresponds to $Ca=Ca^{\ast }$ . (b) The path of complex roots in the lubrication limit, from (3.6). Arrows show the migration of the roots on increasing the values of $Bo$ . The red circle denotes $Bo=Bo^{\ast }$ .

We now turn to the case of small $Ca$ , for which gravity starts to play a role. In this regime, $|\bar{\unicode[STIX]{x1D70E}}|\ll 1$ , and (3.5) reduces to

(3.6) $$\begin{eqnarray}\bar{\unicode[STIX]{x1D70E}}^{3}=-3Ca+\bar{\unicode[STIX]{x1D70E}}Bo,\end{eqnarray}$$

which is essentially the lubrication limit. There are now three roots for all parameters. Figure 4(b) shows the migration of these roots as we increase the Bond number (the axes are rescaled according to (3.1)). Similar to what was previously observed, the two relevant roots migrate towards the real axis, as $Bo$ is increased. The two ripple solutions disappear via a pitchfork bifurcation at $Bo^{\ast }=2^{-(2/3)}Ca^{2/3}\approx 0.63Ca^{2/3}$ , indicated by the red circle in figure 4(b). This predicts again a diverging wavelength, now in the very small $Ca$ regime, for which $Bo^{\ast }$ becomes sufficiently small. The scaling near the critical point is $\unicode[STIX]{x1D706}/h_{\infty }\sim Ca^{1/3}/(Bo^{\ast }-Bo)^{1/2}$ , as is typical near a pitchfork bifurcation.

The experiments at small $Ca$ reveal $h_{min}/h_{\infty }\rightarrow 1$ , and hence a disappearance of the ripples. We, nonetheless, cannot experimentally confirm the divergence of the wavelength in this limit (cf. figure 3 b), even though at the lowest $Ca$ we are near the critical $Bo$ . As the spreading velocity falls, the ripples become flatter, and the wavelength increases. Therefore, the measurements become more challenging. Besides the effect of gravity, we also suspect that $h_{min}/h_{\infty }\rightarrow 1$ is a finite size effect. Namely, the low velocities are reached in the final stages of the spreading experiments, where the height of the droplet becomes comparable with the thickness of the film. Hence, we loose the separation of scales between the inner (‘contact line’) and outer (droplet) regions (see also Cormier et al. (2012) and Pedersen et al. (2019)). For the smallest $Ca$ in our experiment, we indeed estimated that the drop height above the film thickness is comparable to $h_{\infty }$ , clearly showing a violation of length-scale separation. This lack of scale separation also provides an explanation for why our experiments do approach the asymptotic value $h_{\min }/h_{\infty }\approx 0.82$ predicted by Tuck & Schwartz (1990), but always remain slightly above. A full numerical solution of the governing equations (Stokes equation or lubrication limit) accounting for the finite size and gravity effects is a subject of future study.

4 Conclusions

In this paper, we systematically explored the shape of capillary ripples in a thin oil film when a droplet of the same liquid spreads over the surface. Using a reflective digital holographic microscope, we could measure the microscale features of the thin film. Unexpectedly, we found that the amplitude of the ripple increases, reaches a maximum around $Ca\approx 2\times 10^{-3}$ and then decreases at larger capillary numbers. Above $Ca\approx 0.3$ the dimples completely disappear, in excellent agreement with the linear analysis by Taroni et al. (2012), predicting a critical capillary number $Ca^{\ast }=1/\unicode[STIX]{x03C0}$ . Atypically for thin-film flows, these features cannot be explained by the lubrication approximation. Since surface tension is responsible for the ripples, one can on a qualitative level understand that ripples disappear at large $Ca$ , for which the relative importance of surface tension is diminished. A quantitative analysis shows that the critical point gives a diverging wavelength $\unicode[STIX]{x1D706}\sim 1/(Ca^{\ast }-Ca)^{1/3}$ , a scenario that is for the first time reported experimentally.

For small $Ca$ , our results highlight the possible importance of the length-scale separation as well as gravity, as the height of the drop becomes comparable to the film thickness and the wavelength of the ripples becomes close to the capillary length. These effects can be of great importance for experiments where the structure of the dimples is used to identify rheological fingerprints (Jacobs et al. 1998; Bäumchen & Jacobs 2010). From a more general perspective, the experimental method used, DHM, proves to be a powerful tool for the visualisation of surface profiles of thin films in real time with height resolution that goes down to the nanometre scale. The methodology can be used in further investigations of films on complex topographies or of fluids with more complex rheology (Jalaal & Balmforth 2016; Laborie et al. 2017; Xu & Jensen 2017; Jalaal et al. 2018).