Buoyancy effects in a wall jet over a heated horizontal plate

Abstract

A similarity solution of the boundary layer equations for a wall jet on a heated horizontal surface at constant temperature taking into account the coupling of the temperature and velocity fields by buoyancy is described. This similarity solution exists for any value of 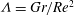${\it\Lambda}=Gr/Re^{2}$, characterizing this coupling between natural and forced convection over the horizontal plate, where 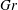$Gr$ is a Grashof number and 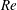$Re$ is a Reynolds number, provided that the plate temperature is higher than the ambient temperature (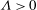${\it\Lambda}>0$, say). Two main qualitative differences are found in the flow structure in relation to the well-known Glauert’s similarity solution for a wall jet without natural convection effects (i.e. when 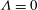${\it\Lambda}=0$): the first is that the similarity variable and structure of the horizontal velocity and temperature have the same functional form for both a radially spreading jet and a two-dimensional jet; the second is that the maximum of the horizontal velocity increases as the jet spreads over the surface, instead of decreasing like in Glauert’s solution, as the radial or horizontal distance to the power 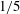$1/5$. To check this similarity solution we solve numerically the boundary layer equations for the particular case of a jet with constant velocity and temperature emerging from a slot of height 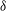${\it\delta}$ and radius 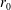$r_{0}$ (in the radially spreading case). An approximate, analytical similarity solution near the jet exit is also found that helps to start the numerical integration. Far from the jet exit the numerical solution tends to the similarity solution for any set of values of the non-dimensional parameters governing the problem, provided that the plate is heated (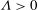${\it\Lambda}>0$). No similarity solution is found numerically for the case of a cooled plate (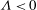${\it\Lambda}<0$). For 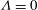${\it\Lambda}=0$ Glauert’s similarity solution is recovered.