Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2025-01-04T04:16:35.005Z Has data issue: false hasContentIssue false
  • English
  • Français

Bifurcation of nonlinear Tollmien–Schlichting waves in a high-speed channel flow

Published online by Cambridge University Press:  16 March 2018

Kengo Deguchi Open the ORCID record for Kengo Deguchi [Opens in a new window]  and
Andrew Walton
Kengo Deguchi*
Affiliation:
School of Mathematical Sciences, Monash University, Victoria 3800, Australia
Andrew Walton
Affiliation:
Department of Mathematics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Plane Poiseuille flow has long served as the simplest testing ground for Tollmien–Schlichting wave instability. In this paper, we provide a comprehensive comparison of equilibrium Tollmien–Schlichting wave solutions arising from new high-resolution Navier–Stokes calculations and the corresponding predictions of various large-Reynolds-number asymptotic theories developed in the last century, such as double-deck theory, viscous nonlinear critical layer theory and strongly nonlinear critical layer theory. In the relatively small to moderate amplitude regime, the theories excellently predict the behaviour of the numerical solutions at Reynolds numbers of order 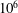$10^{6}$ and above, whilst for larger amplitudes our computations suggest the need for further asymptotic theories to be developed.

JFM classification

Nonlinear Dynamical Systems: Bifurcation Aerodynamics: High-speed flow Instability: Instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 843 , 25 May 2018 , pp. 53 - 97
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1956 On steady laminar flow with closed streamlines at large Reynolds number. J. Fluid Mech. 1, 177–190.Google Scholar
Bennett, J., Hall, P. & Smith, F. T. 1991 The strong nonlinear interaction of Tollmien–Schlichting waves and Taylor–Görtler vortices in curved pipe flow. J. Fluid Mech. 223, 475–495.Google Scholar
Benney, D. J. & Bergeron, R. F. 1969 A new class of nonlinear waves in parallel flows. Stud. Appl. Maths 48, 181–204.10.1002/sapm1969483181Google Scholar
Bodonyi, R. J., Smith, F. T. & Gajjar, J. 1983 Amplitude-dependent stability of boundary layer flow with a strongly nonlinear critical layer. IMA J. Appl. Maths 30, 1–19.Google Scholar
Brown, S. N. & Stewartson, K. 1978 The evolution of a critical layer of a Rossby wave, II. Geophys. Astrophys. Fluid Dyn. 10, 1–24.Google Scholar
Chen, T. S. & Joseph, D. D. 1973 Subcritical bifurcation of plane Poiseuille flow. J. Fluid Mech. 58, 337–351.10.1017/S0022112073002624Google Scholar
Davis, R. E. 1969 On the high Reynolds number flow over a wavy boundary. J. Fluid Mech. 36, 337–346.Google Scholar
Deguchi, K. 2015 Self-sustained states at Kolmogorov microscale. J. Fluid Mech. 781, R6.Google Scholar
Deguchi, K. & Hall, P. 2014a Free-stream coherent structures in parallel boundary-layer flows. J. Fluid Mech. 752, 602–625.Google Scholar
Deguchi, K. & Hall, P. 2014b The high-Reynolds-number asymptotic development of nonlinear equilibrium states in plane Couette flow. J. Fluid Mech. 750, 99–112.Google Scholar
Deguchi, K., Hall, P. & Walton, A. G. 2013 The emergence of localized vortex–wave interaction states in plane Couette flow. J. Fluid Mech. 721, 58–85.Google Scholar
Deguchi, K. & Walton, A. G. 2013a Axisymmetric travelling waves in annular sliding Couette flow at finite and asymptotically large Reynolds number. J. Fluid Mech. 720, 582–617.Google Scholar
Deguchi, K. & Walton, A. G. 2013b A swirling spiral wave solution in pipe flow. J. Fluid Mech. 737, R2.Google Scholar
Dempsey, L. J., Deguchi, K., Hall, P. & Walton, A. G. 2016 Localized vortex/Tollmien–Schlichting wave interaction states in plane Poiseuille flow. J. Fluid Mech. 791, 97–121.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Grohne, D.1969 Die Stabilität der ebenen Kanalstromung gegenüber dreidimensionalen Störungen von endlicher Amplitude. AVA Gottingen, Rep. 69 A 30.Google Scholar
Haberman, R. 1972 Critical layers in parallel flows. Stud. Appl. Maths 51, 139–161.Google Scholar
Haberman, R. 1976 Nonlinear perturbations of the Orr–Sommerfeld equation – asymptotic expansion of the logarithmic phase shift across the critical layer. SIAM J. Math. Anal. 7 (1), 70–81.Google Scholar
Hall, P. 1995 A phase-equation approach to boundary-layer instability theory: Tollmien–Schlichting waves. J. Fluid Mech. 304, 185–212.10.1017/S0022112095004393Google Scholar
Hall, P. & Sherwin, S. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.Google Scholar
Hall, P. & Smith, F. T. 1982 A suggested mechanism for nonlinear wall roughness effects on high Reynolds number flow stability. Stud. Appl. Maths 66, 241–265.Google Scholar
Hall, P. & Smith, F. T. 1991 On strongly nonlinear vortex/wave interactions in boundary-layer transition. J. Fluid Mech. 227, 641–666.Google Scholar
Heisenberg, W. 1924 Über Stabilität und Turbulenz von Flüssigkeitsströmen. Ann. Phys. 379, 577–627.10.1002/andp.19243791502Google Scholar
Herbert, T. 1976 Periodic secondary motions in a plane channel. In Proceedings of the 5th International Conference on Numerical Methods in Fluid Dynamics (ed. Van de Vooren, A. I. & Zandbergen, P. J.), vol. 59, pp. 235–240. Springer.Google Scholar
Itoh, N. 1974 Spatial growth of finite wave disturbances in parallel and nearly parallel flows. Part 1. The theoretical analysis and the numerical results for plane Poiseuille flow. Trans. Japan Soc. Aeronaught. Space Sci. 17, 160–174.Google Scholar
Jimenez, J. 1990 Transition to turbulence in two-dimensional Poiseuille flow. J. Fluid Mech. 218, 265–297.Google Scholar
Kawahara, G., Uhlmann, M. & van Veen, L. 2012 The significance of simple invariant solutions in turbulent flows. Annu. Rev. Fluid Mech. 44, 203–225.Google Scholar
Lin, C. C. 1945 On the stability of two-dimensional parallel flows. Part III – Stability in a viscous fluid. Q. Appl. Maths 3, 277–301.Google Scholar
Lin, C. C. 1955 The theory of Hydrodynamic Stability. Cambridge University Press.Google Scholar
Mellibovsky, F. & Meseguer, A. 2015 A mechanism for streamwise localisation of nonlinear waves in shear flows. J. Fluid Mech. 779, R1.Google Scholar
Milinazzo, F. A. & Saffman, P. G. 1985 Finite-amplitude steady waves in plane viscous shear flows. J. Fluid Mech. 160, 281–295.Google Scholar
Nishioka, M., Iida, S. & Ichikawa, Y. 1975 An experimental investigation of the stability of plane Couette flow. J. Fluid Mech. 72 (4), 731–751.Google Scholar
Orszag, S. A. 1971 Accurate solution of the Orr–Sommerfeld stability equation. J. Fluid Mech. 50, 689–703.Google Scholar
Price, T., Brachet, M. & Pomeau, Y. 1993 Numerical characterization of localised solutions in plane Poiseuille flow. Phys. Fluids A5, 762–764.10.1063/1.858659Google Scholar
Reid, W. H. 1965 The stability of parallel flows. In Basic Developments in Fluid Dynamics (ed. Holt, M.), vol. 1, pp. 249–307. Academic Press.Google Scholar
Schlichting, H. 1933 Laminare Strahlenausbreitung. Z. Angew. Math. Mech. 13, 260–263.Google Scholar
Smith, F. T. 1979a Nonlinear stability of boundary layers for disturbances of various sizes. Proc. R. Soc. Lond. A 368, 573–589; see also Corrections to Nonlinear stability of boundary layers for disturbances of various sizes. Proc. R. Soc. Lond. A 371 439–440.Google Scholar
Smith, F. T. 1979b Instability of flow through pipes of general cross-section, Part 1. Mathematika 26, 187–210.10.1112/S0025579300009761Google Scholar
Smith, F. T. & Bodonyi, R. J. 1982a Nonlinear critical layers and their development in streaming-flow instability. J. Fluid Mech. 118, 165–185.Google Scholar
Smith, F. T. & Bodonyi, R. J. 1982b Amplitude-dependent neutral modes in the Hagen–Poiseuille flow through a circular pipe. Proc. R. Soc. Lond. A 384, 463–489.Google Scholar
Smith, F. T. & Burggraf, O. R. 1985 On the development of large-sized short-scaled disturbances in boundary layers. Proc. R. Soc. Lond. A 399, 25–55.Google Scholar
Smith, F. T., Doorly, D. J. & Rothmayer, A. P. 1990 On displacement-thickness, wall-layer and mid-flow scales in turbulent boundary layers, and slugs of vorticity in channel and pipe flows. Proc. R. Soc. Lond. A 428, 255–281.Google Scholar
Smith, F. T. & Walton, A. G. 1998 Flow past a two- or three-dimensional steep-edged roughness. Proc. R. Soc. Lond. A 454, 31–69.Google Scholar
Stuart, J. T. 1960 On the nonlinear mechanics of wave disturbances in stable and unstable parallel flows. Part 1. The basic behaviour in plane Poiseuille flow. J. Fluid Mech. 9, 353–370.Google Scholar
Tollmien, W. 1929 Uber die Entstehung der Turbulenz. Nachr. Ges. Wiss. Gottingen Math-Phys. Kl. II 21–44.Google Scholar
Waleffe, F. 1997 On a self-sustaining process in shear flows. Phys. Fluids 9, 883–900.Google Scholar
Walton, A. G. 2003 The nonlinear instability of thread-annular flow at high Reynolds number. J. Fluid Mech. 477, 227–257.Google Scholar
Zahn, J.-P., Toomre, J., Spiegel, E. A. & Gough, D. O. 1974 Nonlinear cellular motions in Poiseuille channel flow. J. Fluid Mech. 64, 319–345.Google Scholar