Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-01T03:43:11.085Z Has data issue: false hasContentIssue false
  • English
  • Français

Available potential energy density for Boussinesq fluid flow

Published online by Cambridge University Press:  02 January 2013

Kraig B. Winters  and
Roy Barkan
Kraig B. Winters*
Affiliation:
Scripps Institution of Oceanography, University of California San Diego, La Jolla, CA 92093, USA Mechanical and Aerospace Engineering, University of California San Diego, La Jolla CA 92093-0209, USA
Roy Barkan
Affiliation:
Scripps Institution of Oceanography, University of California San Diego, La Jolla, CA 92093, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

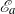An exact expression ${\mathscr{E}}_{a} $ for available potential energy density in Boussinesq fluid flows (Roullet & Klein, J. Fluid Mech., vol. 624, 2009, pp. 45–55; Holliday & McIntyre, J. Fluid Mech., vol. 107, 1981, pp. 221–225) is shown explicitly to integrate to the available potential energy 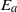${E}_{a} $ of Winters et al. (J. Fluid Mech., vol. 289, 1995, pp. 115–128). 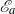${\mathscr{E}}_{a} $ is a positive definite function of position and time consisting of two terms. The first, which is simply the indefinitely signed integrand in the Winters et al. definition of 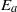${E}_{a} $, quantifies the expenditure or release of potential energy in the relocation of individual fluid parcels to their equilibrium height. When integrated over all parcels, this term yields the total available potential energy 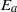${E}_{a} $. The second term describes the energetic consequences of the compensatory displacements necessary under the Boussinesq approximation to conserve vertical volume flux with each parcel relocation. On a pointwise basis, this term adds to the first in such a way that a positive definite contribution to 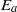${E}_{a} $ is guaranteed. Globally, however, the second term vanishes when integrated over all fluid parcels and therefore contributes nothing to 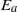${E}_{a} $. In effect, it filters the components of the first term that cancel upon integration, isolating the positive definite residuals. 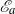${\mathscr{E}}_{a} $ can be used to construct spatial maps of local contributions to 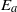${E}_{a} $ for direct numerical simulations of density stratified flows. Because 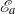${\mathscr{E}}_{a} $ integrates to 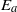${E}_{a} $, these maps are explicitly connected to known, exact, temporal evolution equations for kinetic, available and background potential energies.

JFM classification

Geophysical and Geological Flows: Baroclinic flows Mathematical Foundations: Computational methods Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 714 , 10 January 2013 , pp. 476 - 488
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barkan, R., Winters, K. B. & Llewellyn-Smith, S. G. 2012 Rotating horizontal convection. J. Fluid Mech. (submitted).Google Scholar
Eady, E. 1949 Long waves and cyclone waves. Tellus 1, 33–52.Google Scholar
Holliday, D. & McIntyre, M. E. 1981 On potential energy density in an incompressible, stratified fluid. J. Fluid Mech. 107, 221–225.CrossRefGoogle Scholar
Hughes, G. O. & Griffiths, R. W. 2008 Horizontal convection. Annu. Rev. Fluid Mech. 40, 185–208.CrossRefGoogle Scholar
Hughes, G. O., Hogg, A. M. & Griffiths, R. W. 2009 Available potential energy and irreversible mixing in the meridional overturning circulation. J. Phys. Oceanogr. 39, 3130–3146.CrossRefGoogle Scholar
Lorenz, E. N. 1955 Available potential energy and the maintenance of the general circulation. Tellus 7, 157–167.CrossRefGoogle Scholar
Molemaker, M. J. & McWilliams, J. C. 2010 Local balance and cross-scale flux of available potential energy. J. Fluid Mech. 645, 295–314.CrossRefGoogle Scholar
Roullet, G. & Klein, P. 2009 Available potential energy diagnosis in a direct numerical simulation of rotating stratified turbulence. J. Fluid Mech. 624, 45–55.Google Scholar
Stewart, K. D. 2012 The effect of sills and mixing on the meridional overturning circulation. PhD thesis, Australian National University (in press).Google Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density stratified fluids. J. Fluid Mech. 289, 115–128.CrossRefGoogle Scholar
Winters, K. B. & Young, W. R. 2009 Available potential energy and buoyancy variance in horizontal convection. J. Fluid Mech. 629, 221–230.CrossRefGoogle Scholar
Wood, R. B. & McIntyre, M. E. 2010 A general theorem on angular-momentum changes due to potential vorticity mixing and on potential-energy changes due to buoyancy mixing. J. Atmos. Sci. 67, 1261–1273.Google Scholar