Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T21:29:32.787Z Has data issue: false hasContentIssue false
  • English
  • Français

An unexpected balance between outer Rayleigh streaming sources

Published online by Cambridge University Press:  02 April 2019

D. Baltean-Carlès ,
V. Daru ,
C. Weisman Open the ORCID record for C. Weisman [Opens in a new window] ,
S. Tabakova  and
H. Bailliet
D. Baltean-Carlès
Affiliation:
Sorbonne-Université, Faculté des Sciences et Ingénierie, UFR d’Ingénierie, 4 Place Jussieu, 75005 Paris, France LIMSI, CNRS, Université Paris-Saclay, Bât. 508, Rue John Von Neumann, Campus Universitaire, F-91405 Orsay CEDEX, France
V. Daru
Affiliation:
DynFluid Lab., ENSAM, 151 boulevard de l’hôpital, 75013, Paris, France LIMSI, CNRS, Université Paris-Saclay, Bât. 508, Rue John Von Neumann, Campus Universitaire, F-91405 Orsay CEDEX, France
C. Weisman*
Affiliation:
Sorbonne-Université, Faculté des Sciences et Ingénierie, UFR d’Ingénierie, 4 Place Jussieu, 75005 Paris, France LIMSI, CNRS, Université Paris-Saclay, Bât. 508, Rue John Von Neumann, Campus Universitaire, F-91405 Orsay CEDEX, France
S. Tabakova
Affiliation:
Institute of Mechanics, BAS, 4 acad. G. Bontchev, 1113 Sofia, Bulgaria
H. Bailliet
Affiliation:
Institut Pprime, CNRS - Université de Poitiers - ISAE-ENSMA, ENSIP, 6 Rue Marcel Doré, Bâtiment B17 - BP 633, 86022 Poitiers CEDEX, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Acoustic streaming generated by a plane standing wave between two infinite plates or inside a cylindrical tube is considered, under the isentropic flow assumption. A two-dimensional analysis is performed in the linear case of slow streaming motion, based on analytical formal solutions of separate problems, each associated with a specific source term (Reynolds stress term). In order to obtain these analytical solutions, a necessary geometrical hypothesis is that 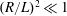$(R/L)^{2}\ll 1$, where 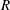$R$ and 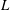$L$ are the guide half-width (or radius) and length. The effect of the two source terms classically taken into account is quantified in order to derive the dependence of the maximum axial streaming velocity on the axis as a function of the ratio 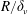$R/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$, where 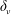$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D708}}$ is the acoustic boundary layer thickness. The effect of two other source terms that are usually neglected, is then analysed. It is found that one of these terms can generate a counter-rotating streaming flow. While negligible for very narrow guides, this term can become important for some values of the aspect ratio $L/R$.

JFM classification

Acoustics: Acoustics Boundary Layers: Boundary Layers Low-Reynolds-number flows: Low-Reynolds-number flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 867 , 25 May 2019 , pp. 985 - 1011
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amari, M., Gusev, V. & Joly, N. 2003 Temporal dynamics of the sound wind in acoustitron. Acta Acust. united with Acustica 89, 1008–1024.Google Scholar
Bailliet, H., Gusev, V., Raspet, R. & Hiller, R. A. 2001 Acoustic streaming in closed thermoacoustic devices. J. Acoust. Soc. Am. 110, 1808–1821.Google Scholar
Boluriaan, S. & Morris, P. J. 2003 Acoustic streaming: from Rayleigh to today. Intl J. Aeroacoust. 2 (3–4), 255–292.Google Scholar
Daru, V., Baltean-Carlès, D., Weisman, C., Debesse, P. & Gandikota, G. 2013 Two-dimensional numerical simulations of nonlinear acoustic streaming in standing waves. Wave Motion 50, 955–963.Google Scholar
Daru, V., Reyt, I., Bailliet, H., Weisman, C. & Baltean-Carlès, D. 2017a Acoustic and streaming velocity components in a resonant wave guide at high acoustic levels. J. Acoust. Soc. Am. 141 (1), 563–574.Google Scholar
Daru, V., Weisman, C., Baltean-Carlès, D., Reyt, I. & Bailliet, H. 2017b Inertial effects on acoustic Rayleigh streaming flow: transient and established regimes. Wave Motion 74, 1–17.Google Scholar
Favre, A. 1965 Équations des gaz turbulents compressibles ii.-méthode des vitesses moyennes; méthode des vitesses macroscopiques pondérées par la masse volumique. J. Méch. 87, 391–421.Google Scholar
Hamilton, M. F., Ilinskii, Y. A. & Zabolotskaya, E. A. 2003a Acoustic streaming generated by standing waves in two-dimensional channels of arbitrary width. J. Acoust. Soc. Am. 113 (1), 153–160.Google Scholar
Hamilton, M. F., Ilinskii, Y. A. & Zabolotskaya, E. A. 2003b Thermal effects on acoustic streaming in standing waves. J. Acoust. Soc. Am. 114 (6), 3092–3101.Google Scholar
Lighthill, J. 1978 Acoustic streaming. J. Sound Vib. 61, 391–418.Google Scholar
Menguy, L. & Gilbert, J. 2000a Non-linear acoustic streaming accompanying a plane stationary wave in a guide. Acta Acust. united with Acustica 86, 249–259.Google Scholar
Menguy, L. & Gilbert, J. 2000b Weakly nonlinear gas oscillations in air-filled tubes; solutions and experiments. Acta Acust. united with Acustica 86 (5), 798–810.Google Scholar
Moreau, S., Bailliet, H. & Valière, J.-C. 2008 Measurements of inner and outer streaming vortices in a standing waveguide using laser doppler velocimetry. J. Acoust. Soc. Am. 123 (2), 640–647.Google Scholar
Nyborg, W. L. 1953 Acoustic streaming due to attenuated plane waves. J. Acoust. Soc. Am. 25, 68–75.Google Scholar
Nyborg, W. L. 1965 Acoustic streaming. In Physical Acoustics (ed. Mason, W. P.), vol. 2B, pp. 265–331. Academic Press.Google Scholar
Olson, J. R. & Swift, G. W. 1997 Acoustic streaming in pulse tube refrigerators: tapered pulse tubes. Cryogenics 37, 769–776.Google Scholar
Paridaens, R., Kouidri, S. & Jebali Jerbi, F. 2013 Investigation on the generation mechanisms of acoustic streaming in a thermoacoustic prime mover. Cryogenics 58, 78–84.Google Scholar
Pierce, A. D. 1989 Acoustics: An Introduction to its Physical Principles and Applications. ASA.Google Scholar
Qi, Q. 1993 The effect of compressibility on acoustic streaming near a rigid boundary for a plane traveling wave. J. Acoust. Soc. Am. 94, 1090–1098.Google Scholar
Rayleigh, Lord 1884 On the circulation of air observed in Kundt tubes, and on some allied acoustical problems. Phil. Trans. R. Soc. Lond. 175, 1–21.Google Scholar
Reyt, I., Daru, V., Bailliet, H., Moreau, S., Valière, J.-C., Baltean-Carlès, D. & Weisman, C. 2013 Fast acoustic streaming in standing waves: generation of an additional outer streaming cell. J. Acoust. Soc. Am. 134, 1791–1801.Google Scholar
Reyt, I., Bailliet, H. & Valière, J.-C. 2014 Experimental investigation of acoustic streaming in a cylindrical wave guide up to high streaming Reynolds numbers. J. Acoust. Soc. Am. 135 (1), 27–37.Google Scholar
Rott, N. 1974 The influence of heat conduction on acoustic streaming. Z. Angew. Math. Phys. 25, 417–421.Google Scholar
Schlichting, H. 1932 Berechnung ebener periodischer Grenzschicht- strommungen [calculation of plane periodic boundary layer streaming]. Phys. Zcit. 33, 327–335.Google Scholar
Schuster, V. K. & Matz, W. 1940 Über stationare Strömungen im Kundtschen Rohr (on stationary streaming in Kundt tubes). Akust. Zh. 5, 349–352.Google Scholar
Sugimoto, N. 2016 Nonlinear theory for thermoacoustic waves in a naroow channel and pore subject to a temperature gradient. J. Fluid Mech. 797, 765–801.Google Scholar
Thompson, M. W., Atchley, A. A. & Maccarone, M. J. 2004 Influences of a temperature gradient and fluid inertia on acoustic streaming in a standing wave. J. Acoust. Soc. Am. 117 (4), 1839–1849.Google Scholar
Waxler, R. 2001 Stationary velocity and pressure gradients in a thermoacoustic stack. J. Acoust. Soc. Am. 109 (6), 2739–2750.Google Scholar
Westervelt, P. J. 1953 The theory of steady rotational flow generated by a sound field. J. Acoust. Soc. Am. 25, 60–67.Google Scholar
Wiklund, M. G., Green, R. & Ohlin, M. 2012 Acoustofluidics 14: applications of acoustic streaming in microfluidic devices. Lab on a Chip 12, 2438–2451.Google Scholar
Wolfram Research Inc.2018 Mathematica, Version 11.3, Champaign, IL.Google Scholar
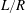Zarembo, L. K. 1971 Acoustic streaming. In High-Intensity Ultrasonic Fields (ed. Rozenberg, L. D.), vol. 175, pp. 135–199. Plenum Press.Google Scholar