Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-12-01T00:48:40.172Z Has data issue: false hasContentIssue false
  • English
  • Français

Weakly nonlinear stability analysis of subcritical electrohydrodynamic flow subject to strong unipolar injection

Published online by Cambridge University Press:  03 March 2016

Mengqi Zhang
Mengqi Zhang*
Affiliation:
Département Fluides, Thermique, Combustion, Institut PPrime, CNRS-Université de Poitiers-ENSMA, UPR 3346, 43 Route de l’Aérodrome, Poitiers CEDEX F86036, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyse in detail the weakly nonlinear stability of electrohydrodynamic (EHD) flow of insulating fluids subject to strong unipolar injection, with and without cross-flow. We first consider the hydrostatic electroconvetion induced by a Coulomb force confined between two infinite flat electrodes, taking into account the charge diffusion effect. The effects of various non-dimensionalized parameters are examined in order to depict in detail and to understand better the subcritical bifurcation of hydrostatic electroconvetion. 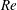In addition, electrohydrodynamics with low- or high-$Re$ cross-flow is also considered for investigating the combined effect of inertia and the electric field. It is found that the base cross-flow is modified by the electric effect and that, even when the inertia is dominating, the electric field can still strengthen effectively the subcritical characteristics of canonical channel flow. In this process, however, the electric field does not contribute directly to the subcriticality of the resultant flow and the intensified subcritical feature of such flow is thus entirely due to the modified hydrodynamic field as a result of the imposed electric field. This finding might be important for flow control strategies involving an electric field. Theoretically, the above results are obtained from a multiple-scale expansion method, which gives rise to the Ginzburg–Landau equation governing the amplitude of the first-order perturbation. The conclusions are deduced by probing the changes of value of the coefficients in this equation. In particular, the sign of the first Landau coefficient indicates the type of bifurcation, being subcritical or supercritical. Moreover, as a quintic-order Ginzburg–Landau equation is derived, the effects of higher-order nonlinear terms in EHD flow are also discussed.

JFM classification

Nonlinear Dynamical Systems: Bifurcation MHD and Electrohydrodynamics: MHD and Electrohydrodynamics Nonlinear Dynamical Systems: Nonlinear Dynamical Systems
Type
Papers
Information
Journal of Fluid Mechanics , Volume 792 , 10 April 2016 , pp. 328 - 363
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atten, P. & Honda, T. 1982 The electroviscous effect and its explanation I – the electrohydrodynamic origin: study under unipolar D.C. injection. J. Electrostat. 11 (3), 225–245.Google Scholar
Atten, P. & Lacroix, J. C. 1974 Stabilité hydrodynamique non-linéaire d’un liquide isolant soumis à une injection unipolaire forte. C. R. Acad. Sci. Paris B 278, 385–387.Google Scholar
Atten, P. & Lacroix, J. C. 1979 Non-linear hydrodynamic stability of liquids subjected to unipolar injection. J. Méc. 18, 469–510.Google Scholar
Atten, P. & Moreau, R. 1972 Stabilité electrohydrodynamique des liquides isolants soumis à une injection unipolaire. J. Méc. 11, 471–520.Google Scholar
Bender, C. M. & Orszag, S. A. 1999 Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory. Springer.CrossRefGoogle Scholar
Boyd, J. P. 2001 Chebyshev and Fourier Spectral Methods, 2nd revised edn. Dover.Google Scholar
Castellanos, A. 1998 Electrohydrodynamics. Springer.Google Scholar
Castellanos, A. & Agrait, N. 1992 Unipolar injection induced instabilities in plane parallel flows. IEEE Trans. Ind. Applics. 28 (3), 513–519.Google Scholar
Castellanos, A., Atten, P. & Perez, A. 1987 Finite amplitude electroconvection in liquids in the case of weak unipolar injection. Physico-Chem. Hydrodyn. 9 (3–4), 443–452.Google Scholar
Castellanos, A., Perez, A. & Atten, P. 1989 Charge diffusion versus coulomb repulsion in finite amplitude electroconvection. In Industry Applications Society Annual Meeting, 1989, Conference Record of the 1989 IEEE, vol. 2, pp. 2112–2117.Google Scholar
Chekila, A., Nouar, C., Plaut, E. & Nemdili, A. 2011 Subcritical bifurcation of shear-thinning plane Poiseuille flows. J. Fluid Mech. 686, 272–298.Google Scholar
Chicón, R., Castellanos, A. & Martin, E. 1997 Numerical modelling of Coulomb-driven convection in insulating liquids. J. Fluid Mech. 344, 43–66.Google Scholar
Cowley, S. J. & Wu, X.1994 Asymptotic approaches to transition modelling. In Progress in Transition Modelling, AGARD Rep. 793.Google Scholar
Craik, A. D. D. 1971 Non-linear resonant instability in boundary layers. J. Fluid Mech. 50, 393–413.Google Scholar
Cross, M. C. 1980 Derivation of the amplitude equation at the Rayleigh–Benard instability. Phys. Fluids 23 (9), 1727–1731.CrossRefGoogle Scholar
Cross, M. C. & Hohenberg, P. C. 1993 Pattern formation outside of equilibrium. Rev. Mod. Phys. 65 (3), 851–1112.CrossRefGoogle Scholar
Davey, A., Hocking, L. M. & Stewartson, K. 1974 On the nonlinear evolution of three-dimensional disturbances in plane Poiseuille flow. J. Fluid Mech. 63, 529–536.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1996 Generalized stability theory. Part I: autonomous operators. J. Atmos. Sci. 53 (14), 2025–2040.Google Scholar
Félici, N. 1971 DC conduction in liquid dielectrics. Part II: electrohydrodynamic phenomena. Direct Current Power Electron. 2, 147–165.Google Scholar
Fujimura, K. 1989 The equivalence between two perturbation methods in weakly nonlinear stability theory for parallel shear flows. Proc. R. Soc. Lond. A 424 (1867), 373–392.Google Scholar
Fujimura, K. 1991 Methods of centre manifold and multiple scales in the theory of weakly nonlinear stability for fluid motions. Proc. R. Soc. Lond. A 434 (1892), 719–733.Google Scholar
Fujimura, K. 1997 Centre manifold reduction and the Stuart–Landau equation for fluid motions. Proc. R. Soc. Lond. A 453 (1956), 181–203.Google Scholar
Fujimura, K. & Kelly, R. E. 1995 Interaction between longitudinal convection rolls and transverse waves in unstably stratified plane Poiseuille flow. Phys. Fluids 7 (1), 68–79.Google Scholar
Gao, Z., Sergent, A., Podvin, B., Xin, S., Le Quéré, P. & Tuckerman, L. S. 2013 Transition to chaos of natural convection between two infinite differentially heated vertical plates. Phys. Rev. E 88, 023010.Google Scholar
Guckenheimer, J. & Holmes, P. 1983 Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, Applied Mathematical Sciences, 42. Springer.Google Scholar
Herbert, T. 1980 Nonlinear stability of parallel flows by high-ordered amplitude expansions. AIAA J. 18 (3), 243–248.Google Scholar
Herbert, T. 1983 On perturbation methods in nonlinear stability theory. J. Fluid Mech. 126, 167–186.Google Scholar
Huerre, P. & Rossi, M. 1998 Hydrodynamic instabilities in open flows. In Hydrodynamics and Nonlinear Instabilities, pp. 81–294. Cambridge University Press.Google Scholar
Kato, Y. & Fujimura, K. 2000 Prediction of pattern selection due to an interaction between longitudinal rolls and transverse modes in a flow through a rectangular channel heated from below. Phys. Rev. E 62, 601–611.Google Scholar
Kolyshkin, A. A. & Ghidaoui, M. S. 2003 Stability analysis of shallow wake flows. J. Fluid Mech. 494, 355–377.Google Scholar
Kramer, L. & Pesch, W. 1995 Convection instabilities in nematic liquid crystals. Annu. Rev. Fluid Mech. 27 (1), 515–539.Google Scholar
Lacroix, J. C., Atten, P. & Hopfinger, E. J. 1975 Electro-convection in a dielectric liquid layer subjected to unipolar injection. J. Fluid Mech. 69 (03), 539–563.Google Scholar
Landau, L. D. 1944 On the problem of turbulence. C. R. Acad. Sci. URSS 44 (31), 1–314.Google Scholar
Lara, J. L., Castellanos, A. & Pontiga, F. 1997 Destabilization of plane Poiseuille flow of insulating liquids by unipolar charge injection. Phys. Fluids 9 (2), 399–406.Google Scholar
Luchini, P. & Bottaro, A. 2014 Adjoint equations in stability analysis. Annu. Rev. Fluid Mech. 46 (1), 493–517.Google Scholar
Mccluskey, F. M. J. & Atten, P. 1988 Modifications to the wake of a wire across Poiseuille flow due to a unipolar space charge. J. Fluid Mech. 197, 81–104.Google Scholar
Melcher, J. R. 1981 Continuum Electromechanics. MIT Press.Google Scholar
Pérez, A. T. & Castellanos, A. 1989 Role of charge diffusion in finite-amplitude electroconvection. Phys. Rev. A 40 (10), 5844–5855.CrossRefGoogle ScholarPubMed
Pesch, W. & Kramer, L. 1986 Nonlinear analysis of spatial structures in two-dimensional anisotropic pattern forming systems. Z. Phys. B 63 (1), 121–130.Google Scholar
Plaut, E., Decker, W., Rossberg, A. G., Kramer, L., Pesch, W., Belaidi, A. & Ribotta, R. 1997 New symmetry breaking in nonlinear electroconvection of nematic liquid crystals. Phys. Rev. Lett. 79, 2367–2370.Google Scholar
Plaut, E., Lebranchu, Y., Simitev, R. & Busse, F. H. 2008 Reynolds stresses and mean fields generated by pure waves: applications to shear flows and convection in a rotating shell. J. Fluid Mech. 602, 303–326.Google Scholar
Reynolds, W. C. & Potter, M. C. 1967 Finite-amplitude instability of parallel shear flows. J. Fluid Mech. 27 (03), 465–492.Google Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.Google Scholar
Schneider, J. M. & Watson, P. K. 1970 Electrohydrodynamic stability of space-charge-limited currents in dielectric liquids. I. Theoretical study. Phys. Fluids 13 (8), 1948–1954.Google Scholar
Sen, P. K. & Venkateswarlu, D. 1983 On the stability of plane Poiseuille flow to finite-amplitude disturbances, considering the higher-order landau coefficients. J. Fluid Mech. 133, 179–206.Google Scholar
Soldati, A. & Banerjee, S. 1998 Turbulence modification by large-scale organized electrohydrodynamic flows. Phys. Fluids 10 (7), 1742–1756.Google Scholar
Stewartson, K. & Stuart, J. T. 1971 A non-linear instability theory for a wave system in plane Poiseuille flow. J. Fluid Mech. 48 (03), 529–545.Google Scholar
Stuart, J. T. 1960 On the non-linear mechanics of wave disturbances in stable and unstable parallel flows. Part 1. The basic behaviour in plane Poiseuille flow. J. Fluid Mech. 9, 353–370.Google Scholar
Traoré, P. & Wu, J. 2013 On the limitation of imposed velocity field strategy for coulomb-driven electroconvection flow simulations. J. Fluid Mech. 727, R3.Google Scholar
Traoré, P. H., Párez, A. T., Koulova, D. & Romat, H. 2010 Numerical modelling of finite-amplitude electro-thermo-convection in a dielectric liquid layer subjected to both unipolar injection and temperature gradient. J. Fluid Mech. 658, 279–293.Google Scholar
Trefethen, L. 2000 Spectral Methods in MATLAB. Society for Industrial and Applied Mathematics.Google Scholar
Trefethen, L. & Embree, M. 2005 Spectra and Pseudospectra: The Behavior of Nonnormal Matrices and Operators. Princeton University Press.Google Scholar
Tuckerman, L. S. & Barkley, D. 1999 Bifurcation analysis of time teppers. In IMA Volumes in Mathematics and Its Applications, pp. 453–466. Springer.Google Scholar
Turnbull, R. J. 1968 Electroconvective instability with a stabilizing temperature gradient. I. Theory. Phys. Fluids 11 (12), 2588–2596.Google Scholar
Watson, J. 1960 On the non-linear mechanics of wave disturbances in stable and unstable parallel flows. Part 2. The development of a solution for plane Poiseuille flow and for plane couette flow. J. Fluid Mech. 9, 371–389.Google Scholar
Weideman, J. A. & Reddy, S. C. 2000 A MATLAB differentiation matrix suite. ACM Trans. Math. Softw. 26 (4), 465–519.Google Scholar
Worraker, W. J. & Richardson, A. T. 1981 A nonlinear electrohydrodynamic stability analysis of a thermally stabilized plane layer of dielectric liquid. J. Fluid Mech. 109, 217–237.Google Scholar
Wu, J., Traoré, P., Pérez, A. T. & Vázquez, P. A. 2015a On two-dimensional finite amplitude electro-convection in a dielectric liquid induced by a strong unipolar injection. J. Electrostat. 74 (0), 85–95.Google Scholar
Wu, J., Traoré, P., Pérez, A. T. & Zhang, M. 2015b Numerical analysis of the subcritical feature of electro-thermo-convection in a plane layer of dielectric liquid. Physica D 311–312, 45–57.Google Scholar
Wu, J., Traoré, P., Vázquez, P. A. & Pérez, A. T. 2013 Onset of convection in a finite two-dimensional container due to unipolar injection of ions. Phys. Rev. E 88 (5), 53018.Google Scholar
Zhang, M., Martinelli, F., Wu, J., Schmid, P. J. & Quadrio, M. 2015 Modal and nonmodal stability analysis of electrohydrodynamic flow with and without cross-flow. J. Fluid Mech. 770, 319–349.Google Scholar