Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
CHAN, I-CHI
and
LIU, PHILIP L.-F.
2009.
Responses of Bingham-plastic muddy seabed to a surface solitary wave.
Journal of Fluid Mechanics,
Vol. 618,
Issue. ,
p.
155.
Huang, Lingyan
and
Chen, Qin
2009.
Spectral Collocation Model for Solitary Wave Attenuation and Mass Transport over Viscous Mud.
Journal of Engineering Mechanics,
Vol. 135,
Issue. 8,
p.
881.
Xia, Yue-Zhang
and
Zhu, Ke-Qin
2010.
A study of wave attenuation over a Maxwell model of a muddy bottom.
Wave Motion,
Vol. 47,
Issue. 8,
p.
601.
PARK, YONG SUNG
and
LIU, PHILIP L.-F.
2010.
Oscillatory pipe flows of a yield-stress fluid.
Journal of Fluid Mechanics,
Vol. 658,
Issue. ,
p.
211.
Xia, YueZhang
and
Zhu, KeQin
2012.
The propagation of a solitary wave over seabed mud of the Voigt model.
Science China Physics, Mechanics and Astronomy,
Vol. 55,
Issue. 1,
p.
108.
Lee, Kwang-Ho
Kim, Dong-Wook
Kang, Gi-Chun
Kim, Do-Sam
Kim, Tae-Hyung
and
Na, Seung-Min
2015.
An Analytical Solution of Dynamic Responses for Seabed under Coexisting Fields of Flow and Partial Standing Wave with Arbitrary Reflection Ratio.
Journal of the Korean Geotechnical Society,
Vol. 31,
Issue. 6,
p.
27.
Wu, Han-Lun
Hsiao, Shih-Chun
Hsu, Wen-Yang
Yang, Ray-Yeng
and
Hwung, Hwung-Hweng
2015.
Dynamic response of density-stratified fluid in a submarine rectangular trench.
Journal of Hydro-environment Research,
Vol. 9,
Issue. 1,
p.
61.
Lee, Kwang-Ho
Kim, Dong-Wook
Kim, Do-Sam
Kim, Tae-Hyung
Kim, Kyu-Han
and
Jeon, Jong-Hyeok
2015.
An Analytical Solution of Dynamic Responses for Seabed under Flow and Standing Wave Coexisting Fields.
Journal of Korean Society of Coastal and Ocean Engineers,
Vol. 27,
Issue. 2,
p.
118.
Le Meur, Hervé V.J.
2015.
Derivation of a viscous Boussinesq system for surface water waves.
Asymptotic Analysis,
Vol. 94,
Issue. 3-4,
p.
309.
Shamsnia, S.
and
Dutykh, Denys
2020.
An Analytical Study on Wave-Current-Mud Interaction.
Water,
Vol. 12,
Issue. 10,
p.
2899.
Tong, L. L.
Zheng, J. H.
Zhang, J. S.
and
Qian, F. S.
2020.
APAC 2019.
p.
65.
Soltanpour, Mohsen
Shamsnia, S. Hadi
Shibayama, Tomoya
and
Nakamura, Ryota
2020.
Experimental and analytical investigation of the response of a mud layer to solitary waves.
Ocean Dynamics,
Vol. 70,
Issue. 2,
p.
165.
Tong, Linlong
Zhang, Jisheng
Zhao, Jialin
Zheng, Jinhai
and
Guo, Yakun
2020.
Modelling study of wave damping over a sandy and a silty bed.
Coastal Engineering,
Vol. 161,
Issue. ,
p.
103756.
Guo, Ronglian
and
Lo, Peter H.-Y.
2022.
Numerical Investigation on Solitary Wave Interaction with a Vertical Cylinder over a Viscous Mud Bed.
Water,
Vol. 14,
Issue. 7,
p.
1135.
Chan, I-Chi
2022.
Theoretical Model for Nonlinear Long Waves over a Thin Viscoelastic Muddy Seabed.
Mathematics,
Vol. 10,
Issue. 15,
p.
2715.
Kostikov, Vasily K.
Hayatdavoodi, Masoud
and
Ertekin, R. Cengiz
2024.
Nonlinear waves propagating over a deformable seafloor.
Physics of Fluids,
Vol. 36,
Issue. 9,
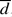 , plays an important role in characterizing mud flow regimes. When
, plays an important role in characterizing mud flow regimes. When 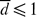 , the vertical profile of the horizontal velocity in the mud bed can be parameterized as a parabola. On the other hand, when
, the vertical profile of the horizontal velocity in the mud bed can be parameterized as a parabola. On the other hand, when 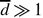 , the velocity profile appears as a plug flow above a thin viscous layer. When
, the velocity profile appears as a plug flow above a thin viscous layer. When 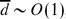 , the flow patterns are more complex than the other two regimes and flow reversal can occur inside the viscous mud bed.
, the flow patterns are more complex than the other two regimes and flow reversal can occur inside the viscous mud bed.