Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
ZHU, LUODING
2008.
Scaling laws for drag of a compliant body in an incompressible viscous flow.
Journal of Fluid Mechanics,
Vol. 607,
Issue. ,
p.
387.
Michelin, Sébastien
and
Llewellyn Smith, Stefan G.
2009.
An unsteady point vortex method for coupled fluid–solid problems.
Theoretical and Computational Fluid Dynamics,
Vol. 23,
Issue. 2,
p.
127.
Zhu, Luoding
He, Guowei
Wang, Shizhao
Miller, Laura
Zhang, Xing
You, Qian
and
Fang, Shiaofen
2011.
An immersed boundary method based on the lattice Boltzmann approach in three dimensions, with application.
Computers & Mathematics with Applications,
Vol. 61,
Issue. 12,
p.
3506.
Shelley, Michael J.
and
Zhang, Jun
2011.
Flapping and Bending Bodies Interacting with Fluid Flows.
Annual Review of Fluid Mechanics,
Vol. 43,
Issue. 1,
p.
449.
Miller, Laura A.
Santhanakrishnan, Arvind
Jones, Shannon
Hamlet, Christina
Mertens, Keith
and
Zhu, Luoding
2012.
Reconfiguration and the reduction of vortex-induced vibrations in broad leaves.
Journal of Experimental Biology,
Vol. 215,
Issue. 15,
p.
2716.
Vahidkhah, Koohyar
and
Abdollahi, Vahid
2012.
Numerical simulation of a flexible fiber deformation in a viscous flow by the immersed boundary-lattice Boltzmann method.
Communications in Nonlinear Science and Numerical Simulation,
Vol. 17,
Issue. 3,
p.
1475.
Stewart, Robert L.
Fox, James F.
and
Harnett, Cindy K.
2013.
Time-Average Velocity and Turbulence Measurement Using Wireless Bend Sensors in an Open Channel with a Rough Bed.
Journal of Hydraulic Engineering,
Vol. 139,
Issue. 7,
p.
696.
Yuan, Hai-Zhuan
Niu, Xiao-Dong
Shu, Shi
Li, Mingjun
and
Yamaguchi, Hiroshi
2014.
A momentum exchange-based immersed boundary-lattice Boltzmann method for simulating a flexible filament in an incompressible flow.
Computers & Mathematics with Applications,
Vol. 67,
Issue. 5,
p.
1039.
Yang, Xiufeng
Liu, Moubin
and
Peng, Shiliu
2014.
Smoothed particle hydrodynamics and element bending group modeling of flexible fibers interacting with viscous fluids.
Physical Review E,
Vol. 90,
Issue. 6,
Allaire, Ryan
Guerron, Pamela
Nita, Bogdan
Nolan, Peter
and
Vaidya, Ashwin
2015.
On the equilibrium configurations of flexible fibers in a flow.
International Journal of Non-Linear Mechanics,
Vol. 69,
Issue. ,
p.
157.
Li, Weiyi
Chen, Kai K.
Wang, Yi-Ning
Krantz, William B.
Fane, Anthony G.
and
Tang, Chuyang Y.
2016.
A conceptual design of spacers with hairy structures for membrane processes.
Journal of Membrane Science,
Vol. 510,
Issue. ,
p.
314.
Zhu, Luoding
Yu, Xijun
Liu, Nansheng
Cheng, Yongguang
and
Lu, Xiyun
2017.
A deformable plate interacting with a non-Newtonian fluid in three dimensions.
Physics of Fluids,
Vol. 29,
Issue. 8,
Nita, Bogdan
and
Allaire, Ryan
2017.
On the Three Dimensional Interaction between Flexible Fibers and Fluid Flow.
Fluids,
Vol. 2,
Issue. 1,
p.
4.
Nita, Bogdan
Nolan, Peter
and
Vaidya, Ashwin
2017.
Numerical study of body shape and wing flexibility in fluid structure interaction.
Computational and Applied Mathematics,
Vol. 36,
Issue. 4,
p.
1733.
Leclercq, T.
Peake, N.
and
de Langre, E.
2018.
Does flutter prevent drag reduction by reconfiguration?.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 474,
Issue. 2209,
p.
20170678.
Liu, Moubin
and
Zhang, Zhilang
2019.
Smoothed particle hydrodynamics (SPH) for modeling fluid-structure interactions.
Science China Physics, Mechanics & Astronomy,
Vol. 62,
Issue. 8,
Huang, Wei-Xi
and
Tian, Fang-Bao
2019.
Recent trends and progress in the immersed boundary method.
Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science,
Vol. 233,
Issue. 23-24,
p.
7617.
Jung, Sung Yong
Kim, Jeong Jae
and
Lee, Sang Joon
2019.
Effect of material stiffness on the motion and flow near the free end of a finite cylinder surface.
Experimental Thermal and Fluid Science,
Vol. 102,
Issue. ,
p.
548.
Bose, Chandan
Sarkar, Sunetra
and
Gupta, Sayan
2020.
Recent Advances in Theoretical, Applied, Computational and Experimental Mechanics.
p.
449.
Zhang, Xiang
He, Guowei
and
Zhang, Xing
2020.
Fluid–structure interactions of single and dual wall-mounted 2D flexible filaments in a laminar boundary layer.
Journal of Fluids and Structures,
Vol. 92,
Issue. ,
p.
102787.
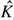 b, and dimensionless fibre length
b, and dimensionless fibre length 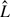 on vortex shedding. According to the simulation results, Re,
on vortex shedding. According to the simulation results, Re, 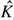 b, and
b, and 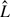 each has a significant influence on the structure of shed vortices. However, Re has little influence on the vortex shedding frequency. With the increase of dimensionless bending modulus, the dimensionless vortex shedding frequency (fvs) and the critical Reynolds number (Rec) decrease approximately as power-law functions. Both fvs and Rec increase approximately linearly as dimensionless fibre length increases.
each has a significant influence on the structure of shed vortices. However, Re has little influence on the vortex shedding frequency. With the increase of dimensionless bending modulus, the dimensionless vortex shedding frequency (fvs) and the critical Reynolds number (Rec) decrease approximately as power-law functions. Both fvs and Rec increase approximately linearly as dimensionless fibre length increases.